An object kept near a convex lens of focal length f, executes SHM between P and Q according to the equation y=Asinωt, O being the mean position. Take x-axis as the principal axis of the lens and A<<D to answer the following questions:
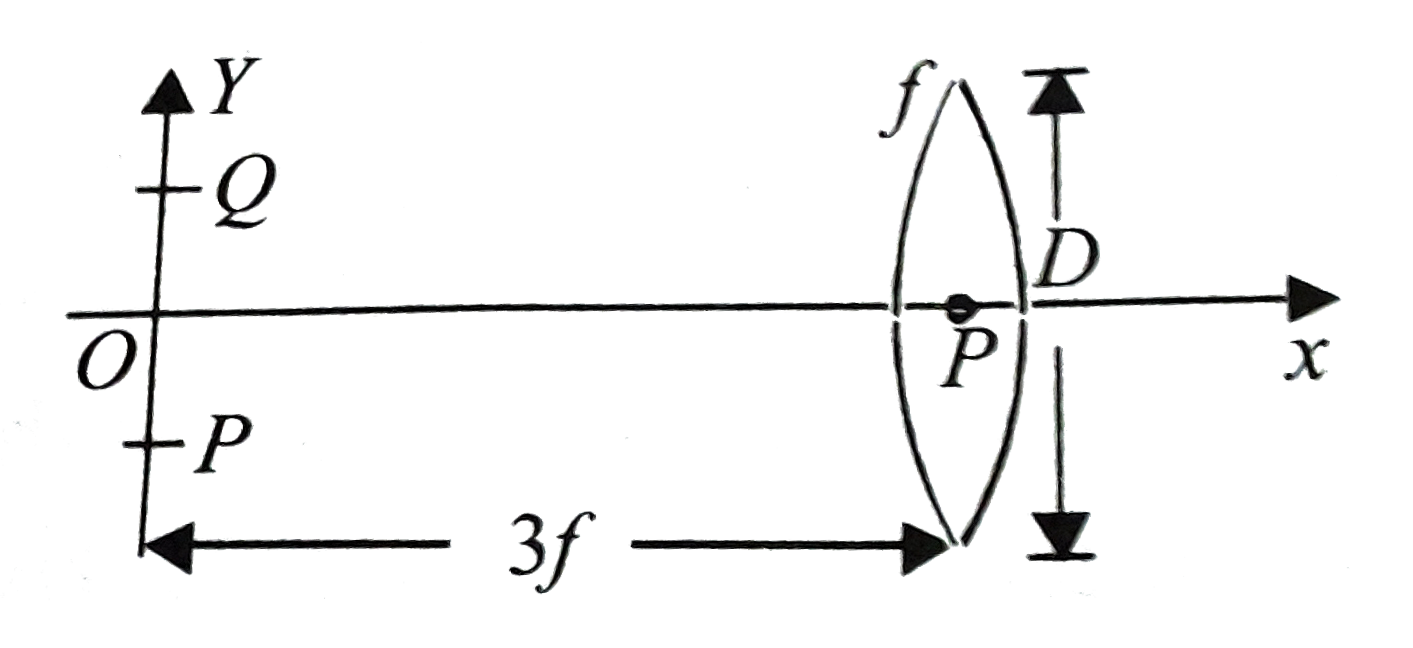
Q. The amplitude of oscillation of the image is
Amplitude of oscillation of its image is 2A
Amplitude of oscillations of its image is A2
Phase difference between the object and its image is π.
Phase difference between the object and its image is zero.
The correct Answer is:B, C
1v−1(−3f)=1f
v=3f2
hih0=v(−3f)
hi=−h02
Amplitude =A2
Phase differnece is π.
Similar Questions
An object kept near a convex lens of focal length f, executes SHM between P and Q according to the equation y=Asinωt, O being the mean position. Take x-axis as the principal axis of the lens and A<<D to answer the following questions:
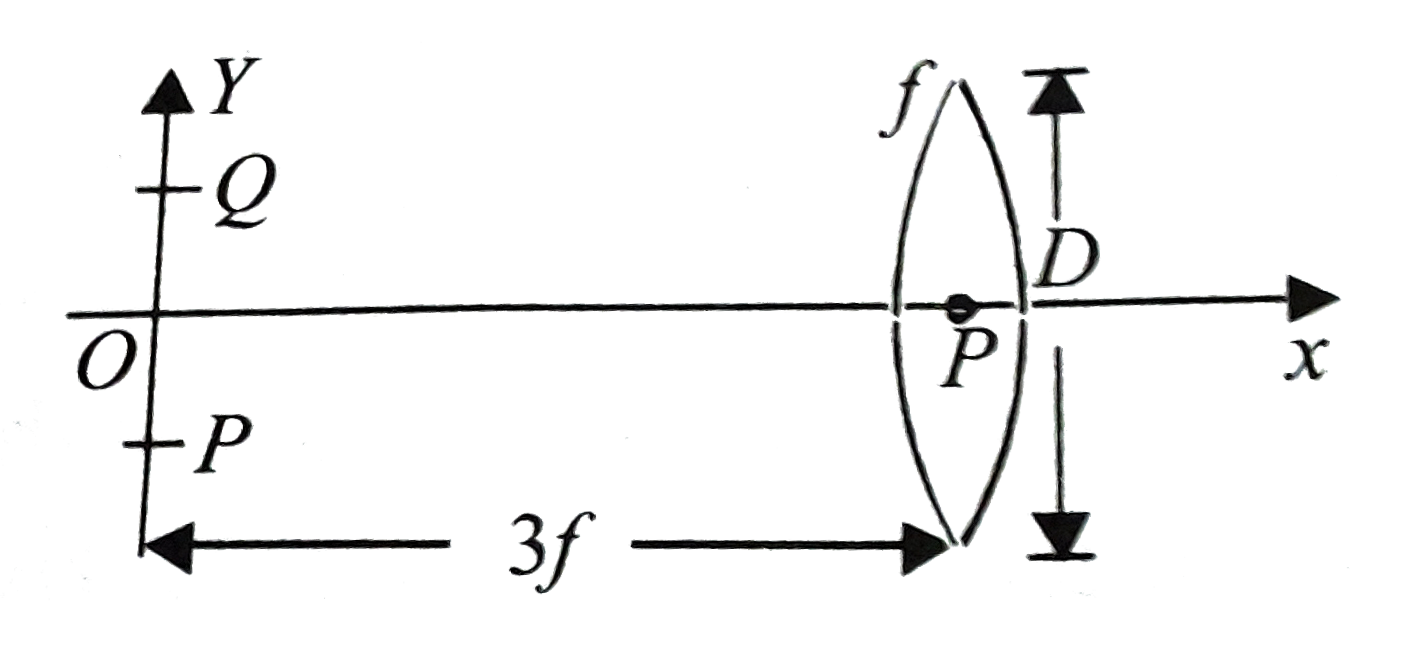
Q. The velocity of the image when the object crosses the mean position and goes toward Q isView SolutionAn object kept near a convex lens of focal length f, executes SHM between P and Q according to the equation y=Asinωt, O being the mean position. Take x-axis as the principal axis of the lens and A<<D to answer the following questions:
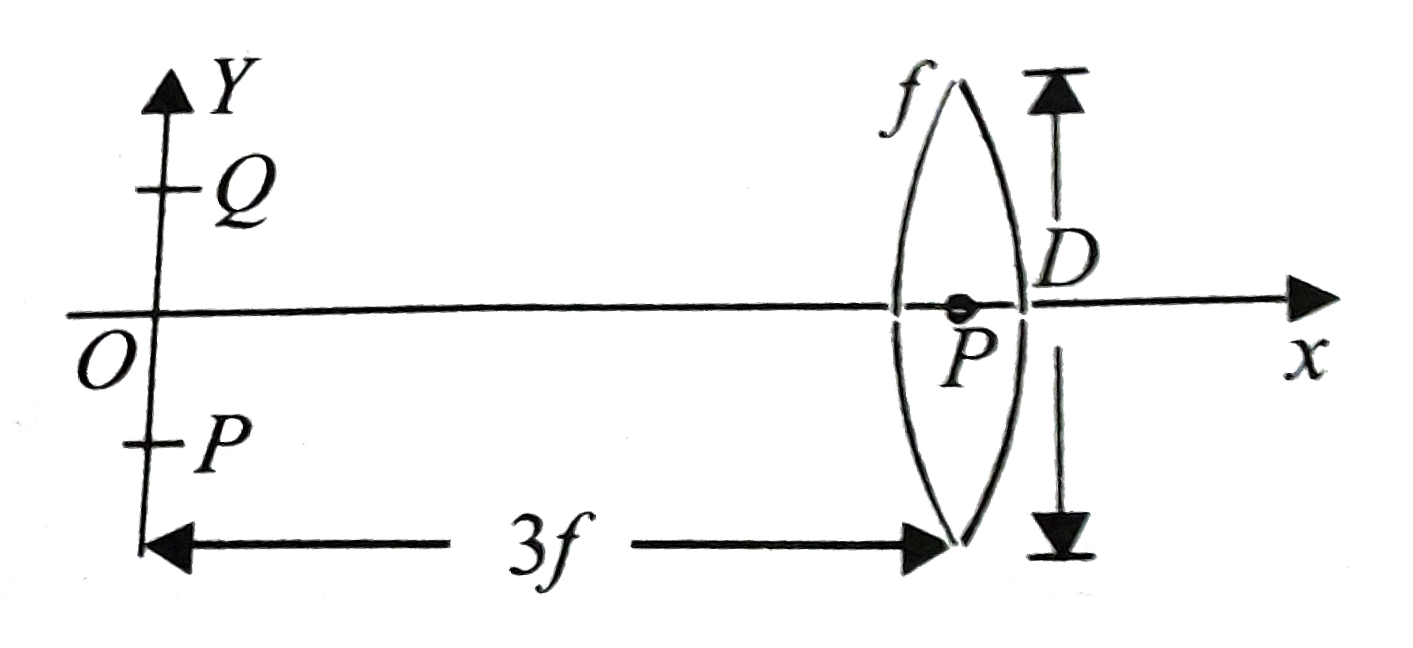
Q. The phase difference between the object and the image oscillations isView SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
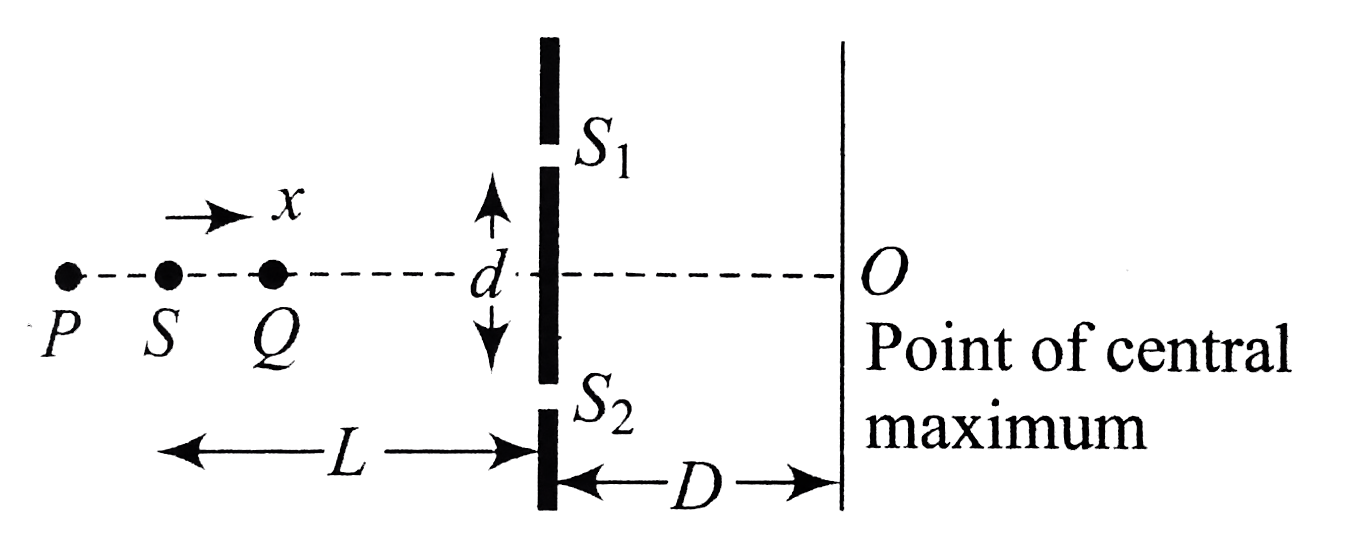
When the source comes toward the point Q,View SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
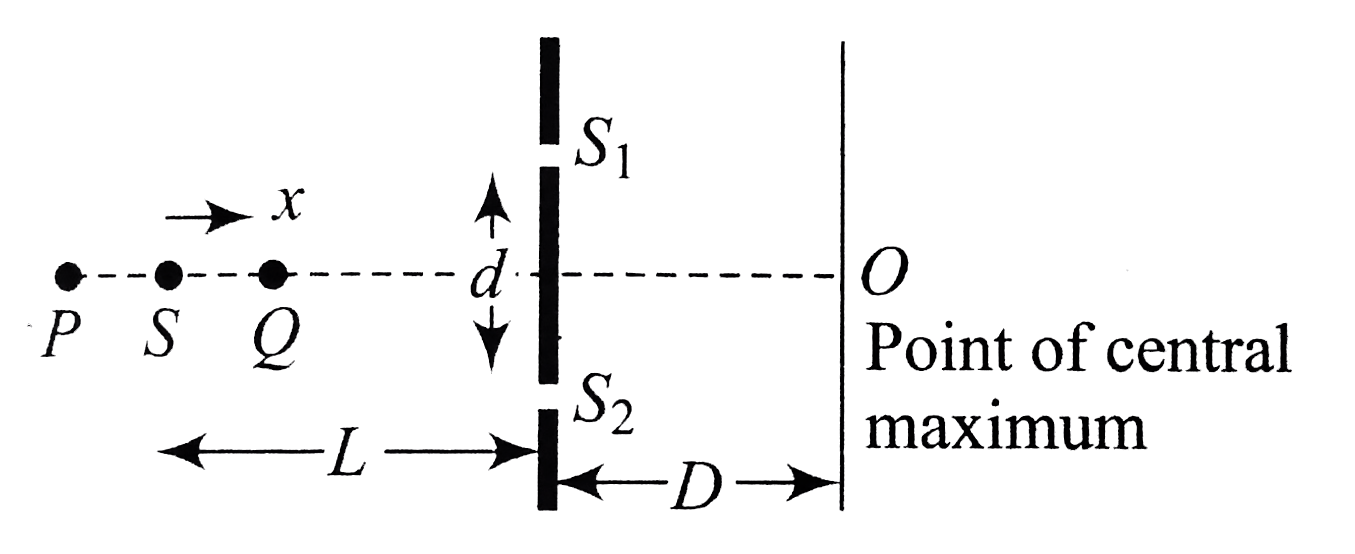
The fringe width β can be expressed asView SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
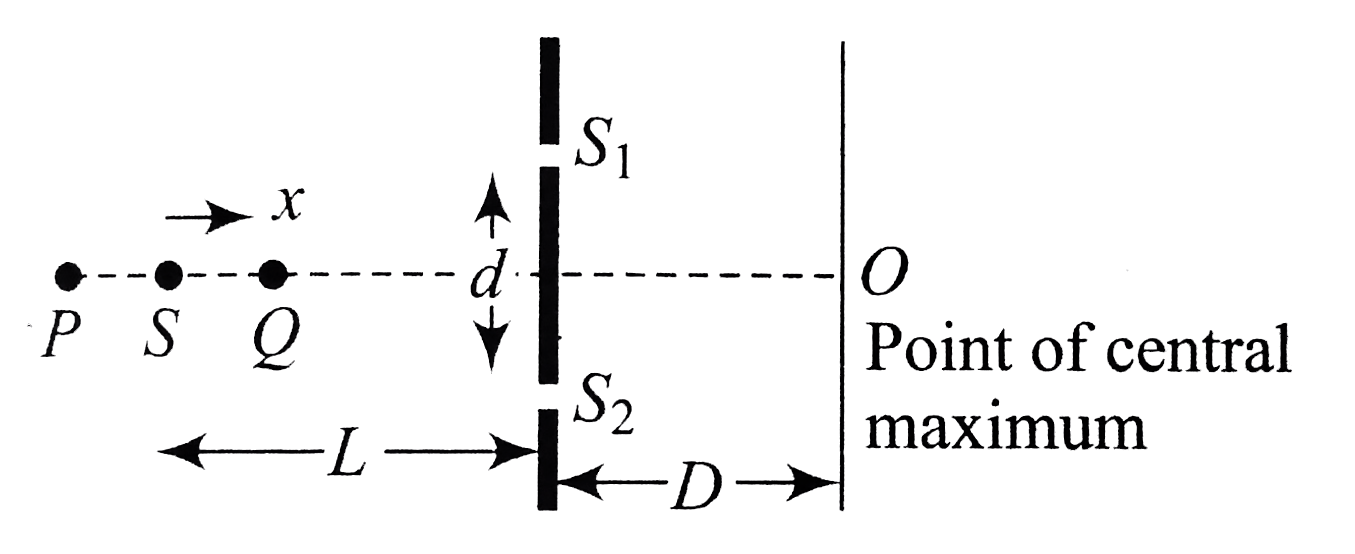
The fractional change in intensity of the central maximum as function of time isView SolutionA thin linear object of size 1mm is kept along the principal axis of a convex lens of focal length 10cm. The object is at 15cm from the lens. The length of the image is:
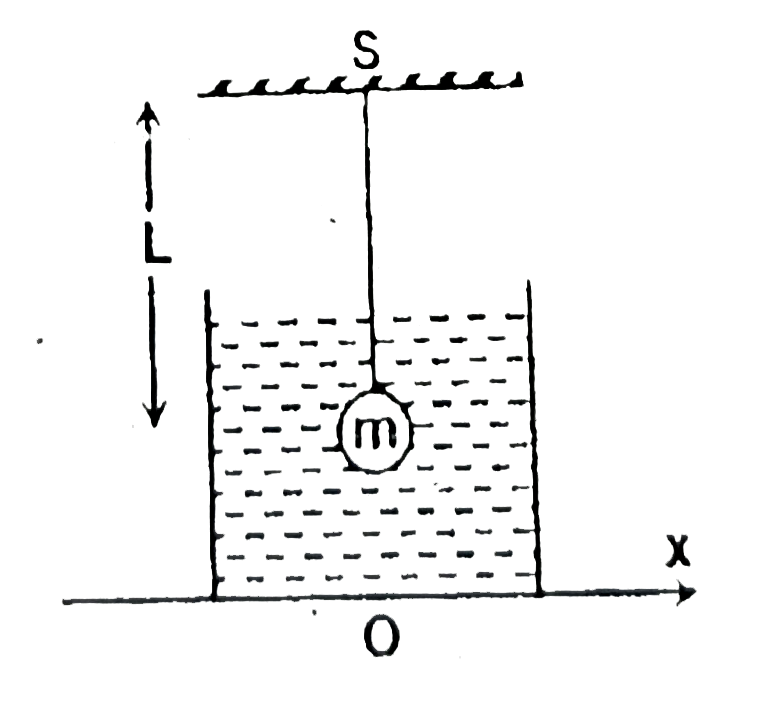
View SolutionA beaker containing an ideal fluid executes plane SHM in a horizontal plane according to the equation x=√3gω2sinωt, O being the mean position. A bob is suspended at S through a string of length L as shown in the figure. The line SO is vertical. Assuming L>>√3gω2.
The magnitude of maximum buoyant force and the time with it occurs for the second time are, respectively
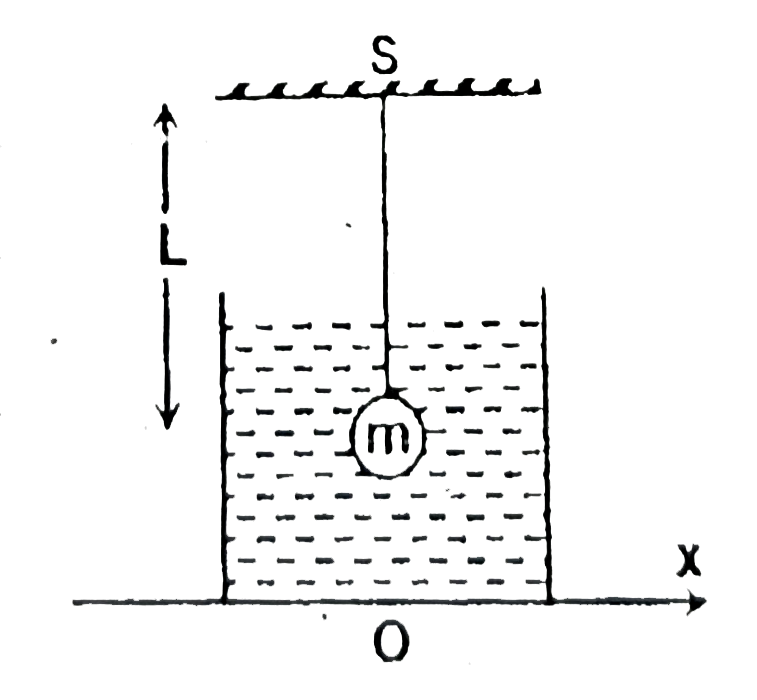 View Solution
View SolutionA beaker containing an ideal fluid executes plane SHM in a horizontal plane according to the equation x=√3gω2sinωt, O being the mean position. A bob is suspended at S through a string of length L as shown in the figure. The line SO is vertical. Assuming L>>√3gω2.
The direction of buoyant force at time t=π/2ω is best represented by
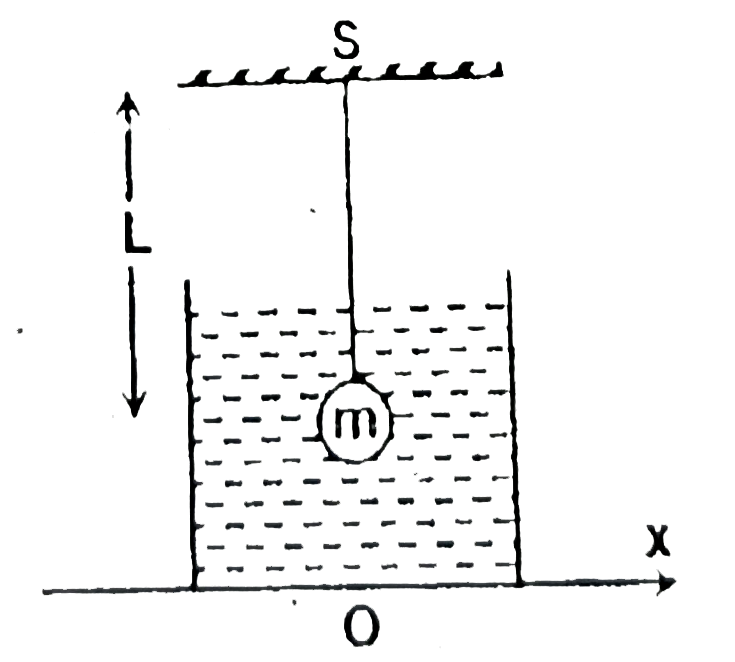 View Solution
View SolutionA beaker containing an ideal fluid executes plane SHM in a horizontal plane according to the equation x=√3gω2sinωt, O being the mean position. A bob is suspended at S through a string of length L as shown in the figure. The line SO is vertical. Assuming L>>√3gω2.
The tension in the string is maximum at time t=
 View Solution
View SolutionA convex lens of focal length f and a plane mirror are y distance apart. An object O is kept on the principal axis of the lens at a distance x from the lens. The values of x and y for the final image of O to fall exactly (position and size) on the object O are :
 View Solution
View Solution

