A beaker containing an ideal fluid executes plane SHM in a horizontal plane according to the equation x=√3gω2sinωt, O being the mean position. A bob is suspended at S through a string of length L as shown in the figure. The line SO is vertical. Assuming L>>√3gω2.
The magnitude of maximum buoyant force and the time with it occurs for the second time are, respectively
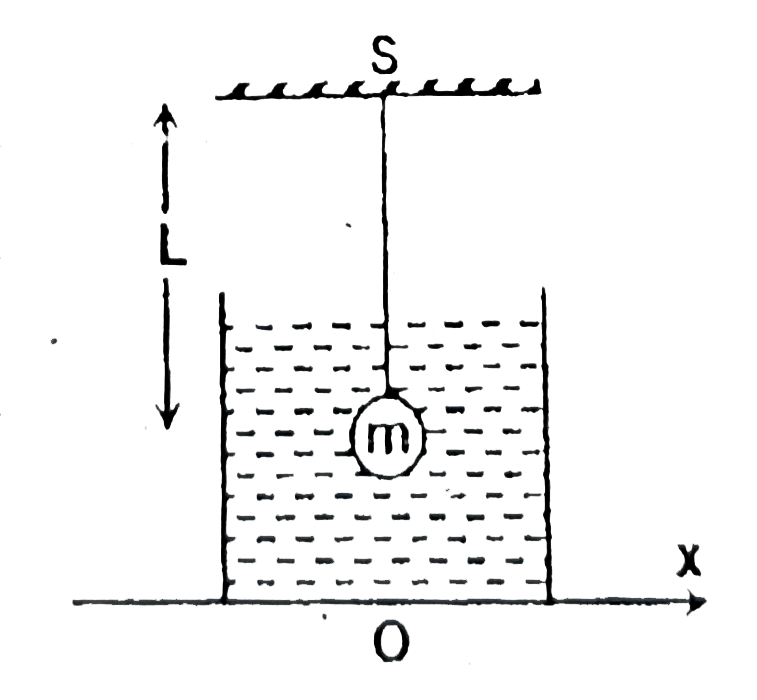
2g, π/2ω
g, 3π/ω
2g, 3π/2
g, π/ω
(C) 2ρVg, 3π/2ω
Magnitude of component of Buoyant force =ρva
Where a is acceleration of beaker, a=−√3gsinωt
Net buoyant force =√ρ2v2g2+ρ2v2a2
=ρvg√1+3sin2ωt
Magnitude of maximum buoyant force =2ρvg
sin2ωt=1 at t=π2ω, 3π2ω
∴2ρvg, 3π2ω
Similar Questions
A beaker containing an ideal fluid executes plane SHM in a horizontal plane according to the equation x=√3gω2sinωt, O being the mean position. A bob is suspended at S through a string of length L as shown in the figure. The line SO is vertical. Assuming L>>√3gω2.
The tension in the string is maximum at time t=
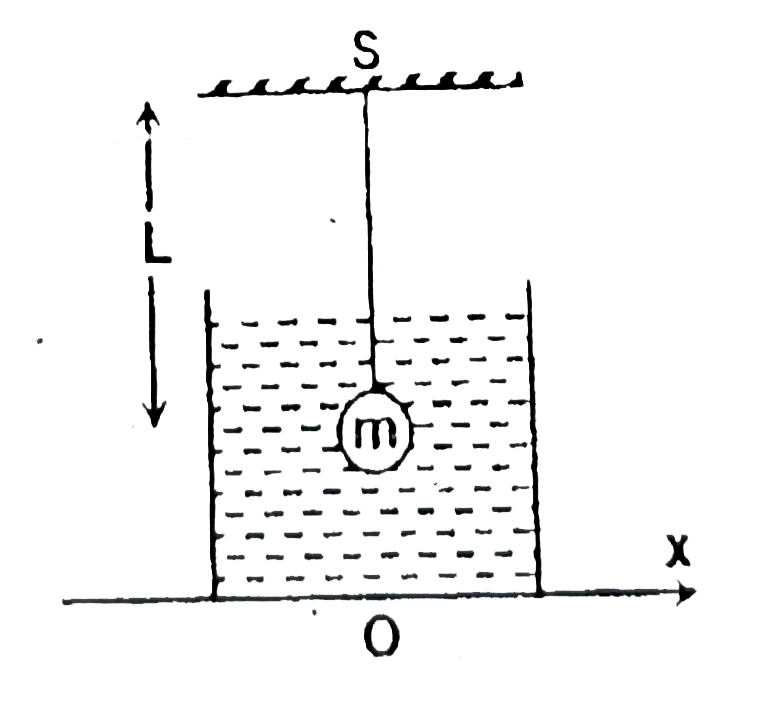
View SolutionA beaker containing an ideal fluid executes plane SHM in a horizontal plane according to the equation x=√3gω2sinωt, O being the mean position. A bob is suspended at S through a string of length L as shown in the figure. The line SO is vertical. Assuming L>>√3gω2.
The direction of buoyant force at time t=π/2ω is best represented by
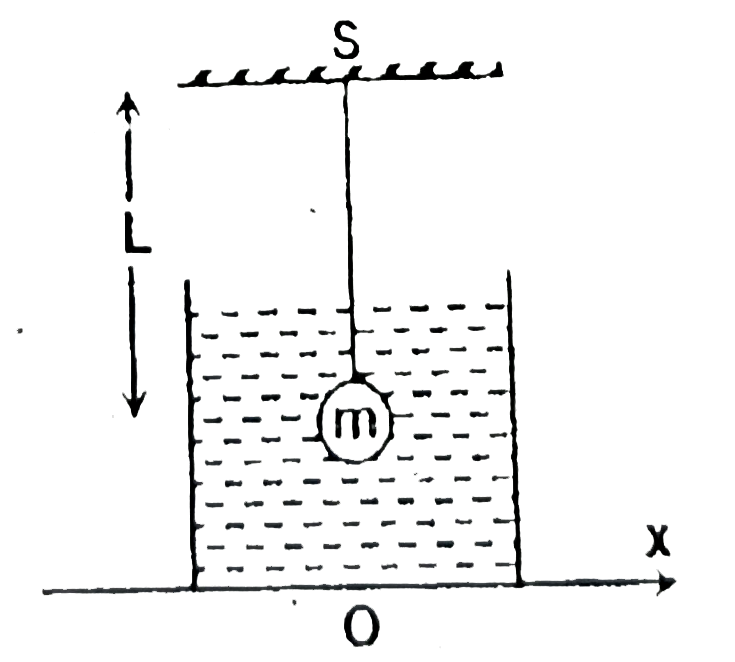
View SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
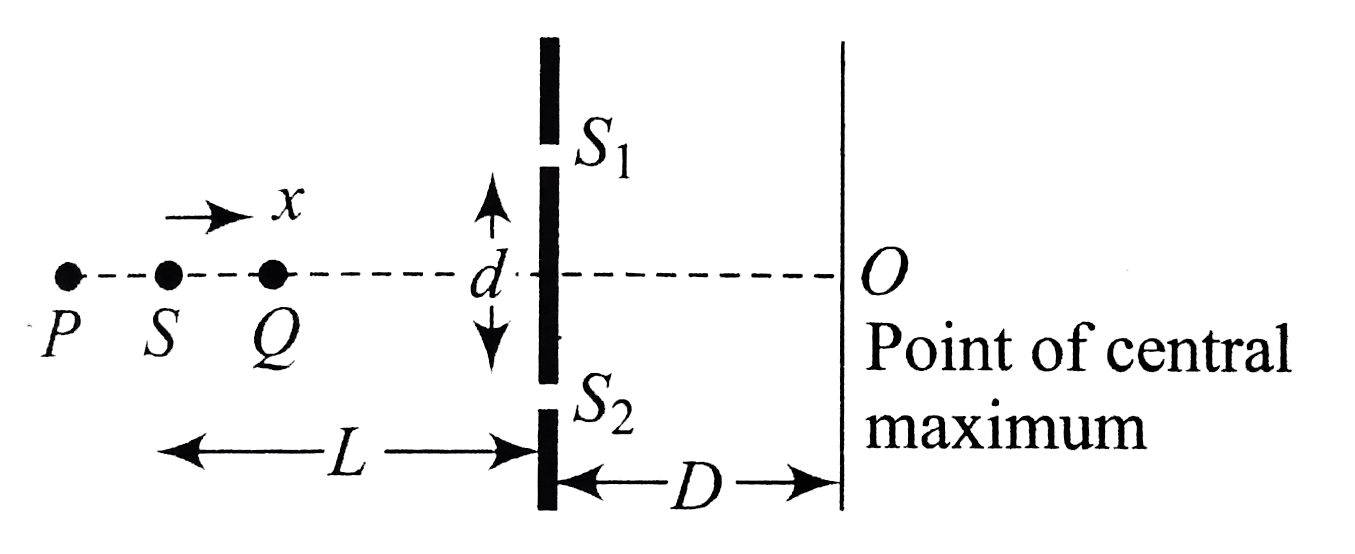
When the source comes toward the point Q,
View SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
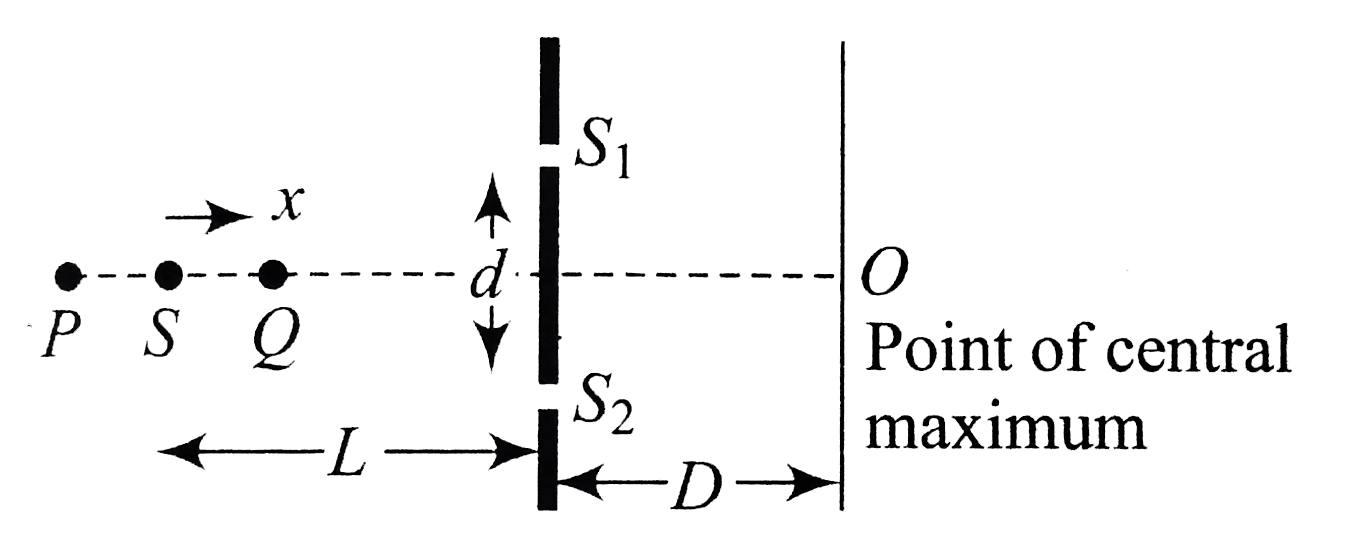
The fractional change in intensity of the central maximum as function of time is
View SolutionA block can slide along incline plane as shown in figure. The acceleration of chamber is 2√3gm/s2 horizontally as shown. Find the time when the block collide with the vertical wall AB of the chamber ( take g =10m/s2 )

View SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
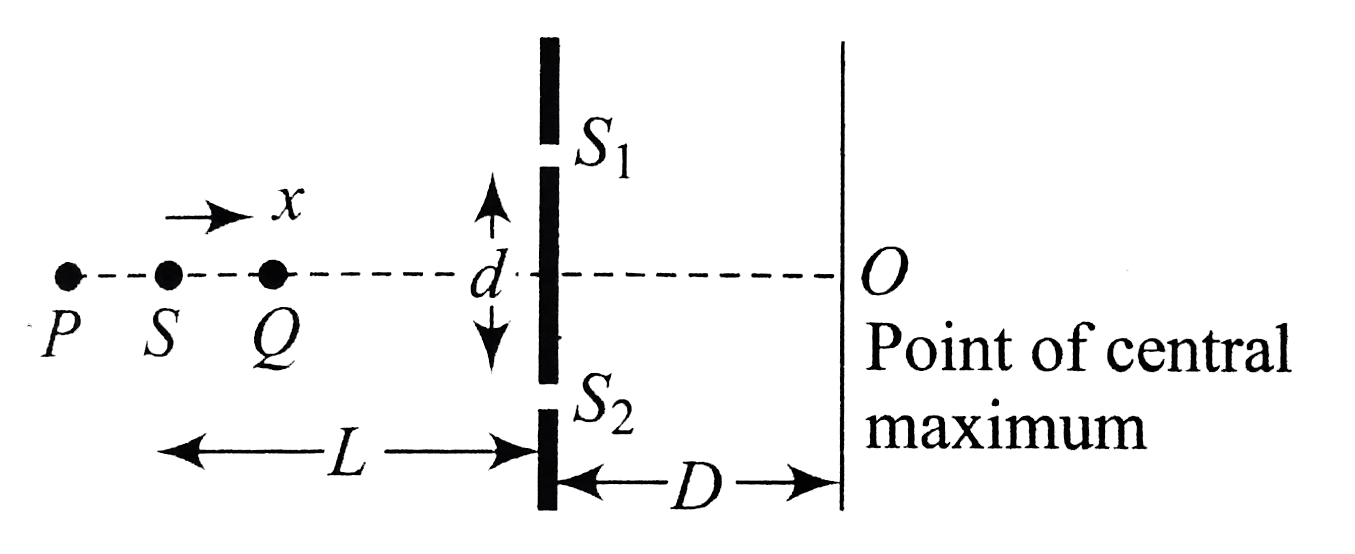
The fringe width β can be expressed as
View SolutionThree particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizontal frictionless table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity ω.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
View SolutionA car is moving with constant speed of 10m/s on a horizontal circular path of radius 10√3m . A bob of mass m suspended through a light string from the roof of the car. What is the angle made by the string with the vertical if the bob is stationary with respect to the car? (g = 10 m/s2)
View SolutionA bob of mass 2kg is suspended from point O of a core with an inextensible string strinng of length √3m. It is moving in horizontal circle over the surface of cone as shown in the figure. Then :(g=10m/s2)
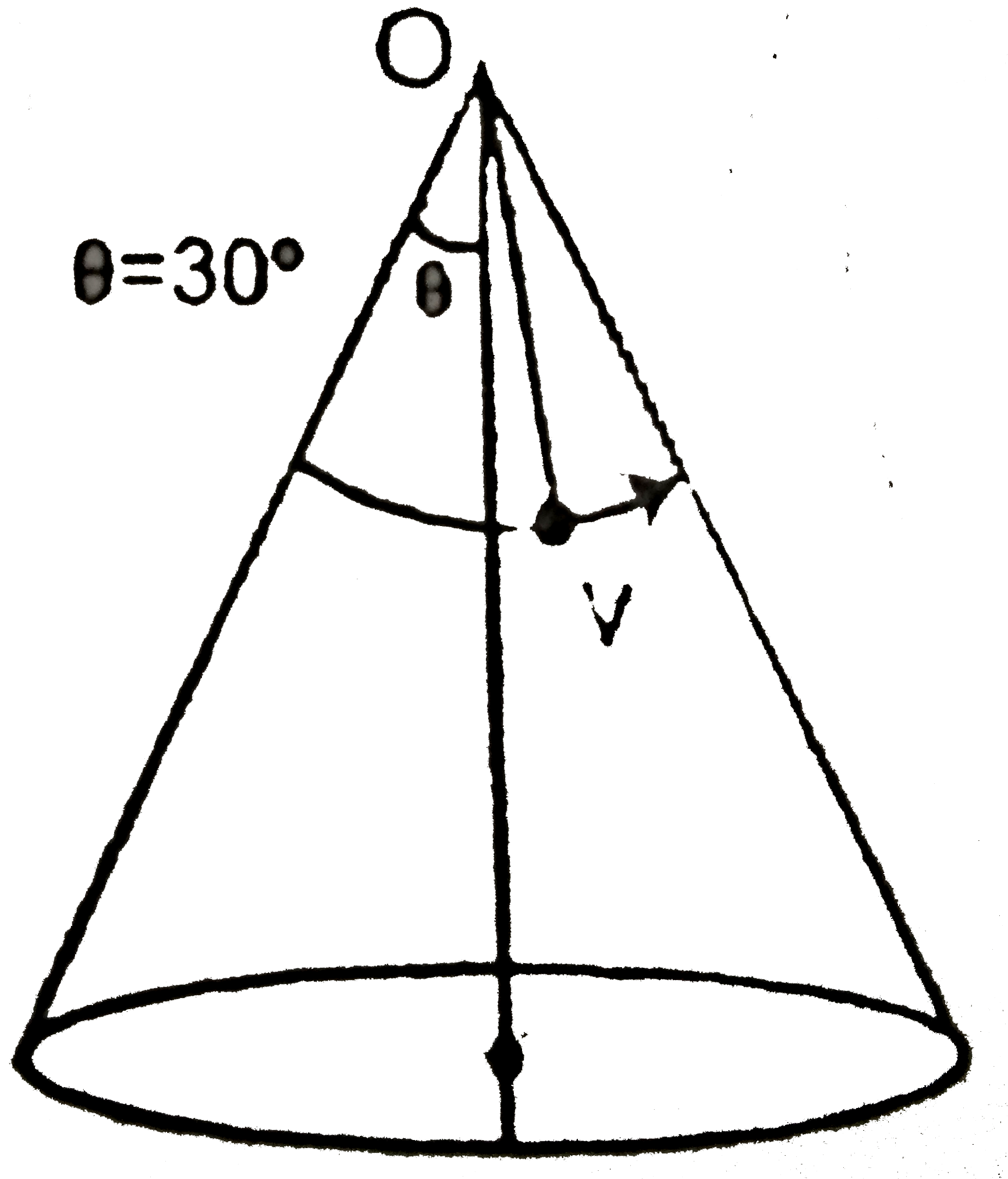
View SolutionA bob of mass 2kg is suspended from point O of a core with an inextensible string strinng of length √3m. It is moving in horizontal circle over the surface of cone as shown in the figure. Then :(g=10m/s2)

View Solution
