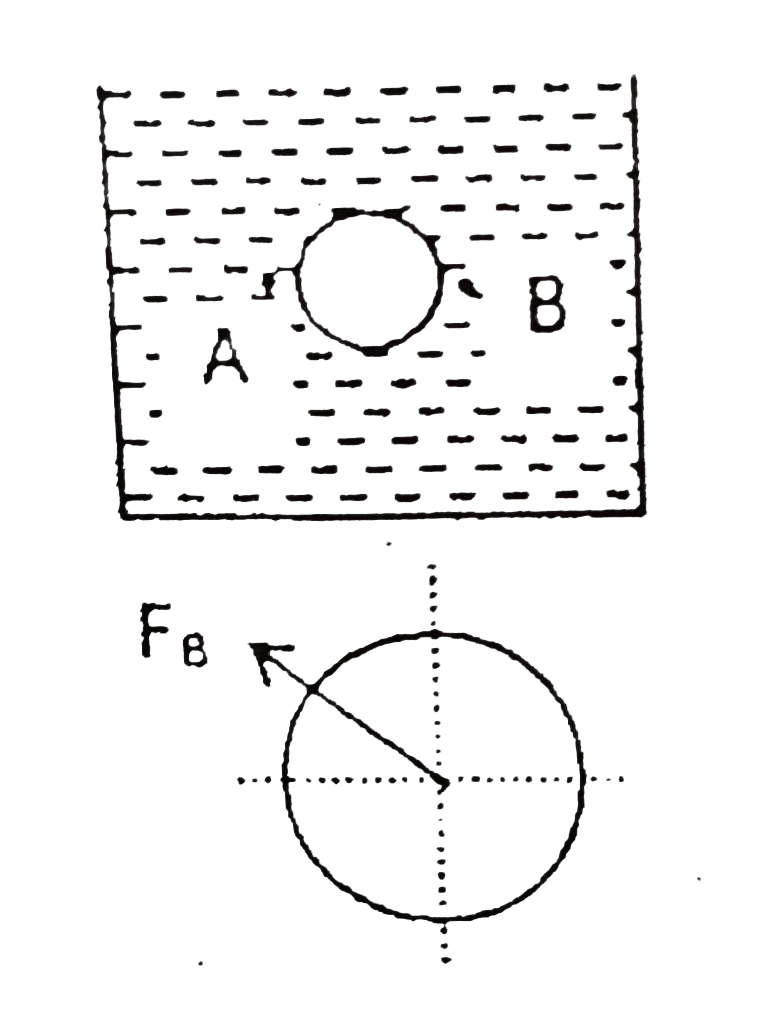
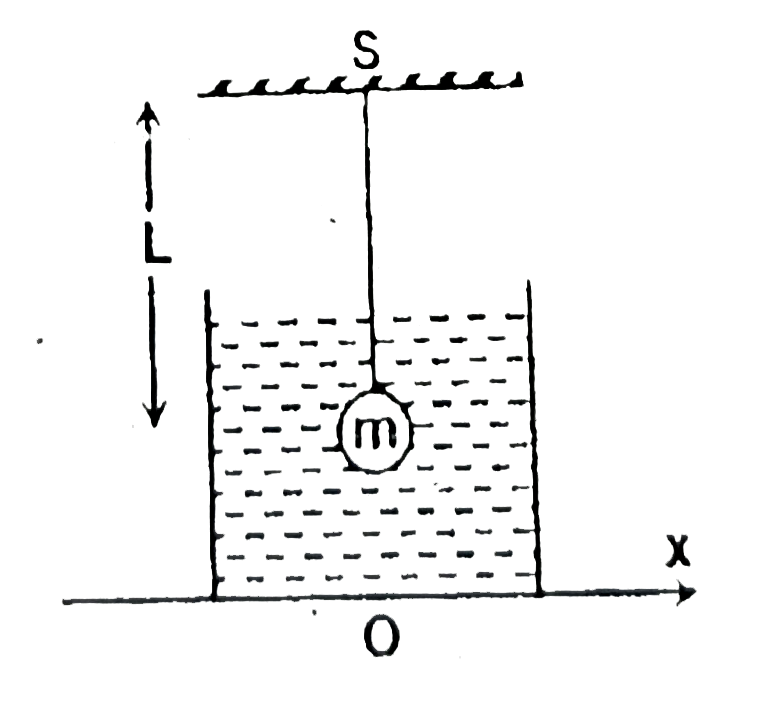
A beaker containing an ideal fluid executes plane SHM in a horizontal plane according to the equation x=√3gω2sinωt, O being the mean position. A bob is suspended at S through a string of length L as shown in the figure. The line SO is vertical. Assuming L>>√3gω2.
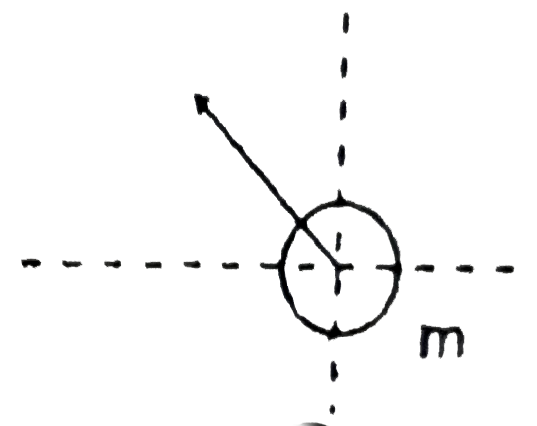
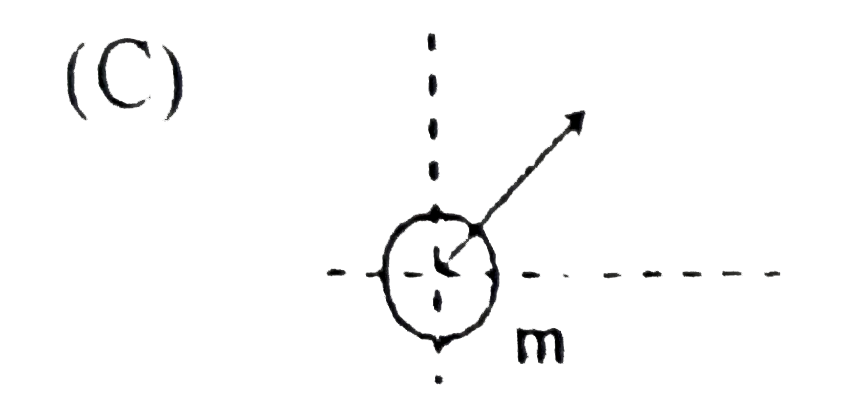
The direction of buoyant force at time t=π/2ω is best represented by

a=acceleration of beaker =−√3gsinωt
At t=π/2ω, a=−√3g
Pressure at B> Pressure at A
Horizontal comp. of Buoyant force acts towards left.
∴Direction of buoyant force.
Similar Questions
A beaker containing an ideal fluid executes plane SHM in a horizontal plane according to the equation x=√3gω2sinωt, O being the mean position. A bob is suspended at S through a string of length L as shown in the figure. The line SO is vertical. Assuming L>>√3gω2.
The tension in the string is maximum at time t=
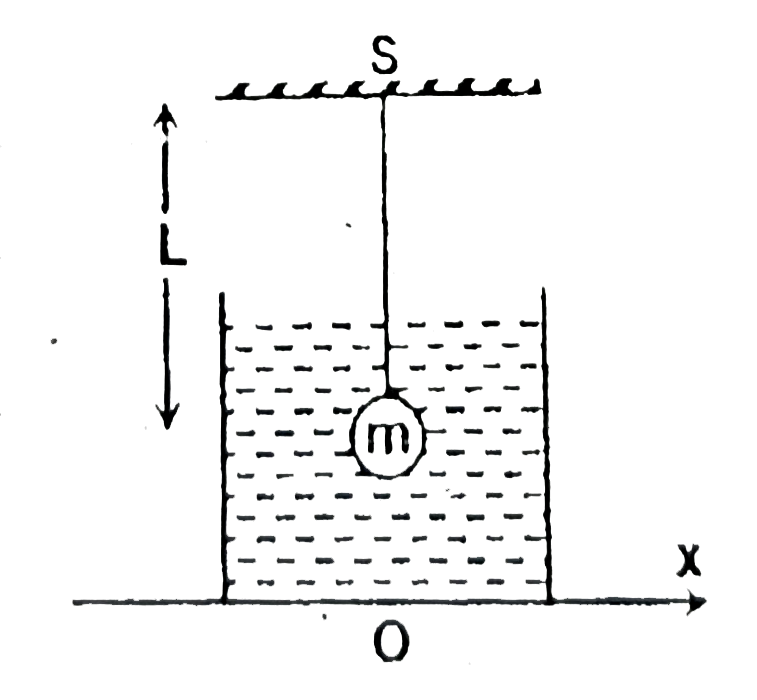
View SolutionA beaker containing an ideal fluid executes plane SHM in a horizontal plane according to the equation x=√3gω2sinωt, O being the mean position. A bob is suspended at S through a string of length L as shown in the figure. The line SO is vertical. Assuming L>>√3gω2.
The magnitude of maximum buoyant force and the time with it occurs for the second time are, respectively
View SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
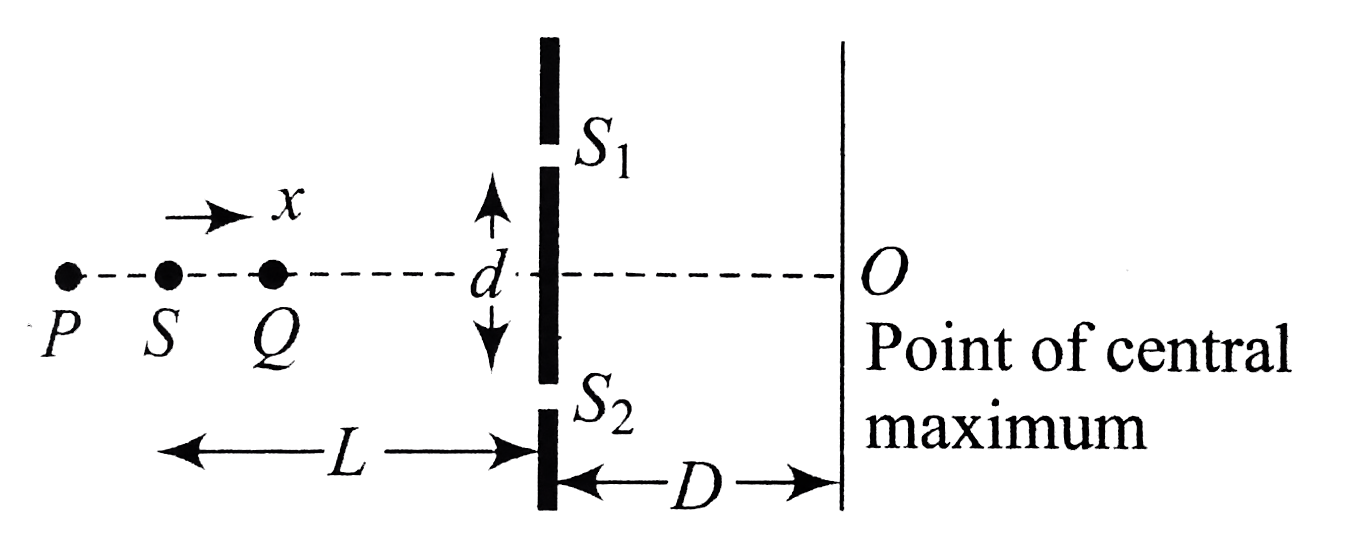
When the source comes toward the point Q,
View SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
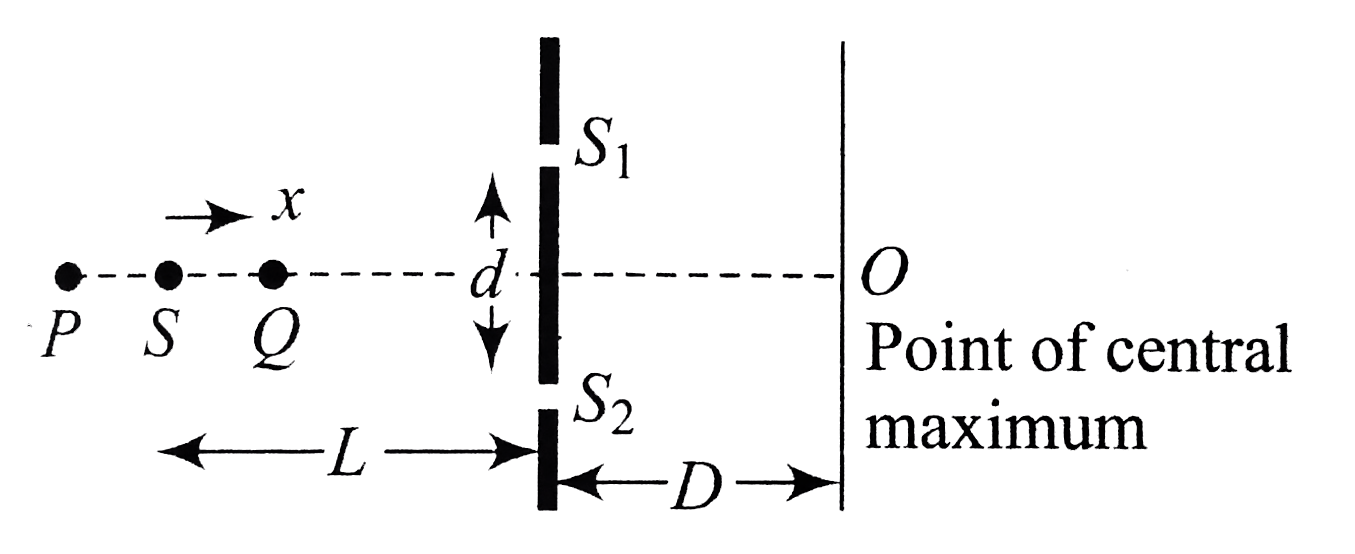
The fringe width β can be expressed as
View SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
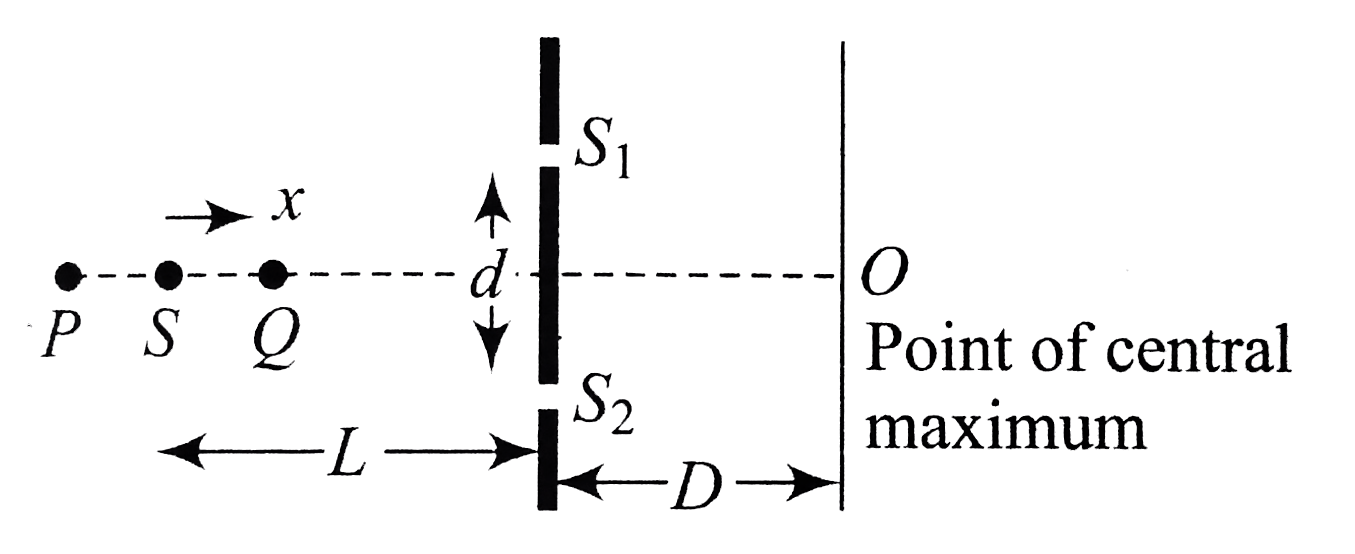
The fractional change in intensity of the central maximum as function of time is
View SolutionA car is moving with constant speed of 10m/s on a horizontal circular path of radius 10√3m . A bob of mass m suspended through a light string from the roof of the car. What is the angle made by the string with the vertical if the bob is stationary with respect to the car? (g = 10 m/s2)
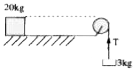
View SolutionA body of mass 20kg is moving on a rough horizontal plane. A block of mass 3kg is connected to the 20 kg mass by a string of negligible mass through a smooth pulley as shown in the figure. The tension in the string is 27 N. The coefficient of kinetic friction between the heavier mass and the surface is (g = 10m/s2)
View SolutionA bob of mass 2kg is suspended from point O of a core with an inextensible string strinng of length √3m. It is moving in horizontal circle over the surface of cone as shown in the figure. Then :(g=10m/s2)
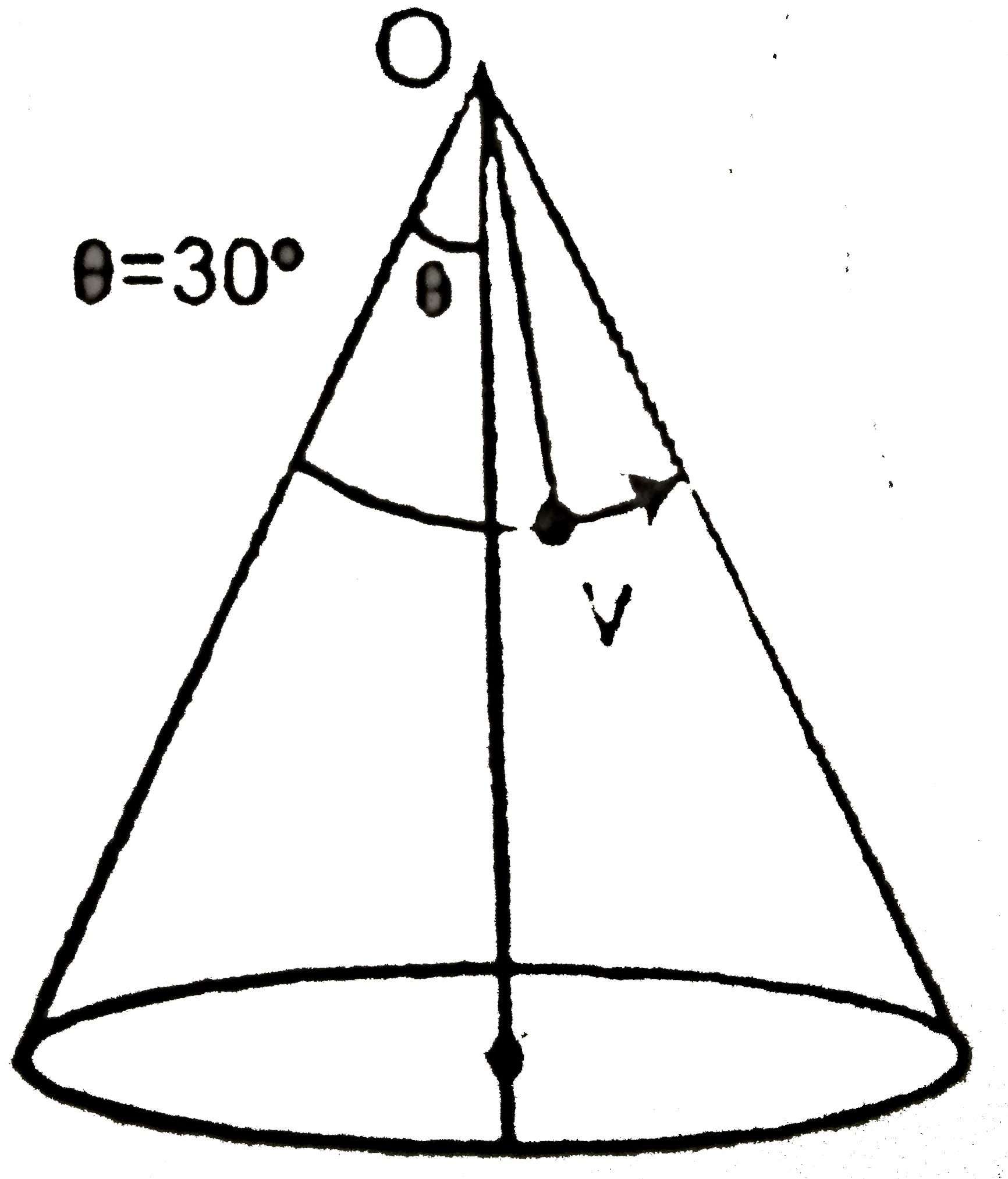
View SolutionA bob of mass 2kg is suspended from point O of a core with an inextensible string strinng of length √3m. It is moving in horizontal circle over the surface of cone as shown in the figure. Then :(g=10m/s2)

View SolutionA bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The horizontal coordinate of the intital position of the bob w.r.t. the point of firing of the bullet is n
View Solution
