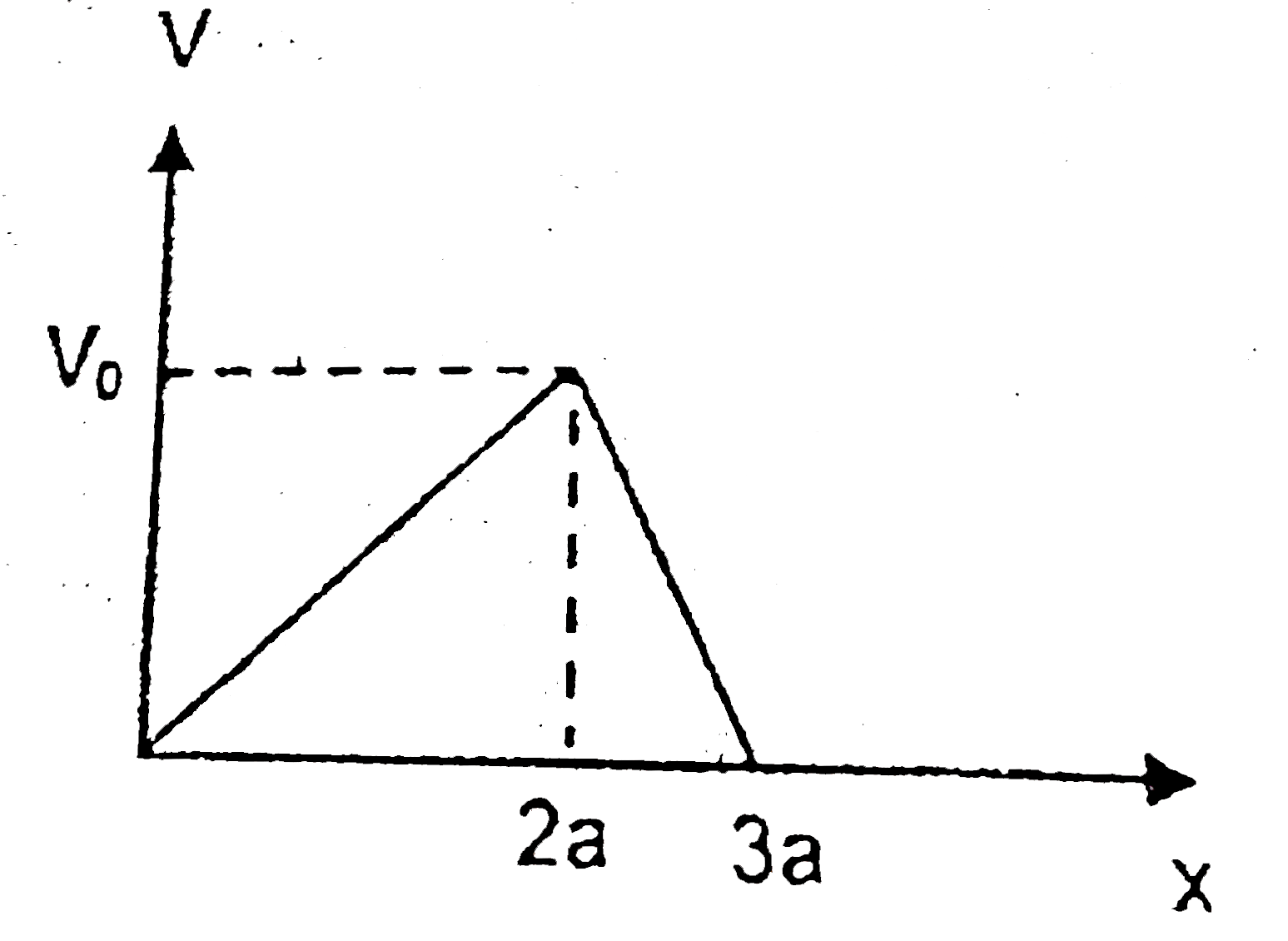
There exist electric field in space such that potential gradient along y-axis and z-axis is zero. Figure shows variation of potential with x coordinate. It implies that there should be
A.An infinite long line charge parallel to z-axis at with linear charge density
B.An infinite large sheet parallel to yz plane at with surface charge density
C.An infinite large sheet parallel to yz plane at withh surface charge density
D.An inifinite large sheet parallel to yz plane at with surface charge density
The correct Answer is:D
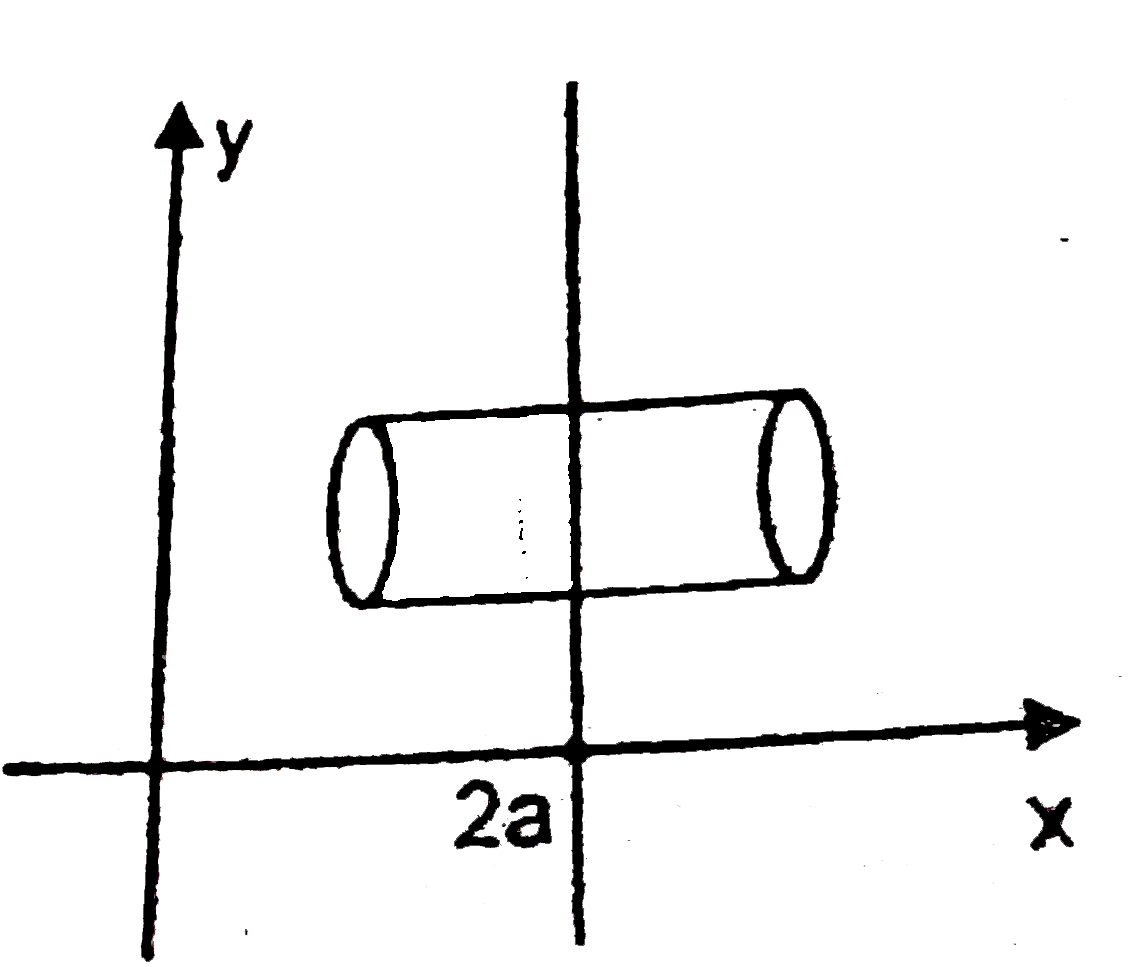
Gauss law for cylindrical
Similar Questions
Show that the electric field at any point is equal to negative potential gradient at the point.
View SolutionShow that the electric field at any point is equal to negative potential gradient at the point.
View SolutionAn electric field →E=20yˆj exist in space . The potential at (5 m, 5 m) is taken to be zero. The potential at origin is
View SolutionThe slope of the graph showing the variation of potential difference V on X-axis and current Y-axis gives conductor
View SolutionTwo identical positive charges are placed at x=−a and x=a. The correct variation of potential V along the x-axis is given by
View SolutionAn electric field E=(20ˆi+30ˆj) N/C exists in the space. If the potential at the origin is taken be zero, find the potential at (2m,2m).
View Solution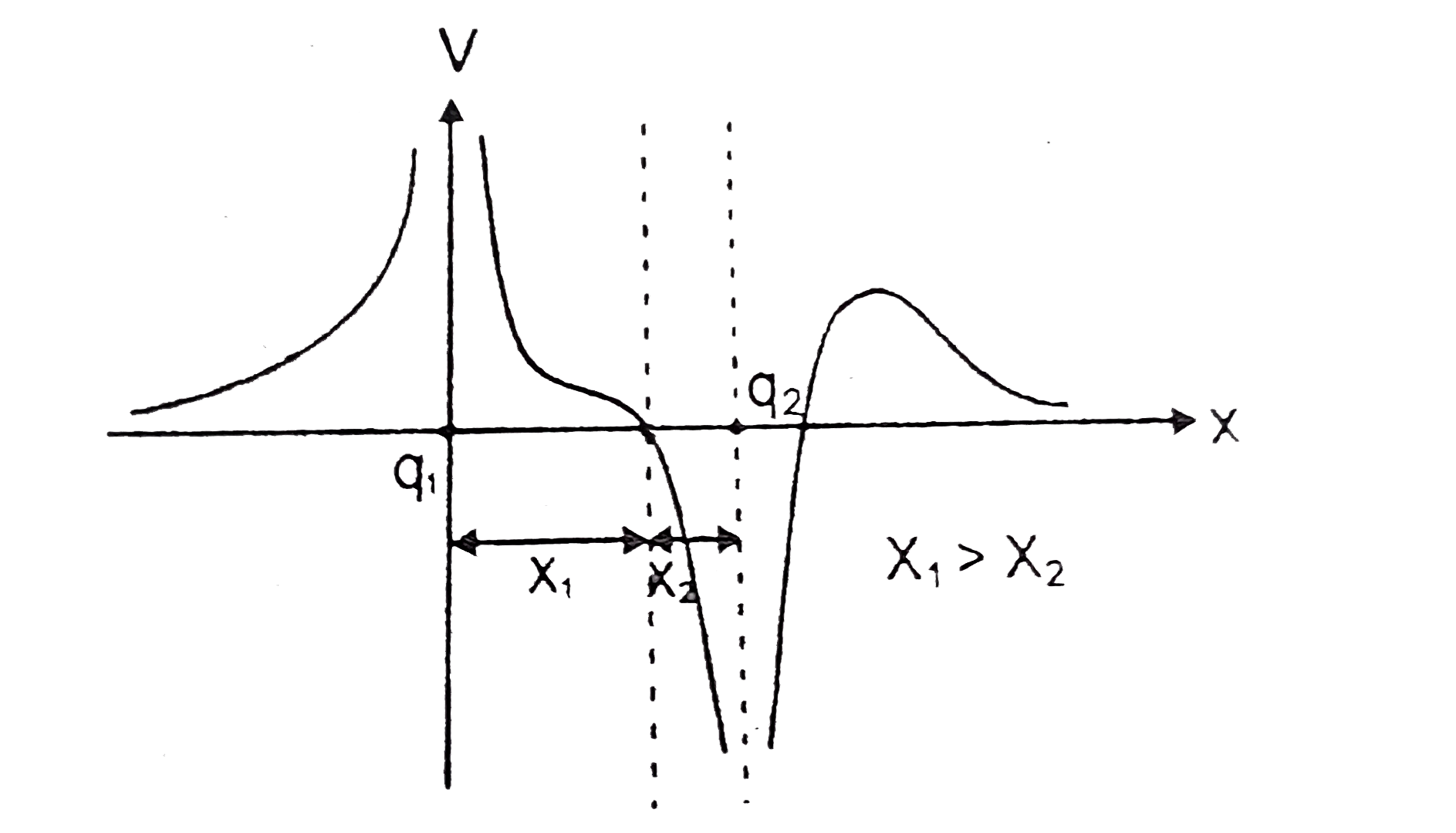
Two point charges (q1 and q2) are placed on x-axis, figure shows graph potential (V) on x-axis. With x-co-ordinate:
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential difference VA−VO, where VO is the potential at the origin and VA the potential at x=2m is:
View SolutionA dipole is placed in xy plane parallel to the line y=2x. There exists a uniform electric field along z-axis. Net force acting on the dipole will be zero. But it can experience some torque. We can show that the direction of this torque will be parallel to the line.
View Solution
