P is the centre of mass of four point masses A,B, C and D which are lying in the same length but not along the same straight line then.
a. P must lie with in the quadrilateral ABCD.
b. P may or may not coincide with one of the point masses.
c. P must lie on a line joining two of the points A, B, C, D.
d. P may lie outside the quadrilateral ABCD.
The correct Answer is:B, D
To determine the position of the center of mass (P) of four point masses (A, B, C, and D) that are lying in the same plane but not along the same straight line, we can analyze the situation step by step.
1. Understanding the Configuration:
- We have four point masses A, B, C, and D positioned in a two-dimensional plane. They are not aligned in a straight line, meaning they form a quadrilateral shape.
2. Defining the Center of Mass:
- The center of mass (P) of a system of particles is defined as the point where the total mass of the system can be considered to be concentrated. For point masses, the center of mass can be calculated using the formula:
→Rcm=1Mn∑i=1mi→ri
where M is the total mass, mi are the individual masses, and →ri are their position vectors.
3. Analyzing the Position of P:
- Since the masses are arranged in a quadrilateral, we can visualize that the center of mass P will lie within the area enclosed by the quadrilateral formed by the points A, B, C, and D. This is based on the principle that the center of mass of a system of particles lies within the convex hull formed by those particles.
4. Evaluating the Options:
- Option A: P must lie within the quadrilateral ABCD. This statement is true because the center of mass for a system of particles will always lie within the convex shape formed by those particles.
- Option B: P may or may not coincide with one of the point masses. This is also true because depending on the arrangement and the masses, the center of mass can coincide with one of the masses or be located elsewhere.
- Option C: P must lie on the line joining two of the point masses A, B, C, D. This statement is false because the center of mass does not have to lie on the line connecting any two masses; it can be located anywhere within the quadrilateral.
- Option D: P may lie outside the quadrilateral ABCD. This is false as the center of mass will always lie within the convex hull formed by the masses.
5. Conclusion:
- Based on the analysis, the correct option is A: P must lie within the quadrilateral ABCD.
- We have four point masses A, B, C, and D positioned in a two-dimensional plane. They are not aligned in a straight line, meaning they form a quadrilateral shape.
- The center of mass (P) of a system of particles is defined as the point where the total mass of the system can be considered to be concentrated. For point masses, the center of mass can be calculated using the formula:
→Rcm=1Mn∑i=1mi→ri
where M is the total mass, mi are the individual masses, and →ri are their position vectors.
- Since the masses are arranged in a quadrilateral, we can visualize that the center of mass P will lie within the area enclosed by the quadrilateral formed by the points A, B, C, and D. This is based on the principle that the center of mass of a system of particles lies within the convex hull formed by those particles.
- Option A: P must lie within the quadrilateral ABCD. This statement is true because the center of mass for a system of particles will always lie within the convex shape formed by those particles.
- Option B: P may or may not coincide with one of the point masses. This is also true because depending on the arrangement and the masses, the center of mass can coincide with one of the masses or be located elsewhere.
- Option C: P must lie on the line joining two of the point masses A, B, C, D. This statement is false because the center of mass does not have to lie on the line connecting any two masses; it can be located anywhere within the quadrilateral.
- Option D: P may lie outside the quadrilateral ABCD. This is false as the center of mass will always lie within the convex hull formed by the masses.
- Based on the analysis, the correct option is A: P must lie within the quadrilateral ABCD.
Similar Questions
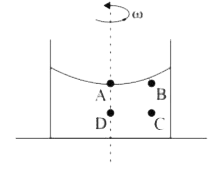
A cylindrical container filled with a liquid is being rotated about its central axis at a constant angular velocity ω. Four points A, B, C and D are chosen in the same plane such that ABCD is a square of side length a and AB is horizontal while BC is vertical. A and D lie on the axis of rotation. Let the pressure at A, B, C and D be denoted by PA,PB,PC and PD. Which of these options is correct ?
View SolutionThere are 15 points in a plane, no three of which are in the same straight line with the exception of 6, which are all in the same straight line. Find the number of i. straight lines formed, ii. number of triangles formed by joining these points.
View SolutionThere are ten points in a plane. Of these ten points, four points are in a straight line and with the exceptionof these four points, on three points are in the same straight line. Find i. the number of triangles formed, ii the number of straight lines formed iii the number of quadrilaterals formed, by joining these ten points.
View SolutionFind the potential energy of the gravitational interation of a point mass of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line such that the point mass is at a distance 'a' from one end. Also find the force of their interaction.
View SolutionThe centre of mass of a solid cone along the line form the center of the base to the vertex is at
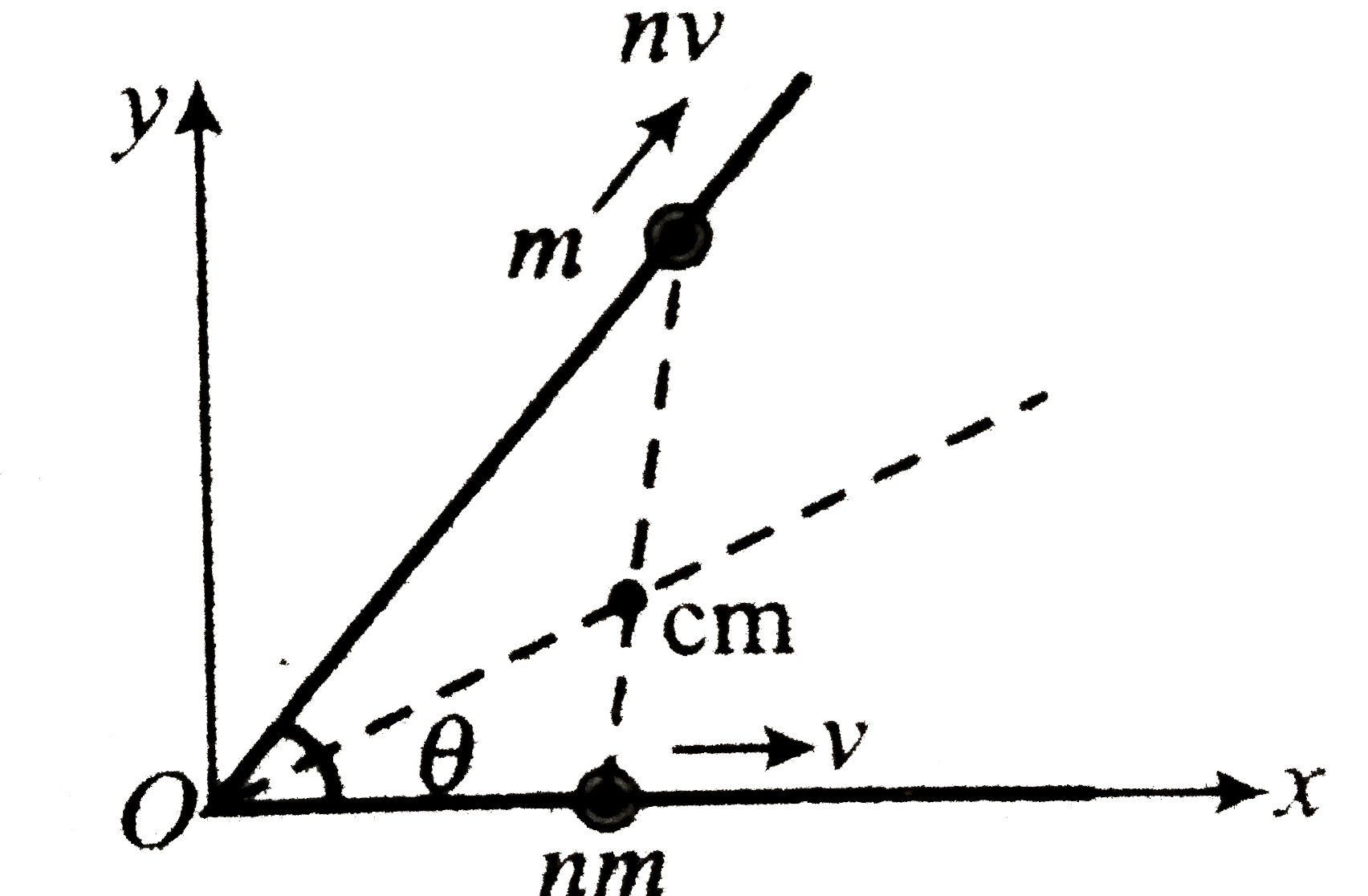
View SolutionTwo masses nm and m, start simultaneously from the intersection of two straight lines with velocities v and nv respectively. It is observed that the path of their centre of mass is a straight line bisecting the angle between the given straight lines. Find the magnitude of the velocity of centre of mass. [Here θ=angle between the lines]
View SolutionIf the angles of elevation of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
(a)ab
(b) √ab
(c) ab
(d) √ab
View SolutionTake four distinct point A,B ,C and D , out of which three points are collinear
Name the line segments.
View SolutionWhich of the following have same mass ?
View SolutionA point O is taken inside an equilateral four sided figure ABCD such that its distances from the angular points D and B are equal. Show that AO and OC are in one and the same straight line. GIVEN : A point O inside an equilateral quadrilateral four sided figure ABCD such that BO=OD. TO PROVE : AO and OC are in one and the same straight line.
View Solution
