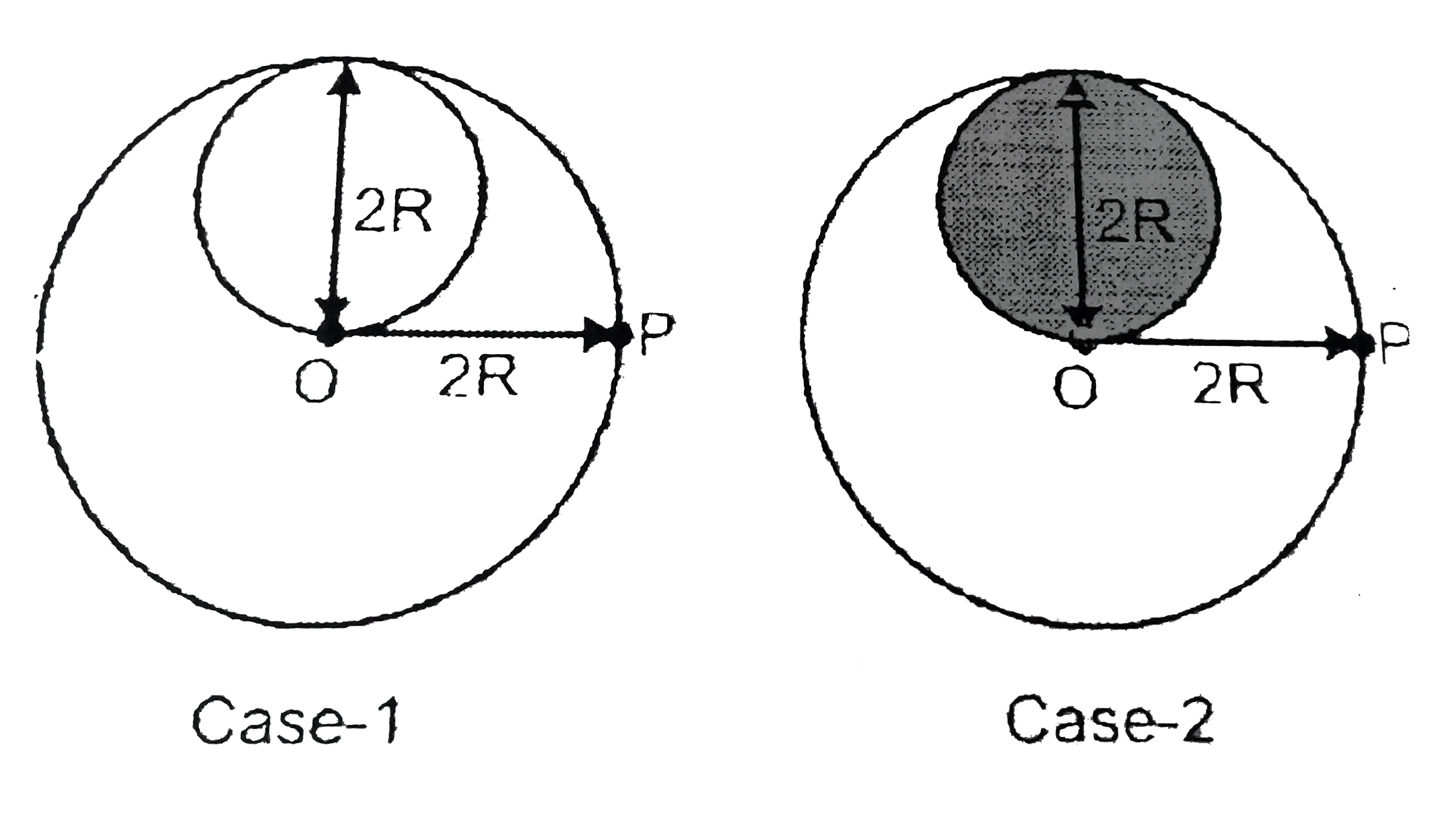
A lamina is made by removing a small disc of diameter 2 R from a bigger disc of uniform mass density and radius 2R, as shown in figure. A second similar disc is made but instead of hole a disc of triple the density as of first it filled in the hole. Centre of mass is calculated in both the cases and was found at a distance $r_{1} & r_{2}$ from centre $O$ respectively find the ratio $∣ ∣ ∣ \frac{2 r_{2}}{r_{1}} ∣ ∣ ∣$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

$r_{1} = \frac{[- σ \times π R^{2}] \times R}{[- σ \times π R^{2}] + [σ \times π {(2 R)}^{2}]}$
$& r_{2} = \frac{[2 σ \times π R^{2}] \times R}{[2 σ \times π R^{2}] + [σ \times π {(2 R)}^{2}]} \Rightarrow ∣ ∣ ∣ \frac{2 r_{2}}{r_{1}} ∣ ∣ ∣ = 2$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is $I_{O} and I_{P}$ respectively. Both these axes are perpendicular to the plane of the lamina. The ratio $\frac{I_{P}}{I_{O}}$ is

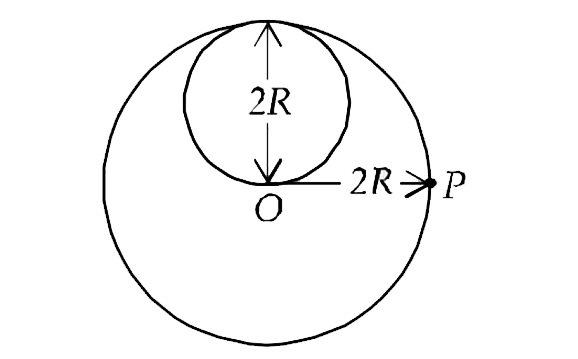A $13 / 37$
B $37 / 13$
C $73 / 31$
D $8 / 13$

Recommended Questions

Home
Ask Doubt
Profile