A parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
P.d. between the plates increases by 95%
P.d. between the plates decreases by 50%
P.d. between the plates increases by 50%
P.d. between the plates decreases by 95%
The correct Answer is:D
To solve the problem step by step, we will analyze the situation of a parallel plate capacitor when the separation between the plates is decreased and a dielectric slab is introduced.
Step 1: Understand the initial conditions
The initial capacitance C of the capacitor is given by the formula:
C=Kϵ0AD
where:
- K is the dielectric constant (initially K=1 since there is no dielectric),
- ϵ0 is the permittivity of free space,
- A is the area of the plates,
- D is the separation between the plates.
Step 2: Determine the charge on the capacitor
When the capacitor is charged to a potential V, the charge Q on the capacitor can be expressed as:
Q=C⋅V
Since the capacitor is disconnected from the battery, the charge Q remains constant.
Step 3: Analyze the new conditions after decreasing the plate separation
When the separation between the plates is decreased by 50%, the new separation D′ is:
D′=D2
Step 4: Introduce the dielectric slab
Now, we fill the space between the plates with a dielectric slab of dielectric constant K=10. The new capacitance C′ can be calculated as:
C′=Kϵ0AD′
Substituting D′:
C′=10ϵ0AD2=20ϵ0AD
Step 5: Relate the new capacitance to the initial capacitance
Since the initial capacitance C was:
C=ϵ0AD
We can express the new capacitance C′ in terms of C:
C′=20C
Step 6: Calculate the new potential difference
Since the charge Q remains constant, we can relate the new potential difference V′ to the new capacitance:
Q=C′⋅V′⟹V′=QC′
Substituting Q=C⋅V and C′=20C:
V′=C⋅V20C=V20
Step 7: Calculate the percentage decrease in potential
The percentage decrease in potential can be calculated as:
Percentage Decrease=V−V′V×100
Substituting V′=V20:
Percentage Decrease=V−V20V×100=20V−V20V×100=19V20V×100=95%
Conclusion
Thus, the potential difference between the plates decreases by 95%.
The initial capacitance C of the capacitor is given by the formula:
C=Kϵ0AD
where:
- K is the dielectric constant (initially K=1 since there is no dielectric),
- ϵ0 is the permittivity of free space,
- A is the area of the plates,
- D is the separation between the plates.
When the capacitor is charged to a potential V, the charge Q on the capacitor can be expressed as:
Q=C⋅V
Since the capacitor is disconnected from the battery, the charge Q remains constant.
When the separation between the plates is decreased by 50%, the new separation D′ is:
D′=D2
Now, we fill the space between the plates with a dielectric slab of dielectric constant K=10. The new capacitance C′ can be calculated as:
C′=Kϵ0AD′
Substituting D′:
C′=10ϵ0AD2=20ϵ0AD
Since the initial capacitance C was:
C=ϵ0AD
We can express the new capacitance C′ in terms of C:
C′=20C
Since the charge Q remains constant, we can relate the new potential difference V′ to the new capacitance:
Q=C′⋅V′⟹V′=QC′
Substituting Q=C⋅V and C′=20C:
V′=C⋅V20C=V20
The percentage decrease in potential can be calculated as:
Percentage Decrease=V−V′V×100
Substituting V′=V20:
Percentage Decrease=V−V20V×100=20V−V20V×100=19V20V×100=95%
Thus, the potential difference between the plates decreases by 95%.
Similar Questions
Two parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionA parallel plate capacitar, of capacitance, 20μF, is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
View Solution
Knowledge Check
A parallel plate capacitor with air between the plates has a capacitance of 10 pF. The capacitance, if the distance bgetween the plates is reduced by half and the space between tehm is filled with a substance of dielectric constant 4 is
A80pFB96pFC100pFD120pF
Answer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
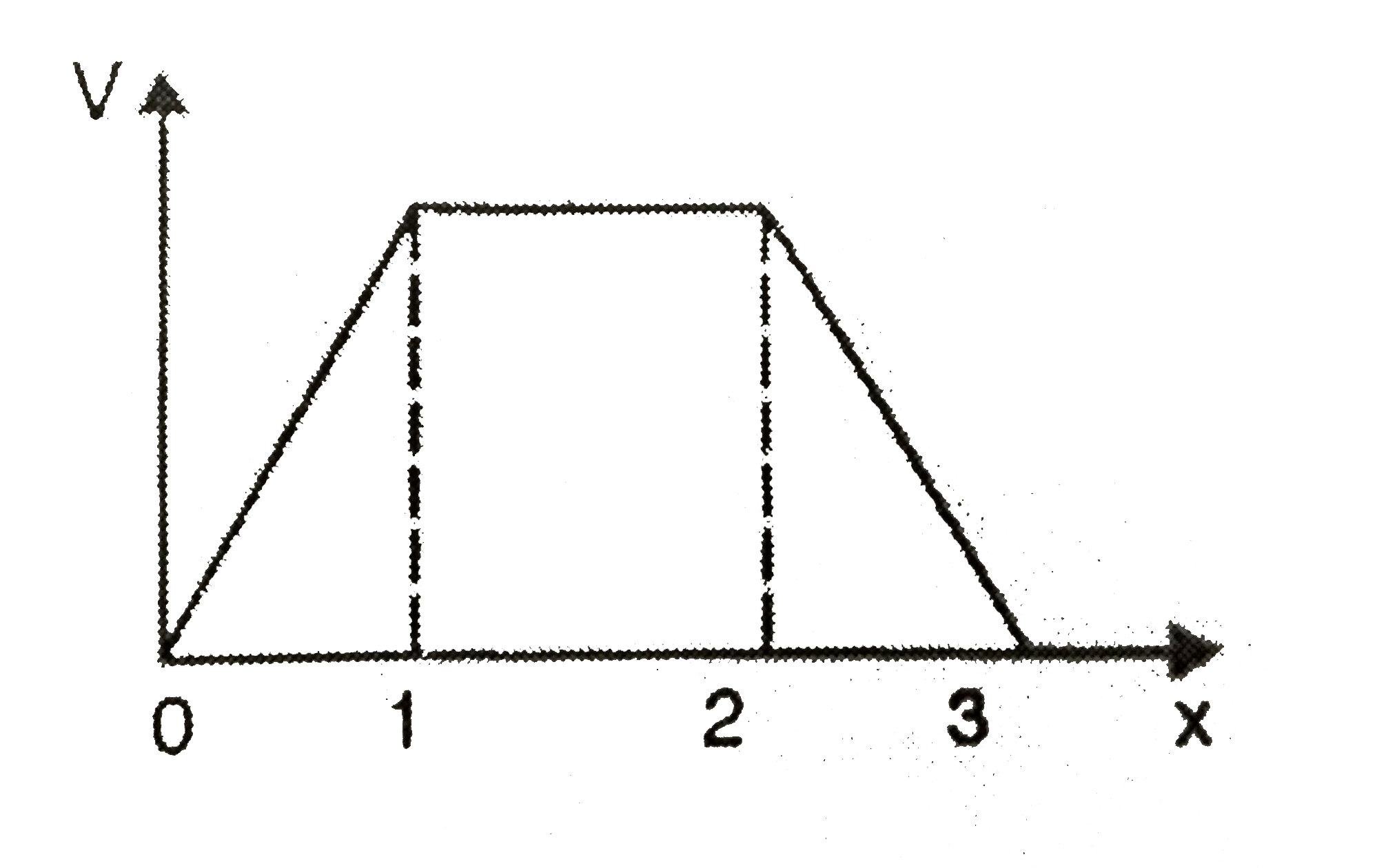
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V by a battery. Without disconnecting the battery, distance between the plates of capacitor is tripled and a dielectric medium of K = 10 is introduced between the plates of capacitor. Explain giving reasons how will the following be affected ?
(a) Capacitance of capacitor
(b) Charge on capacitor
(c ) Energy density of capacitor.
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionA parallel plate capacitor is charged to a potential difference of 10 volts. After disconnecting the battery, distance between the plates of capacitor is decreased by using nonconducting handles. The potential difference between the plates will
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionA parallel plate capacitor with air between the plates has capacitance of 9pF. The separation between its plates is 'd'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant k1=3 and thickness d3 while the other one has dielectric constant k2=6 and thickness 2d3. Capacitance of the capacitor is now
View SolutionA parallel plate capacitor with air between the plates has capacitance of 9pF. The separation between its plates is 'd'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant k1=3 and thickness d3 while the other one has dielectric constant k2=6 and thickness 2d3. Capacitance of the capacitor is now
View Solution