A portion of a tube is shown in the figure. Fluid is flowing from cross-section area A1 to A2. The two cross-sections are at distance 'l' from each other. The velocity of the fluid at section A2 is √gl2. If the pressures at A1 & A2 are same, then the angle made by the tube with the horizontal will be:
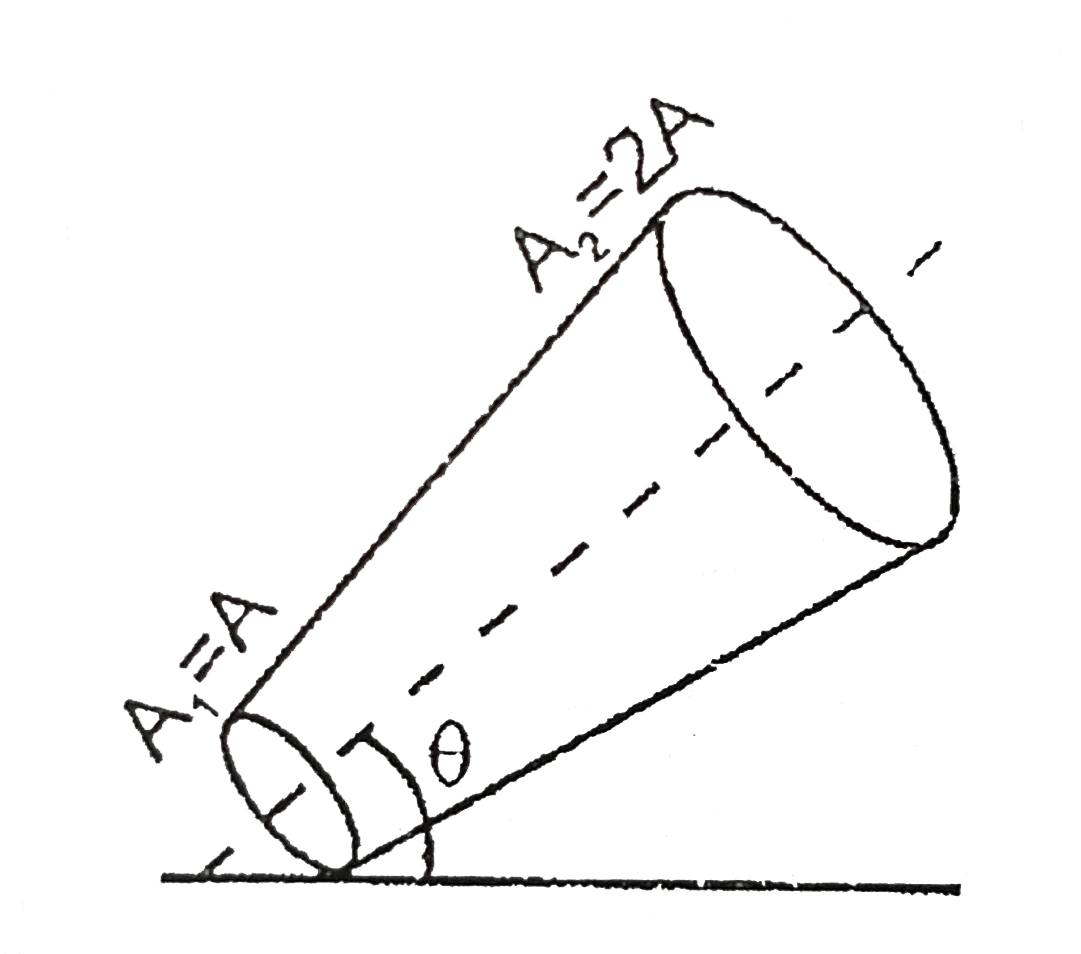
37∘
sin−1'34
53∘
cos−1'34
The correct Answer is:B
Step by step video & image solution for A portion of a tube is shown in the figure. Fluid is flowing from cross-section area A_(1) to A_(2). The two cross-sections are at distance 'l' from each other. The velocity of the fluid at section A_(2) is sqrt((gl)/(2)). If the pressures at A_(1) & A_(2) are same, then the angle made by the tube with the horizontal will be: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - II
6 Videos
- FLUID MECHANICSBOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - III
7 Videos
- FLUID MECHANICSBOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - II Section (C)
5 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise
52 Videos
- FULL TEST 1BOOK - RESONANCE ENGLISHCHAPTER - FULL TEST 1EXERCISE - Exercise
30 Videos
Similar Questions
Knowledge Check
An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
A9:4B3:2C√3:√2D√2:√3An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
A9:4B3:2C√3:√2D√2:√3A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The differnece in the levels of the liquid in the two vertical tubes is h. then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
If cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)

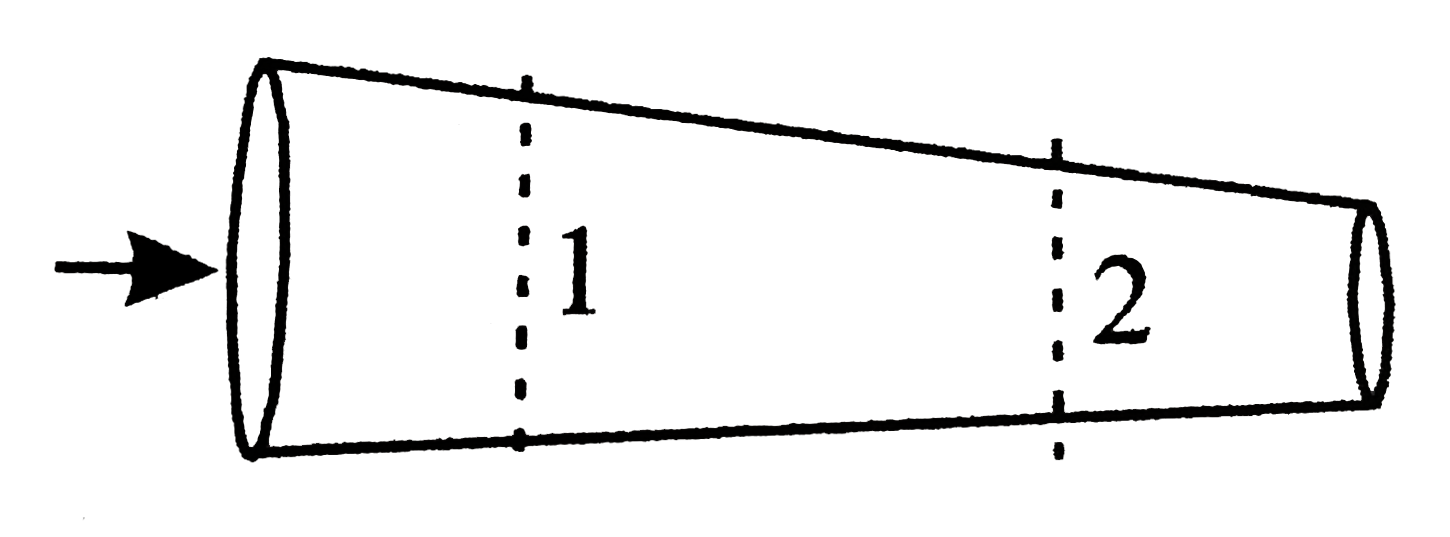
View SolutionA liquid flows in a tube from left to right as shown in figure. A1 and A2 are the cross-section of the portions of the tube as shown. Then the ratio of speeds v1/v2 will be

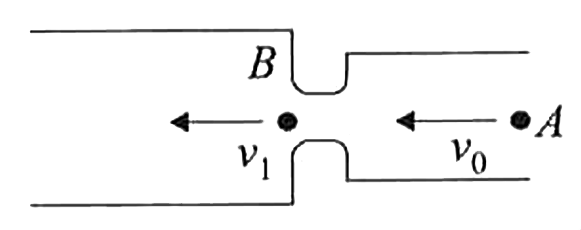
View SolutionThe velocity of an electron at point A1 is V0 where cross sectional area is A. The velocity of electron at the end of contraction at point B, where cross sectional area is 2A, is V1. Find the correct option:
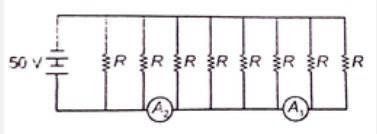
View SolutionIn the situation shown , the readings of ideal ammeters A1 and A2 are in the ratio.
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then

View Solution