The work done an a particle of mass by a force
(K being a constant of appropriate dimensions), when the partical is taken from the point (a,0) to the point (0,a) along a circular path of radius a about the origin in x - y plane is
zero
none
The correct Answer is:B
This force is tangential and constant magnitude done will be product of force and distance.
Topper's Solved these Questions
Similar Questions
Find the distance of the point (2,3) from the line 2x−3y+9=0 measured along a line x−y+1=0.
View SolutionThe maximum distance of the point (k,0) from the curve 2x2+y2−2x=0 is equal to
View SolutionIf the points (2, 1) and (1, −2) are equidistant from the point (x, y) , show that x+3y=0 .
View SolutionThe work done by the force F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown in
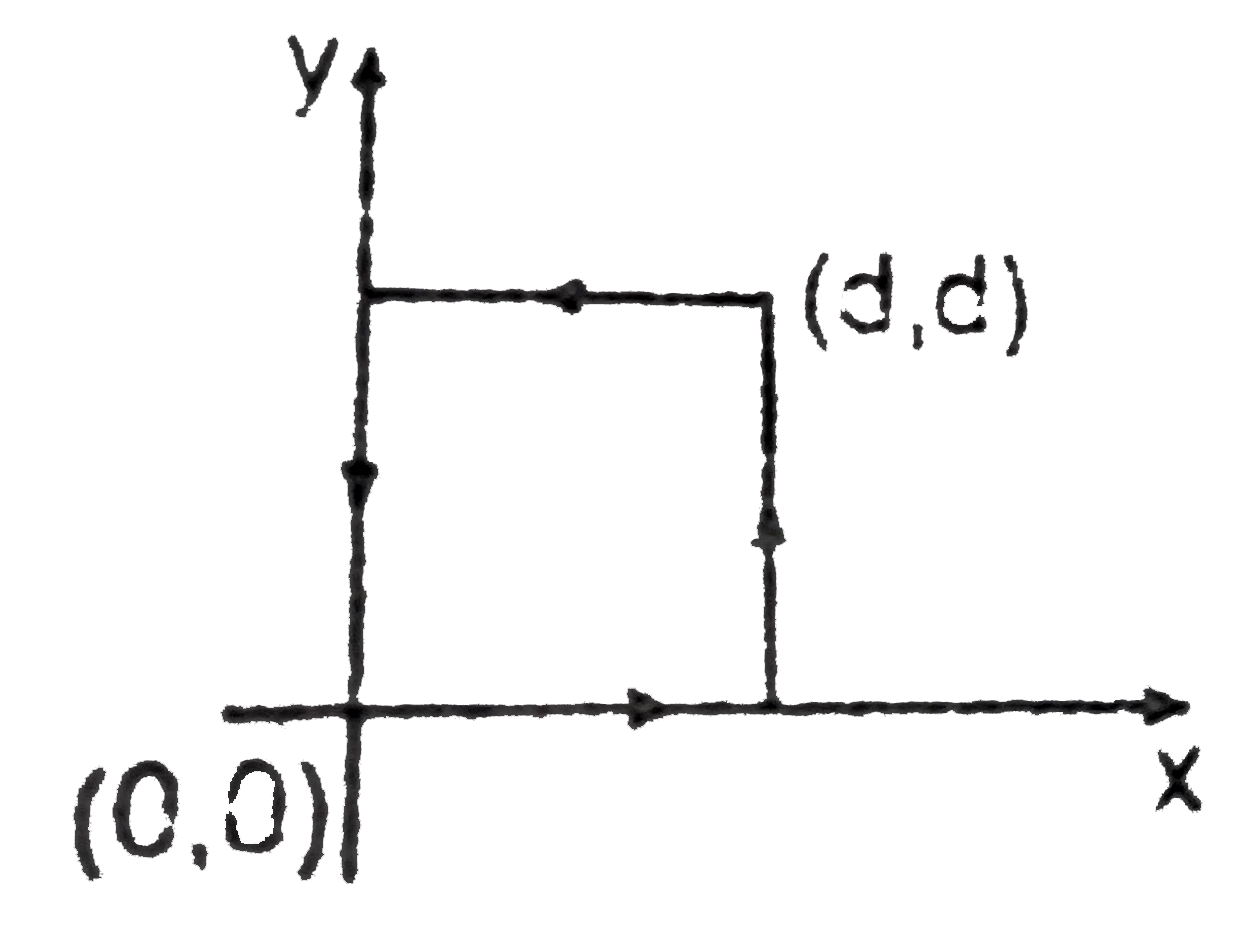 View Solution
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
View SolutionFind what the following equation become when the origin is shifted to the point (1,1): x2+xy−3x−y+2=0
View SolutionA particle of mass m and charge q is in a electric and magnetic field given by
→E=2ˆi+3ˆj,→B=4ˆj+6ˆk
The charged particle is shifted form the origin to the point P(x = 1, y=1) along a striaght path. The magnitude of the total work done is :View SolutionThe work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
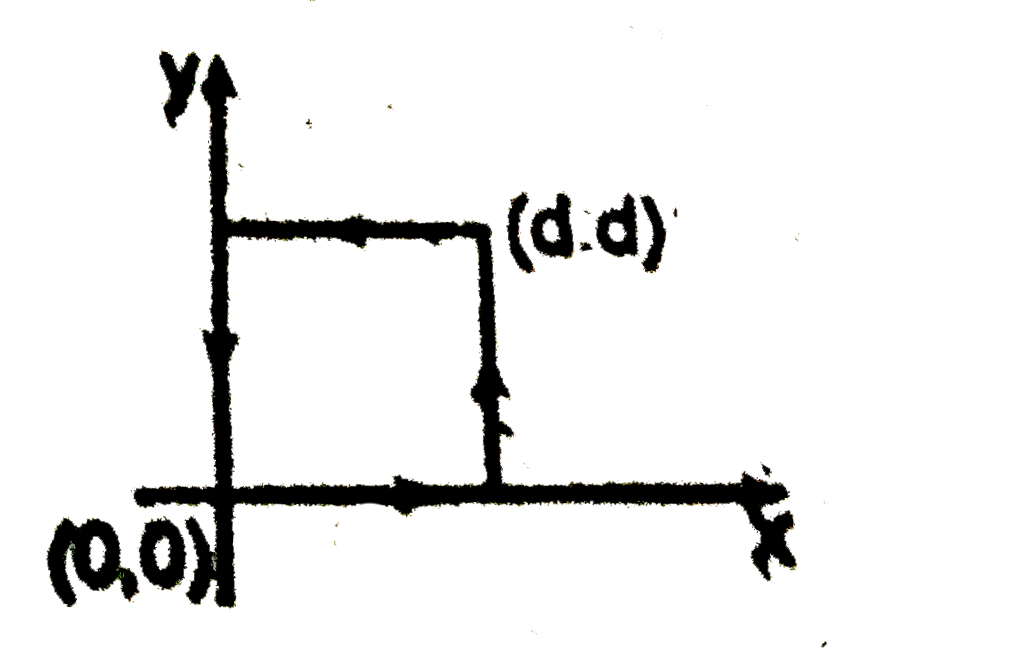 View Solution
View SolutionThe distance of the point (1,−2,4) from the plane passing through the point (1,2,2) perpendicular to the planes x−y+2z=3 and 2x−2y+z+12=0 is
View SolutionA particle is moved inx−y plane form (a,0) to (0,a) along circular arc having centre at origin. Work done by a force −ky(x2+y2)32ˆi+kx(x2+y2)32ˆj on the particle during this motion will be
View Solution

