A masonary column of density ρ has height h top cross sectional area A1 and bottom cross sectional area A2. Top cross sectional of the column is uniformly loaded with load F. If stress at any cross section of the column is same and ρghA1=2F, the integer closest to A2A1 is
To solve the problem, we need to analyze the forces acting on the masonry column and apply the concept of stress.
1. Understanding the Problem:
- We have a masonry column with density ρ, height h, top cross-sectional area A1, and bottom cross-sectional area A2.
- The top of the column is uniformly loaded with a force F.
- The condition given is ρghA1=2F, where g is the acceleration due to gravity.
2. Calculate the Weight of the Column:
- The weight of the column W can be expressed as:
W=Volume×Density=(A1⋅h)⋅ρg
- Thus, the weight of the column is:
W=ρghA1
3. Total Force on the Bottom Cross Section:
- The total force acting on the bottom cross-section A2 is the sum of the applied load F and the weight of the column:
Ftotal=F+W=F+ρghA1
4. Using the Given Condition:
- From the problem statement, we know:
ρghA1=2F
- Substituting this into the total force equation:
Ftotal=F+2F=3F
5. Stress at Cross Section A1:
- The stress σ1 at the top cross-section A1 is given by:
σ1=FA1
6. Stress at Cross Section A2:
- The stress σ2 at the bottom cross-section A2 is given by:
σ2=FtotalA2=3FA2
7. Equating the Stresses:
- According to the problem, the stress at any cross-section of the column is the same:
σ1=σ2
- Therefore, we have:
FA1=3FA2
8. Solving for the Ratio A2A1:
- Cancel F from both sides (assuming F≠0):
1A1=3A2
- Rearranging gives:
A2=3A1
- Thus, the ratio A2A1 is:
A2A1=3
9. Final Answer:
- The integer closest to A2A1 is 3.
- We have a masonry column with density ρ, height h, top cross-sectional area A1, and bottom cross-sectional area A2.
- The top of the column is uniformly loaded with a force F.
- The condition given is ρghA1=2F, where g is the acceleration due to gravity.
- The weight of the column W can be expressed as:
W=Volume×Density=(A1⋅h)⋅ρg
- Thus, the weight of the column is:
W=ρghA1
- The total force acting on the bottom cross-section A2 is the sum of the applied load F and the weight of the column:
Ftotal=F+W=F+ρghA1
- From the problem statement, we know:
ρghA1=2F
- Substituting this into the total force equation:
Ftotal=F+2F=3F
- The stress σ1 at the top cross-section A1 is given by:
σ1=FA1
- The stress σ2 at the bottom cross-section A2 is given by:
σ2=FtotalA2=3FA2
- According to the problem, the stress at any cross-section of the column is the same:
σ1=σ2
- Therefore, we have:
FA1=3FA2
- Cancel F from both sides (assuming F≠0):
1A1=3A2
- Rearranging gives:
A2=3A1
- Thus, the ratio A2A1 is:
A2A1=3
- The integer closest to A2A1 is 3.
Topper's Solved these Questions
Similar Questions
Will the height of the water column change if the cross section of the water column is made wider ?
View SolutionWater rises to a height h in a capillary tube of cross-sectional area A. the height to which water will rise in a capillary tube of cross-sectional area 4A will be
View SolutionWater rises to a height h in a capillary tube of cross-sectional area A. the height to which water will rise in a capillary tube of cross-sectional area 4A will be
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
 View Solution
View SolutionTwo similar wires under the same load yield elongation of 0.1mm and 0.05mm respectively. If the area of cross-section of the first wire is 4mm2, then the area of cross-section of the second wire is
View SolutionConsider a conductor of variable cross section in which current is flowing from cross section 1 to 2. Then
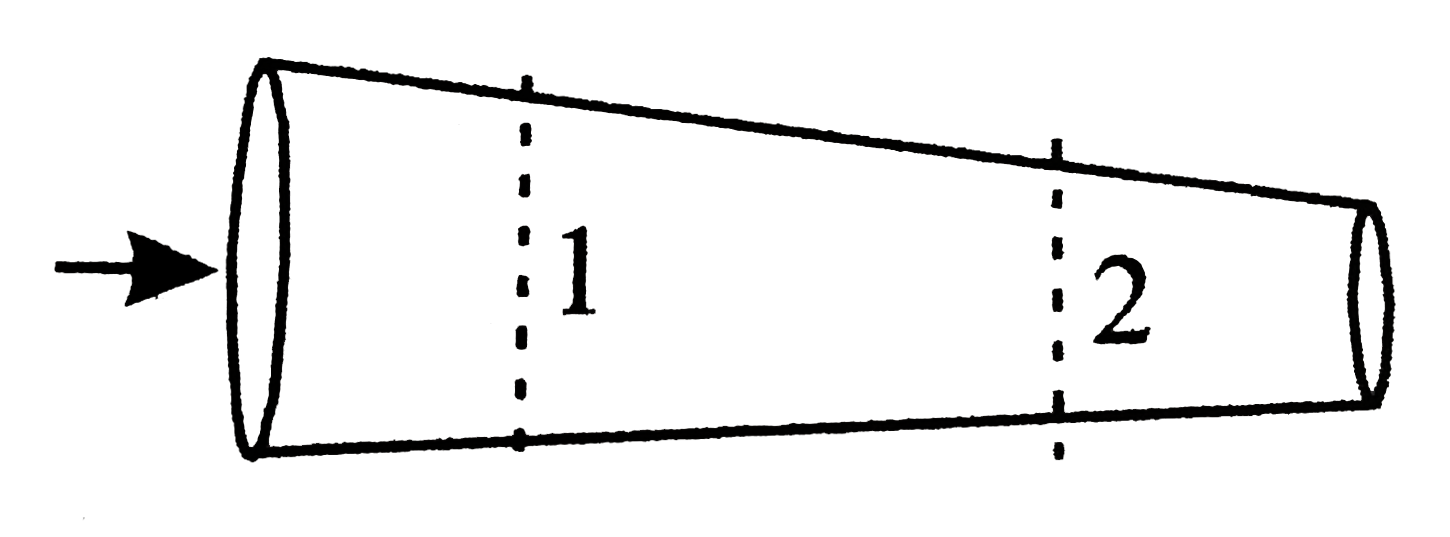 View Solution
View SolutionWhat force is applied on a piston of area of cross section 2cm2 to obtain a force 150 N on the piston of area of cross section 12cm2 in a hydraulic machine ?
View SolutionA uniform copper bar of density ρ , length L , cross - sectional area S and young's modulus Y is moving horizontally on a frictionless surface with constant acceleration a0. Find
(a) the stress at the center of the wire ,
(b) total elongation of the wire .View SolutionThe velocity of an electron at point A1 is V0 where cross sectional area is A. The velocity of electron at the end of contraction at point B, where cross sectional area is 2A, is V1. Find the correct option:
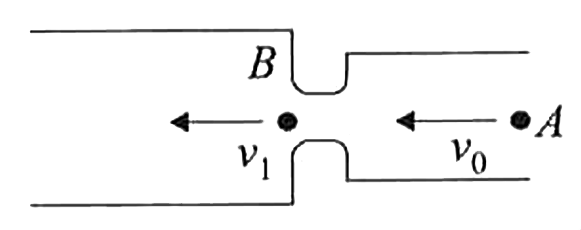 View Solution
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is
 View Solution
View Solution

