A convex lens is cut into two parts in different ways that are arranged in four manners, as shown. Which arrangement will give maximum optical power?
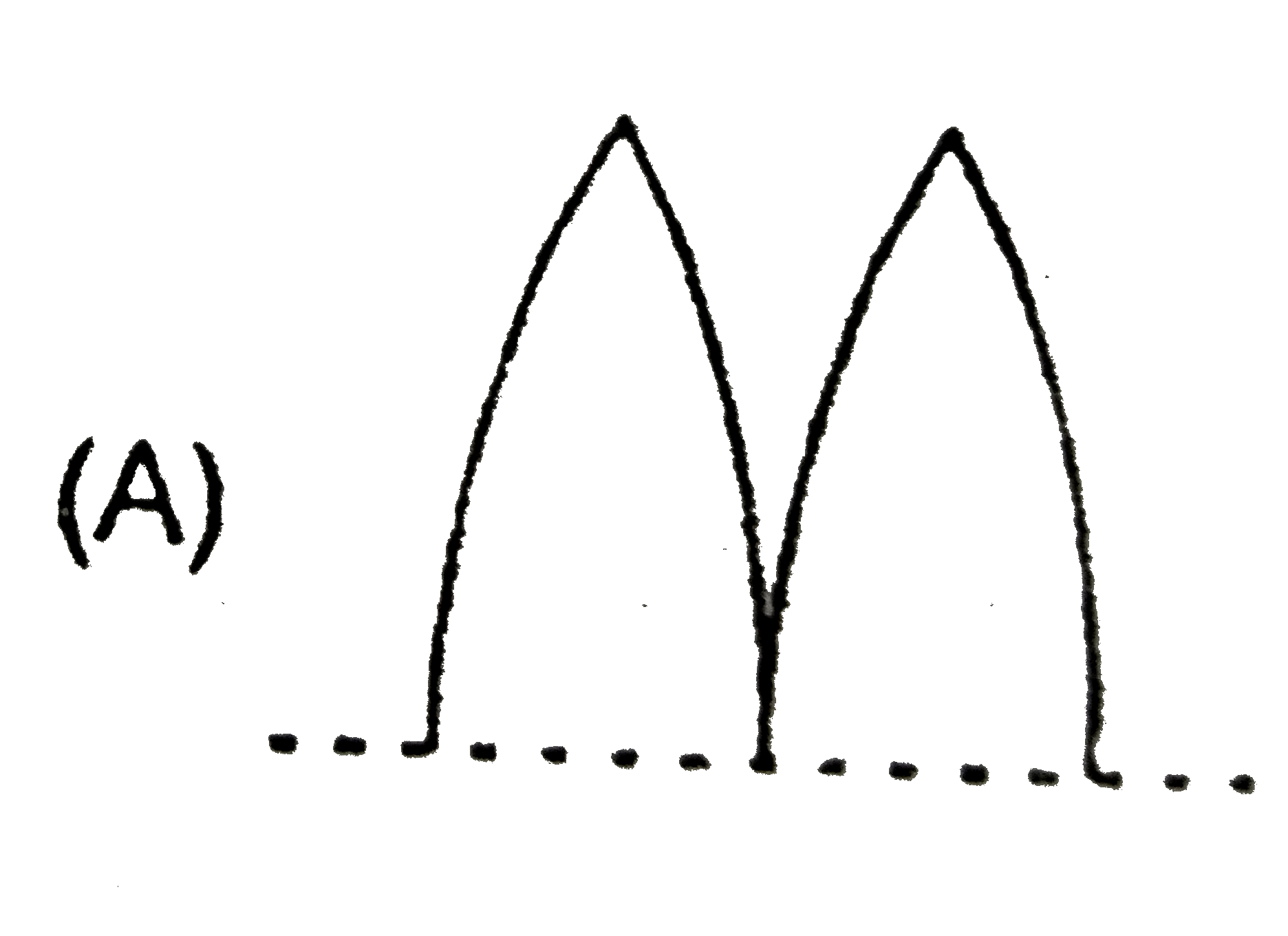

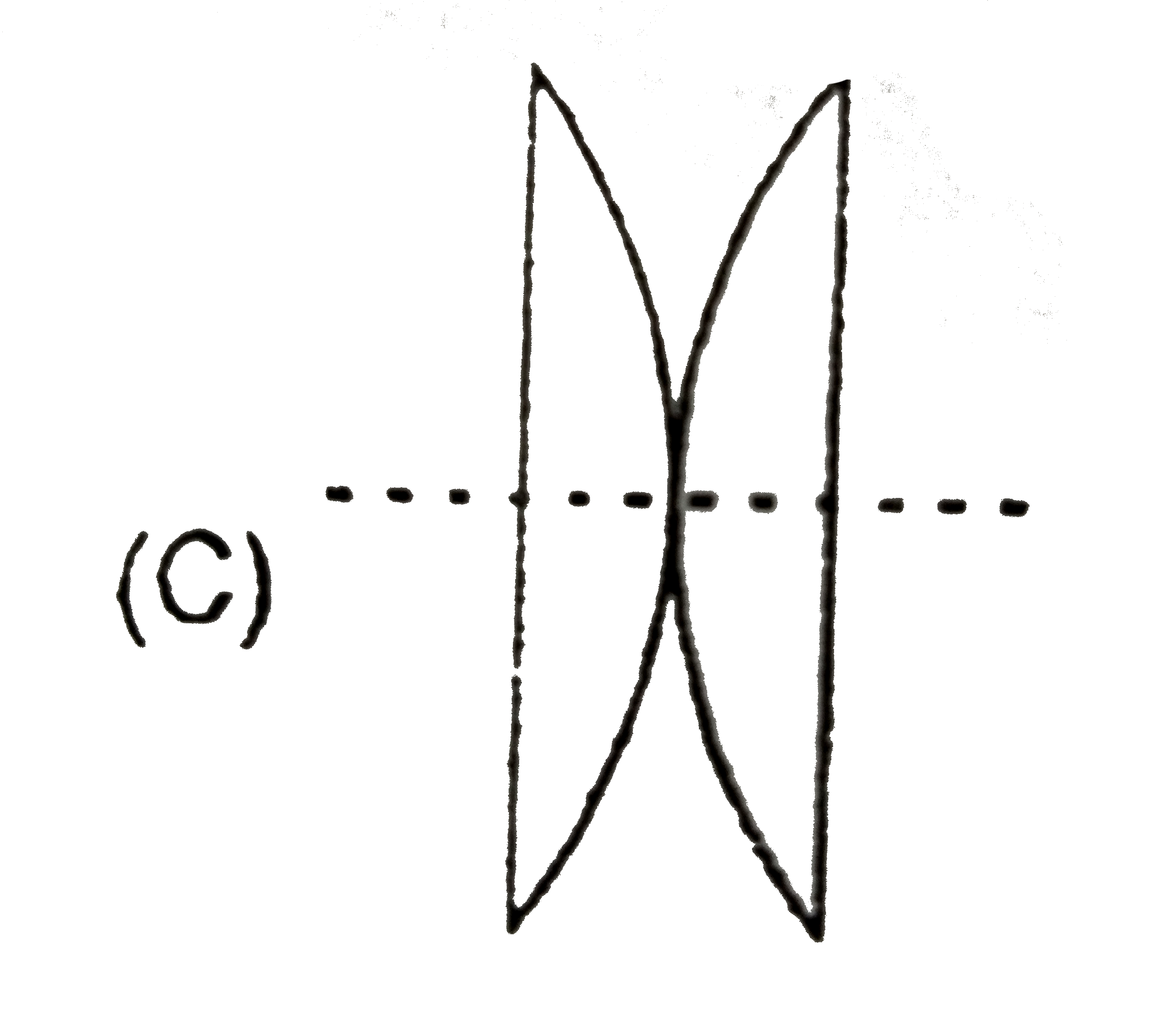

The correct Answer is:A
To determine which arrangement of the cut convex lens gives the maximum optical power, we will analyze the focal lengths of each arrangement and calculate their respective powers. The power P of a lens is given by the formula:
P=1f
where f is the focal length of the lens. The goal is to find the arrangement with the minimum focal length, as this will correspond to the maximum optical power.
1. Understanding the Lens Arrangement:
The convex lens is cut into two parts in different ways, and we need to analyze four different arrangements.
2. Power and Focal Length Relationship:
Recall that the power of a lens is inversely proportional to its focal length. Thus, to maximize the power, we need to minimize the focal length.
3. Analyzing Each Arrangement:
- Arrangement 1:
- The two parts of the lens are arranged such that they work together. The effective focal length f1 can be calculated as:
\frac{1}{f_1} = \frac{1}{f_1'} + \frac{1}{f_2'} \quad \text{(where f_1' and f_2' are the focal lengths of each half)}
- For equal halves of a lens, if the original lens had a focal length f, then each half will have a focal length of f2. Thus:
1f1=2f/2=4f⇒f1=f4
- Arrangement 2:
- In this arrangement, one part acts like a mirror. Thus, the effective focal length f2 becomes infinite, leading to:
P_2 = 0 \quad \text{(since f_2 = \infty )}
- Arrangement 3:
- The two parts are arranged such that they are still effective. The effective focal length f3 can be calculated similarly:
1f3=1f/2+1f/2=4f⇒f3=f4
- Arrangement 4:
- The two parts are arranged oppositely. The effective focal length f4 can be calculated as:
1f4=1f/2−1f/2=0⇒f4=∞
4. Calculating Powers:
- For Arrangement 1 and 3, f=f4:
P1=P3=4f
- For Arrangement 2 and 4, f=∞:
P2=P4=0
5. Conclusion:
The arrangements that yield the maximum optical power are Arrangement 1 and Arrangement 3, both having the same focal length and thus the same power. Therefore, the arrangement that gives maximum optical power is Arrangement 1 (or 3).
Final Answer:
Arrangement 1 gives the maximum optical power.
The convex lens is cut into two parts in different ways, and we need to analyze four different arrangements.
Recall that the power of a lens is inversely proportional to its focal length. Thus, to maximize the power, we need to minimize the focal length.
- Arrangement 1:
- The two parts of the lens are arranged such that they work together. The effective focal length f1 can be calculated as:
\frac{1}{f_1} = \frac{1}{f_1'} + \frac{1}{f_2'} \quad \text{(where f_1' and f_2' are the focal lengths of each half)}
- For equal halves of a lens, if the original lens had a focal length f, then each half will have a focal length of f2. Thus:
1f1=2f/2=4f⇒f1=f4
- In this arrangement, one part acts like a mirror. Thus, the effective focal length f2 becomes infinite, leading to:
P_2 = 0 \quad \text{(since f_2 = \infty )}
- The two parts are arranged such that they are still effective. The effective focal length f3 can be calculated similarly:
1f3=1f/2+1f/2=4f⇒f3=f4
- The two parts are arranged oppositely. The effective focal length f4 can be calculated as:
1f4=1f/2−1f/2=0⇒f4=∞
- For Arrangement 1 and 3, f=f4:
P1=P3=4f
- For Arrangement 2 and 4, f=∞:
P2=P4=0
The arrangements that yield the maximum optical power are Arrangement 1 and Arrangement 3, both having the same focal length and thus the same power. Therefore, the arrangement that gives maximum optical power is Arrangement 1 (or 3).
Arrangement 1 gives the maximum optical power.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
Find the number of ways in which 12 different beads can be arranged to form a necklace.
View SolutionIf a symmetrical bi-concave thin lens is cut into two identical halves, and they are placed in different ways as shown, then

View SolutionFind the number of ways in which 10 different diamonds can be arranged to make a necklace.
View SolutionIn the figure (i) a thin lens of focal length 10cm is shown. The lens is cut into two equal parts, and the parts are arranged as shown in the figure (ii). An object AB of height 1cm is placed at distance of 7.5cm from the arrangement. The height of the final image will be:
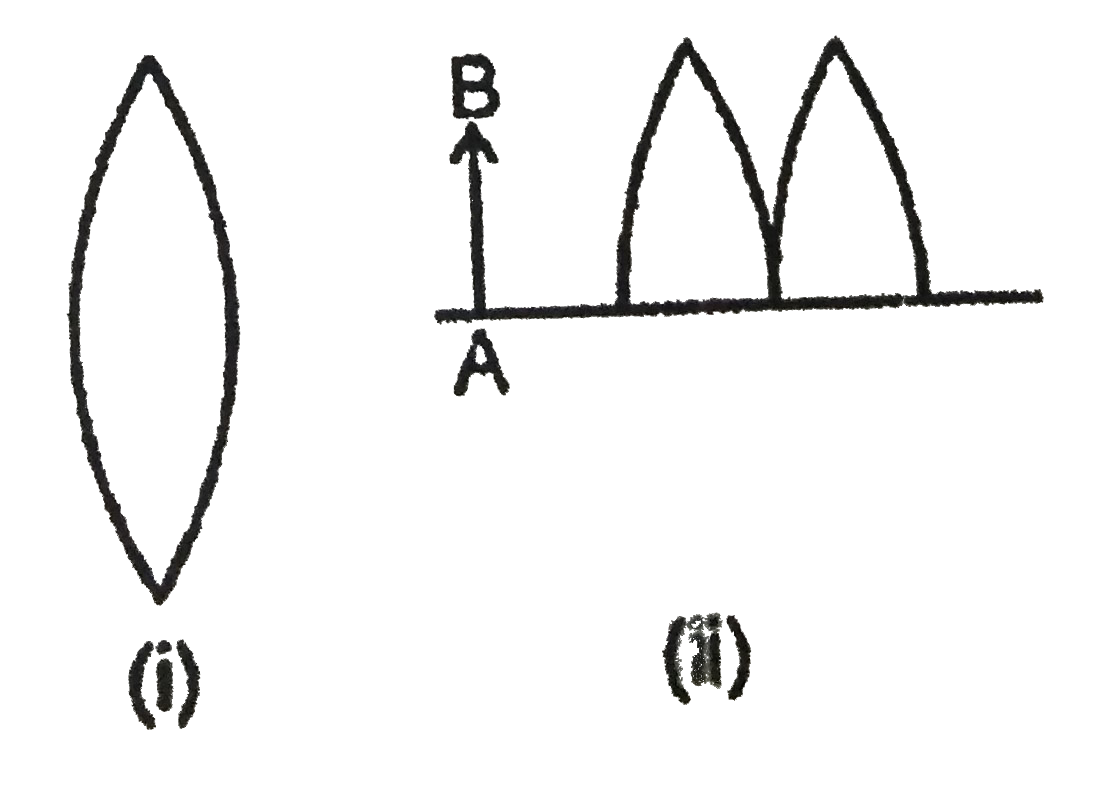
View SolutionA convex lens of glass (μ=1.5) is formed by combining two surfaces of radii R1=60cm and R2=30cm . It is cut into two parts in two different ways as shown in Figure .
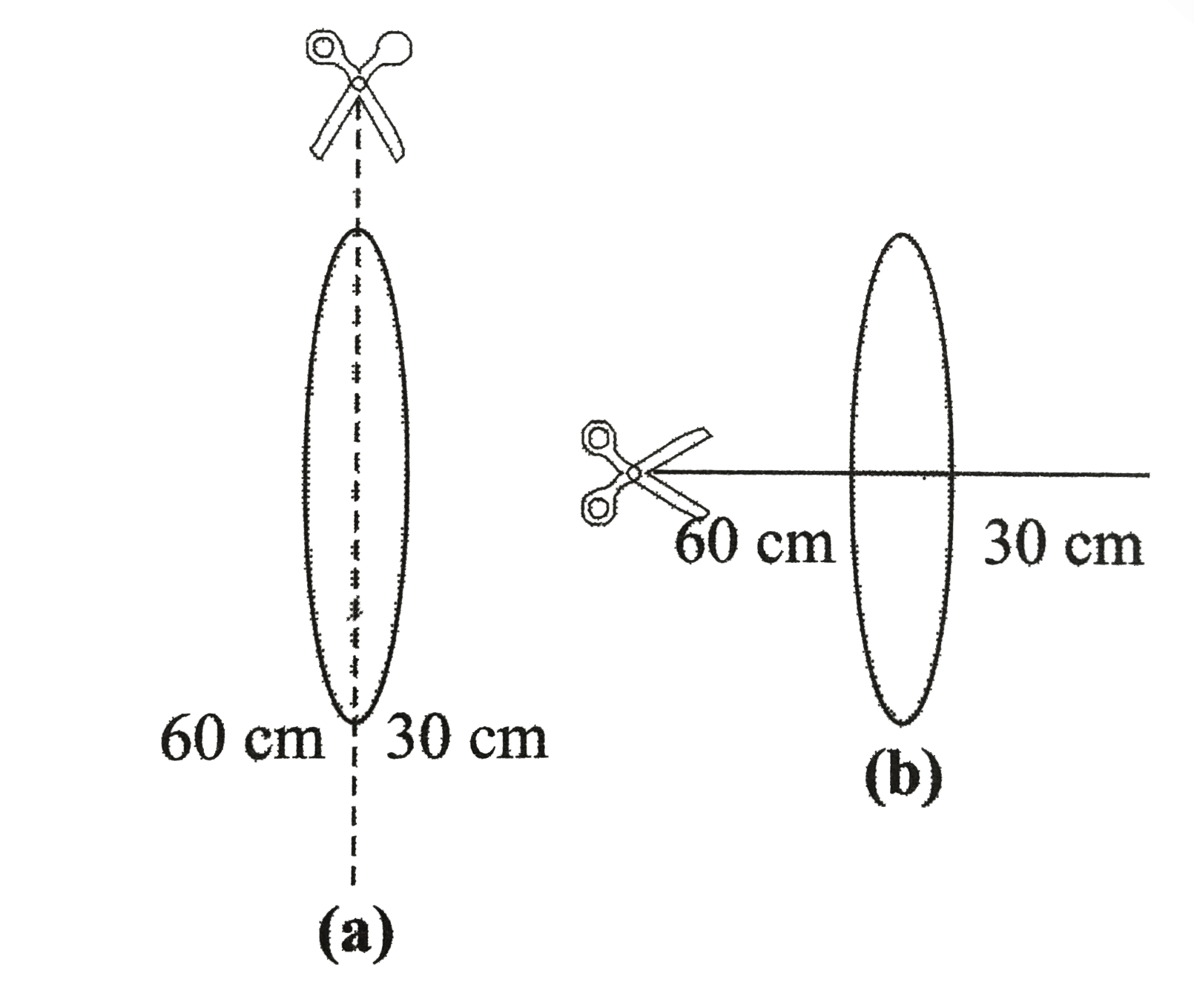
Find:
a. the focal length of the lens.
b. in figure (a), the focal length of left portion and that of the right portion.
c. in figure (b), the focal length of the upper part and that of the lower part.
View SolutionTwo displacement vectors of same magnitude are arranged in the folllowing manner.

Magnitude of resultant is maximum for
View SolutionA man thinks about 4 arrangements as shown to raise two small bricks each having mass m. Which of the arrangement would take minimum time ?
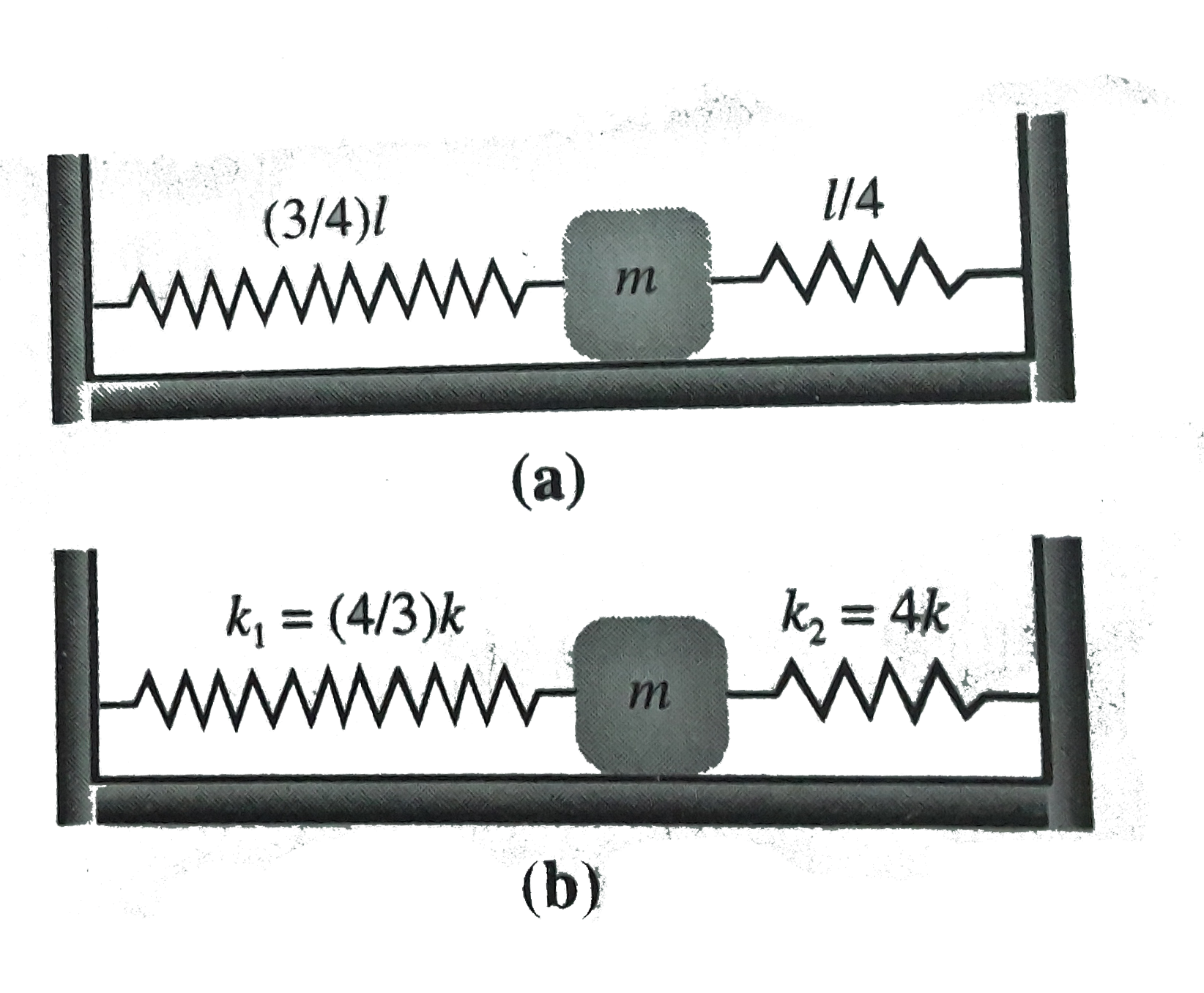
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
View SolutionGive two different ways by which the product can be separated from the reactants.
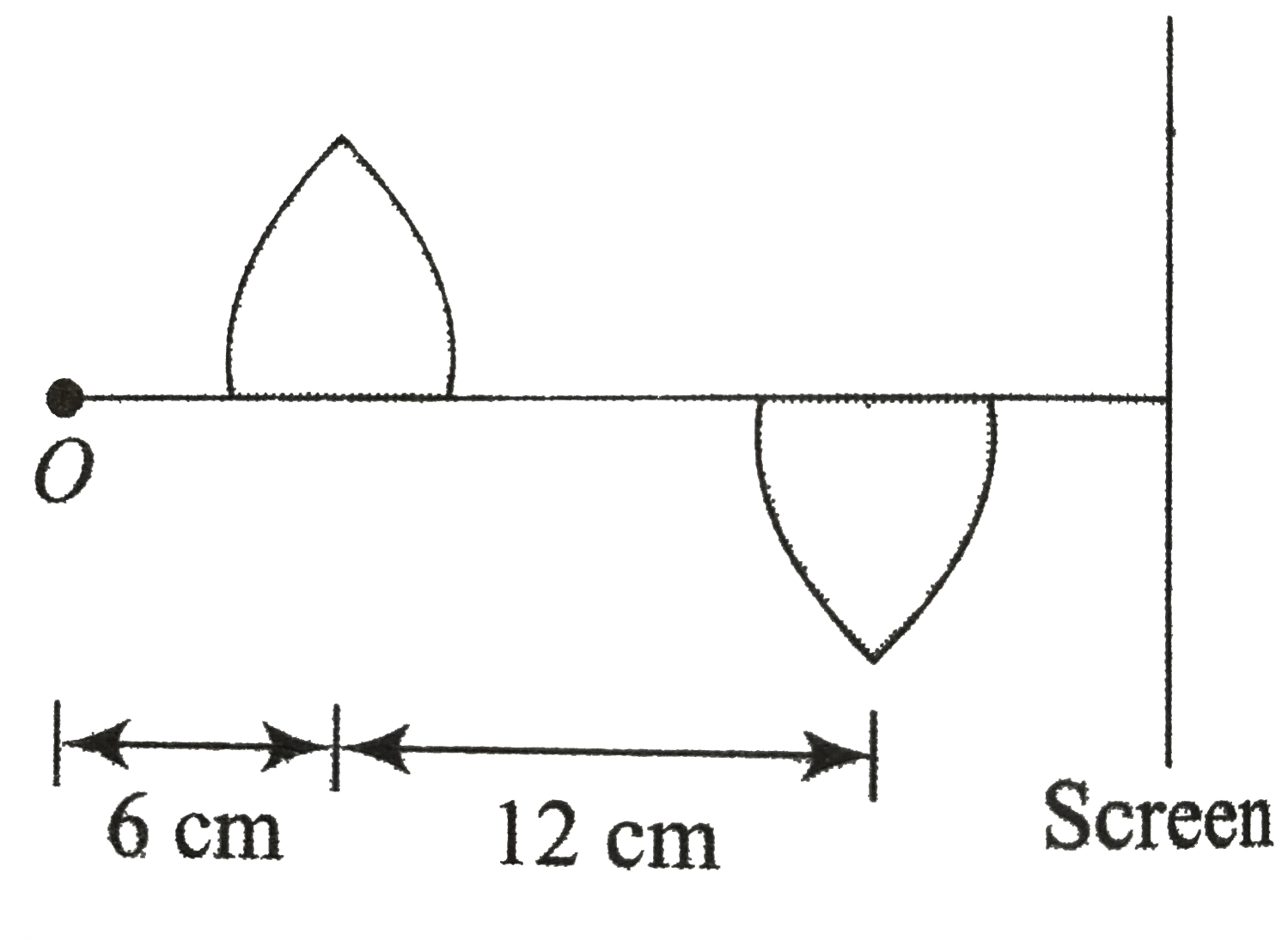
View SolutionA convex lens is cut in half along its principal axis and the two halves are separated by a distance of 12cm. An object is placed 6cm in front of the lens as shown in Figure., Two sharp images are formed on the screen placed 80cm from the object. What is the focal length of the lens?
View Solution
