In the fraunhaufer differaction from a single slit illuminated by polychromatic light, the first minimum with wavelength λ1 is found to be coincident with the third minimum at λ2. Then find the value of λ1λ2
The correct Answer is:3
To solve the problem, we need to analyze the conditions for the minima in a single-slit diffraction pattern. The first minimum for a wavelength λ1 coincides with the third minimum for a wavelength λ2.
1. Understanding the Position of Minima:
The position of the minima in a single-slit diffraction pattern is given by the formula:
yn=nλDd
where yn is the position of the nth minimum, λ is the wavelength of the light, D is the distance from the slit to the screen, and d is the width of the slit.
2. Setting Up the Equations:
- For the first minimum with wavelength λ1:
y1=1⋅λ1Dd
- For the third minimum with wavelength λ2:
y3=3⋅λ2Dd
3. Equating the Positions:
Since the first minimum of λ1 coincides with the third minimum of λ2, we can set the two equations equal to each other:
λ1Dd=3λ2Dd
4. Cancelling Common Terms:
We can cancel D and d from both sides (assuming D and d are not zero):
λ1=3λ2
5. Finding the Ratio:
To find the ratio λ1λ2:
λ1λ2=3
Final Answer:
λ1λ2=3
The position of the minima in a single-slit diffraction pattern is given by the formula:
yn=nλDd
where yn is the position of the nth minimum, λ is the wavelength of the light, D is the distance from the slit to the screen, and d is the width of the slit.
- For the first minimum with wavelength λ1:
y1=1⋅λ1Dd
- For the third minimum with wavelength λ2:
y3=3⋅λ2Dd
Since the first minimum of λ1 coincides with the third minimum of λ2, we can set the two equations equal to each other:
λ1Dd=3λ2Dd
We can cancel D and d from both sides (assuming D and d are not zero):
λ1=3λ2
To find the ratio λ1λ2:
λ1λ2=3
λ1λ2=3
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A slit of width a is illuminiated by white light. The first diffraction minimum for light of λ=6500Å is formed at θ=30∘, then the width a of the slit is
View SolutionA single slit of width d is placed in the path of beam of wavelength λ. The angular width of the principal maximum obtained is-
View SolutionThe KE of the photoelectrons is E when the incident wavelength is λ2. The KE becomes 2E when the incident wavelength is λ3. The work function of the metal is
View SolutionIn a Young's double slit experiment with slit separation 0.1 mm, one observes a bright fringe at angle 140 rad by using light of wavelength λ1. When the light of wavelength λ2 is used a bright fringe is seen at the same angle in the same set up. Given that λ1andλ2 are in visible range (380 nm to 740 nm), their values are :
View Solution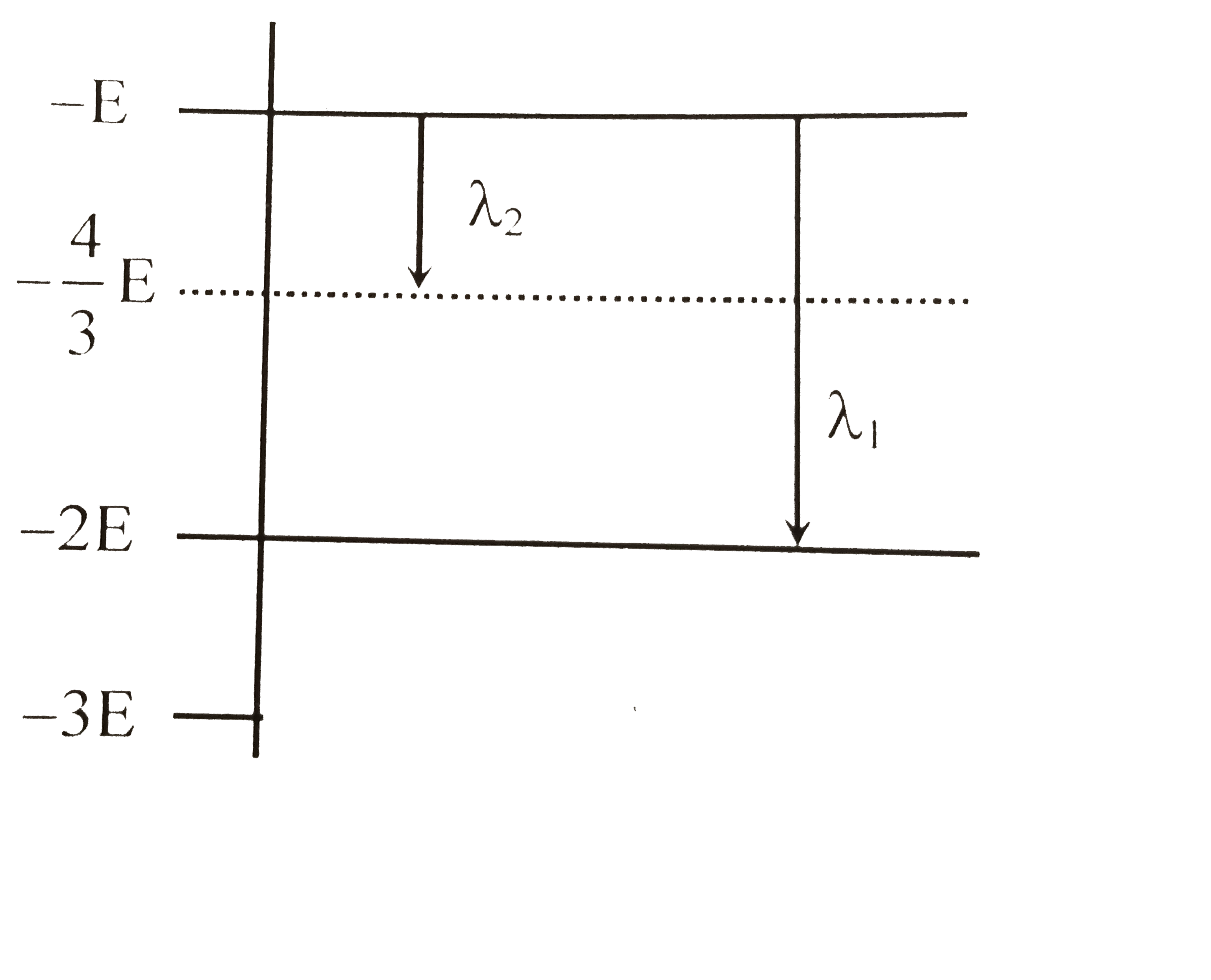
Some energy levels of a molecule are shown in the figure. The ratio of the wavelength r=λ1λ2,is given by:
View SolutionV1 and V2 are the stopping potentials for the incident radiations of wave lengths λ1 and λ2 respectively are incident on a metallic surface. If λ1=3λ2 then
View SolutionA radioactive nucleus can decay be either emitting an α particle or by emitting a β particle. Probability of α decay is 75% while that of β decay is 25% the decayconstatnt of α decay is λ1 and that of β decay is λ2 is λ1λ2
View SolutionLi2+ is initially is ground state. When radiation of wavelength λ0 incident on it, it emits 6 different wavelengths during de excitation find λ0
View SolutionLi2+ is initially is ground state. When radiation of wavelength λ0 incident on it, it emits 6 different wavelengths during de excitation find λ0
View Solution(a) Why are coherent sources necessary to produce a sustained interference pattern ?
(b) In Young's double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
View Solution
