The block of mass m1 and m2 are connected with a spring of netural length l and spring constant k. The systeam is lying on a smoth horizontal surface. Initially spring is compressed by x0 as shown in figure.

Show that the two blocks will perform SHM about their equilibrium position. Also (a) find the time period, (b) find amplitude of each block and (c) length of spring as a funcation of time.
(a) Hence both the blocks will be in equilibrium at the same time when spring is in its natural length. Let EP1 and EP2 be equilibrium positions of block A and B as shown in figure.
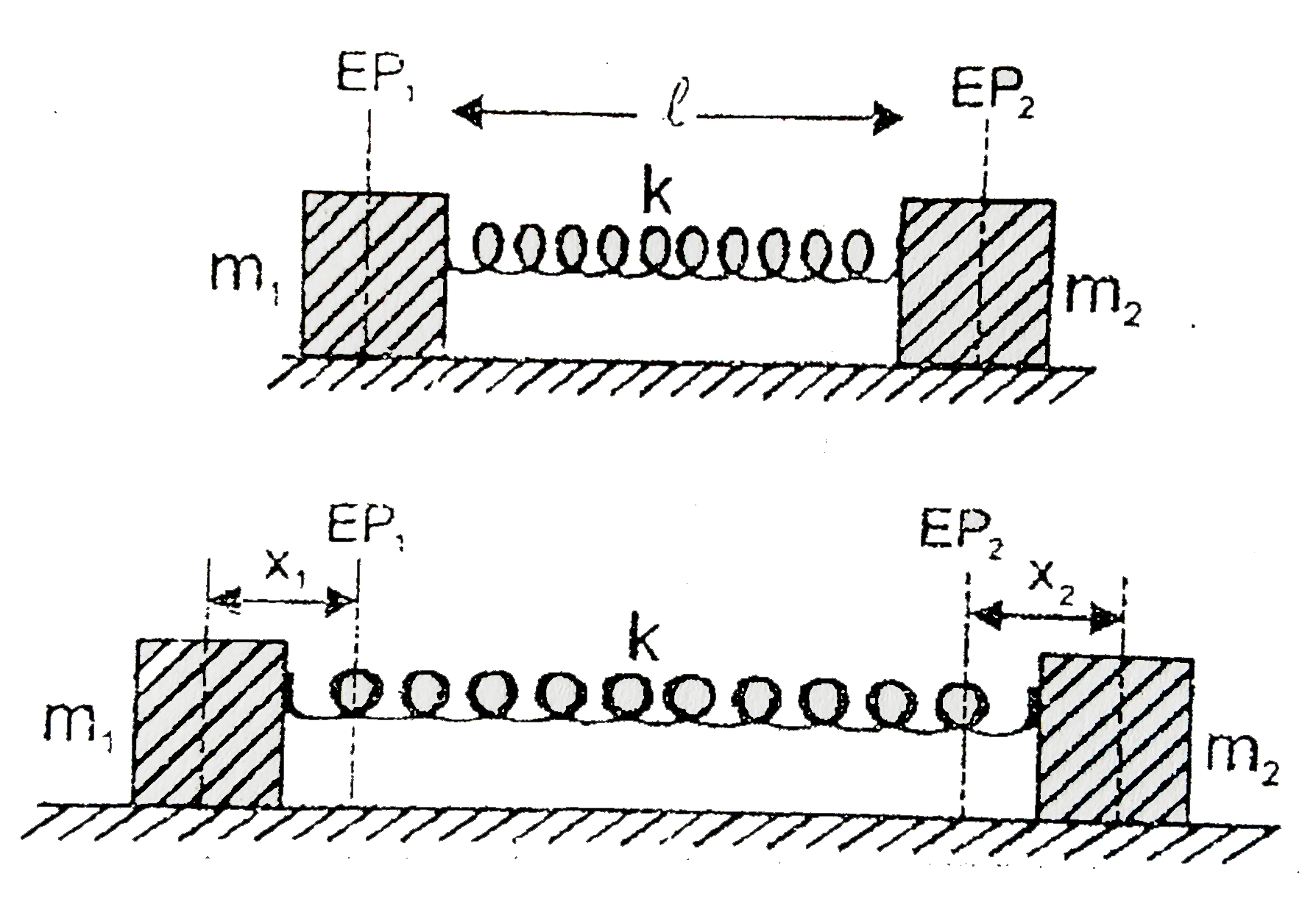
Let at any time during oscillations, blocks are at a distance of x1 and x2 from their equilibrium positions.
As no external force is acting on the spring on the spring block systeam
∴(m1+m2)Δxcm=m1x1−m2x2=0 or m1x1−m2x2
for 1st particle, force equation can be written as
k(x1+x2)=−m1d2x1dt2 or k(x1+m1m2x1)=−m1a1
or, a1=−k(m1+m2)m1m2x1∴ω2=k(m1+m2)m1m2
Hence, T=2π√m1m2k(m1+m2)=2p√μK where μ='m1m2(m1+m2) which is known as reduced mass
Ans (a)
Similarly time period of 2nd particle can be found. Both will be having the same time period.
(b) Let the amplitude of blocks be A1 and A2.
m1A1=m2A2
By energy conservation,
12k(A1+A2)2=12kx20 or, A1+A2=x0
or, A1+A2=x0 or, A1+m1m2A1=x0
or, A1=m2x0m1+m2 similarly, A2=m1x0m1+m2
(c) Consider equilibrium position of 1st particle as origin, i.e. x=0.
x co-ordinate of particles can be written as
x1A1cosωt and x2=l−A2cosωt
length =x2−x1
=l−(A1+A2)cosωt

Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Solved Miscellaneous Problems
9 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionFind the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is upstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View Solution
