In the above problem if block is released from there, what would be maximum extension.
To find the maximum extension of the block when it is released, we can use the principle of conservation of energy. Here's a step-by-step solution:
Step 1: Understand the System
We have a block attached to a spring. When the block is released from a certain height, it will fall under the influence of gravity and stretch the spring. The maximum extension occurs when all the gravitational potential energy has been converted into elastic potential energy in the spring.
Step 2: Set Up the Energy Conservation Equation
At the point of maximum extension, the gravitational potential energy (GPE) of the block is equal to the elastic potential energy (EPE) stored in the spring.
- The gravitational potential energy when the block is at maximum extension x0 is given by:
GPE=mgx0
where m is the mass of the block, g is the acceleration due to gravity, and x0 is the maximum extension.
- The elastic potential energy stored in the spring at maximum extension is given by:
EPE=12kx20
where k is the spring constant.
Step 3: Write the Conservation of Energy Equation
Setting the gravitational potential energy equal to the elastic potential energy, we have:
mgx0=12kx20
Step 4: Rearrange the Equation
Rearranging the equation to isolate x0:
12kx20−mgx0=0
Step 5: Factor the Equation
Factoring out x0:
x0(12kx0−mg)=0
This gives us two solutions:
1. x0=0 (the trivial solution)
2. 12kx0−mg=0
Step 6: Solve for Maximum Extension x0
From the second equation, we can solve for x0:
12kx0=mg
x0=2mgk
Conclusion
The maximum extension x0 of the spring when the block is released is:
x0=2mgk
We have a block attached to a spring. When the block is released from a certain height, it will fall under the influence of gravity and stretch the spring. The maximum extension occurs when all the gravitational potential energy has been converted into elastic potential energy in the spring.
At the point of maximum extension, the gravitational potential energy (GPE) of the block is equal to the elastic potential energy (EPE) stored in the spring.
GPE=mgx0
where m is the mass of the block, g is the acceleration due to gravity, and x0 is the maximum extension.
EPE=12kx20
where k is the spring constant.
Setting the gravitational potential energy equal to the elastic potential energy, we have:
mgx0=12kx20
Rearranging the equation to isolate x0:
12kx20−mgx0=0
Factoring out x0:
x0(12kx0−mg)=0
1. x0=0 (the trivial solution)
2. 12kx0−mg=0
From the second equation, we can solve for x0:
12kx0=mg
x0=2mgk
The maximum extension x0 of the spring when the block is released is:
x0=2mgk
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I
25 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
A block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View SolutionEnergy released per gram would be
View SolutionIn the above problem, direction of friction force is
View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass 2m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched. Find the maximum extension in the spring and acceleration of block B at time of maximum extension
 .
.
View SolutionA block of mass 1kg is kept on the tilted floor of a lift moving down with acceleration 3ms−2. If the block is released from rest as shown, what will be the time taken by block to reach the bottom? What is the normal reaction on the block during the motion?

View SolutionIn the above problem, the maximum positive displacement x is
View SolutionIn figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
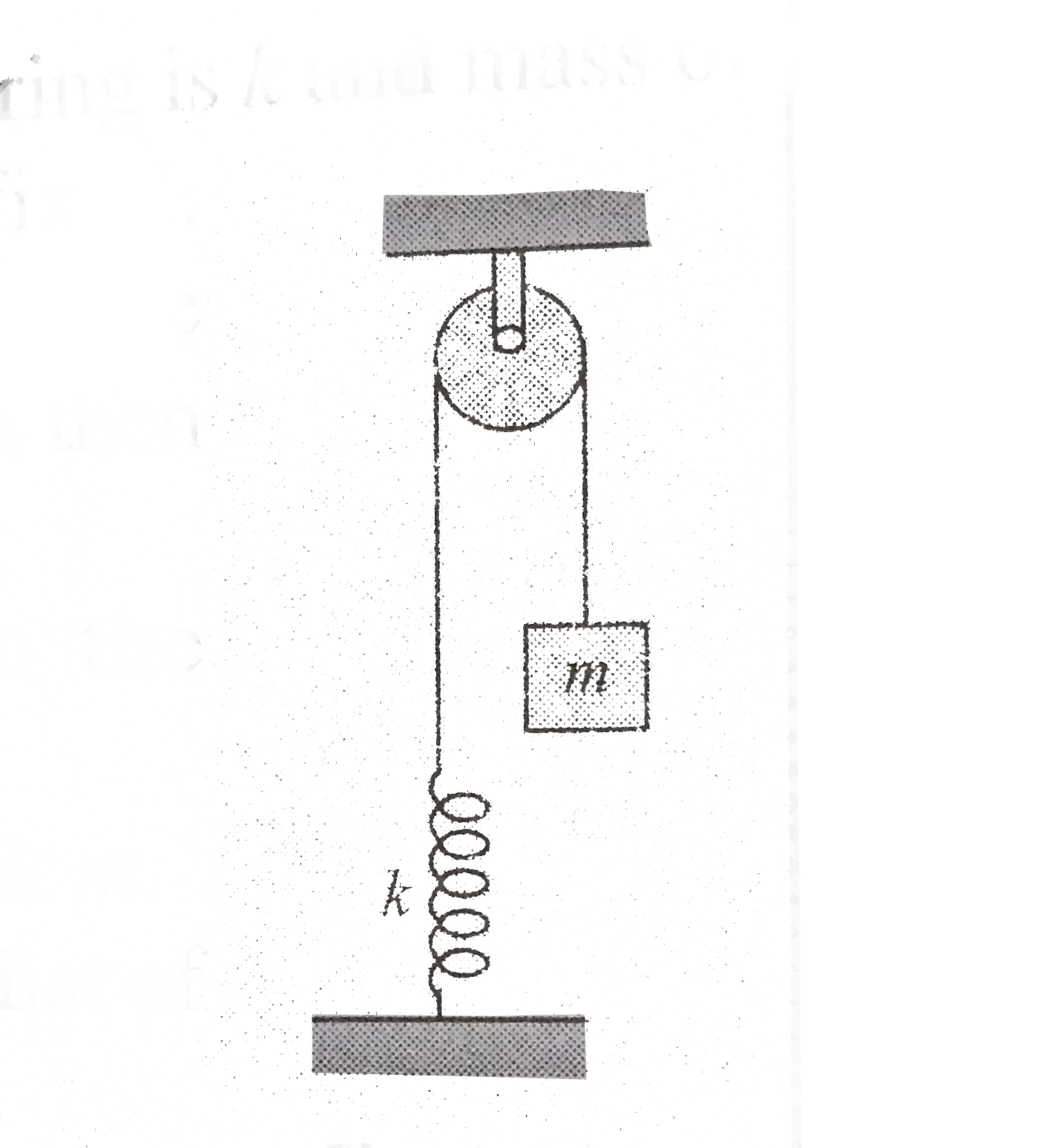
View SolutionIn the above problem the displacement after 2 s is:
View SolutionConsider the situation shown in figure.
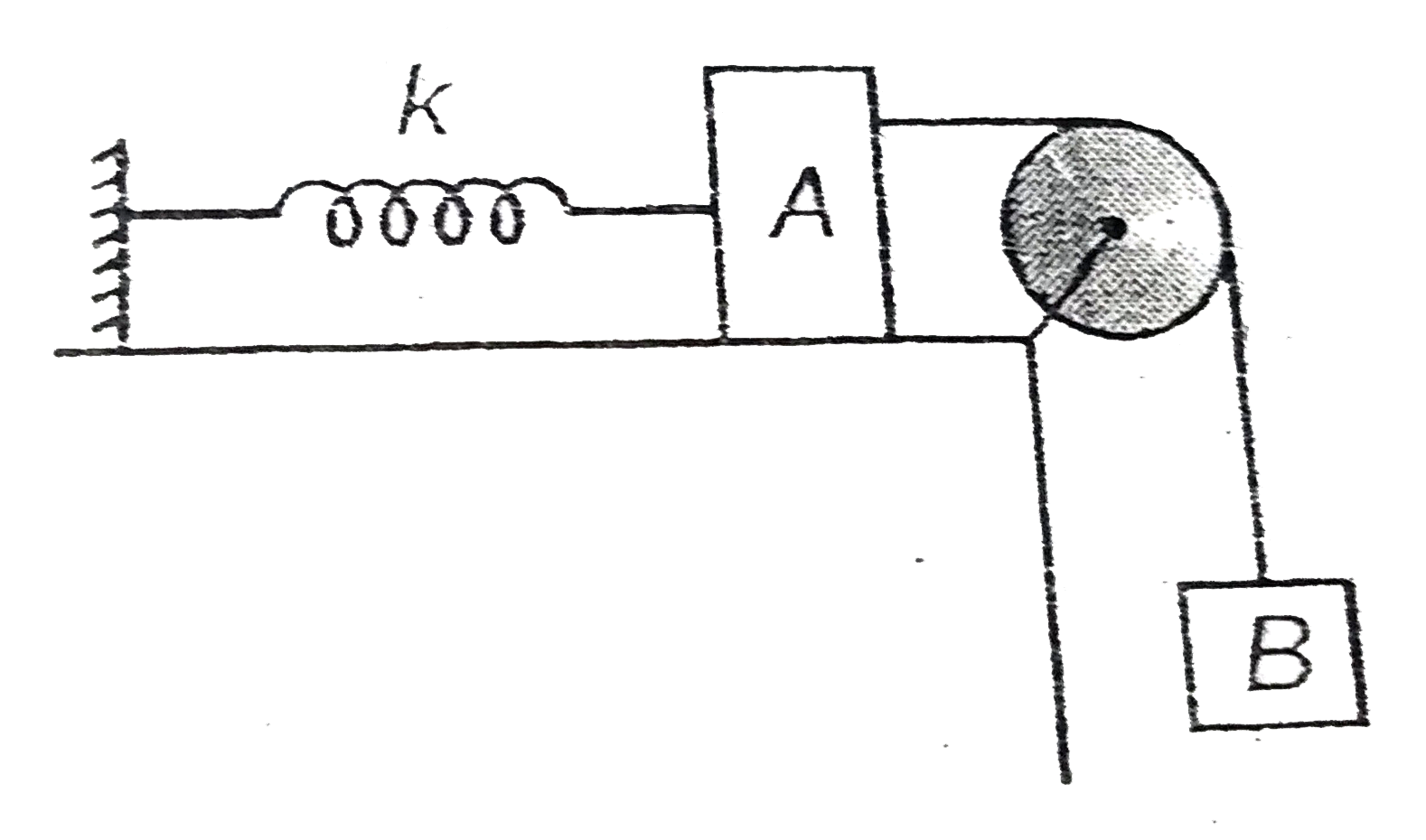
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.

View Solution
