A square conducting loop of side L is situated in gravity free space. A small conducting circular loop of radius r(r<<L) is placed at the center of the square loop, with its plane perpendicular to the plane of the square loop. The mutual inductance of the two coils is
2√2μ0ILr2
2√2μ0I0Lr2
zero
None of these
To find the mutual inductance M of a square conducting loop and a small circular conducting loop placed at its center, we can follow these steps:
1. Understanding the Setup:
- We have a square loop of side length L and a small circular loop of radius r (where r<L2) placed at the center of the square loop.
- The plane of the circular loop is perpendicular to the plane of the square loop.
2. Magnetic Field Due to the Square Loop:
- When a current I flows through the square loop, it generates a magnetic field. The magnetic field at the center of the square loop can be calculated, but for our purpose, we need to know that the field is directed out of the plane of the square loop.
3. Area Vector of the Circular Loop:
- The area vector →A of the circular loop is directed perpendicular to its plane. Since the circular loop is perpendicular to the square loop, the area vector points in the same direction as the magnetic field generated by the square loop.
4. Calculating Magnetic Flux:
- The magnetic flux Φ through the circular loop due to the magnetic field B from the square loop can be expressed as:
Φ=B⋅A=B⋅πr2
- Here, A=πr2 is the area of the circular loop.
5. Angle Between Magnetic Field and Area Vector:
- Since the magnetic field B is perpendicular to the area vector A of the circular loop, the angle θ between them is 0∘. Thus, cos(0∘)=1.
6. Mutual Inductance Formula:
- The mutual inductance M is defined as:
M=ΦI
- Since the magnetic field B at the center of the square loop is uniform, the flux through the circular loop can be simplified to:
Φ=B⋅πr2
7. Determining the Magnetic Field B:
- However, the key point here is that the magnetic field B generated by the square loop at the center does not depend on the radius r of the circular loop. For the purpose of mutual inductance, we need to consider the total flux linkage.
8. Conclusion:
- In this specific configuration, due to the geometry and the perpendicular arrangement, the total magnetic flux linked with the circular loop becomes zero. Therefore, the mutual inductance M is:
M=0
Final Answer:
The mutual inductance of the two coils is M=0.
- We have a square loop of side length L and a small circular loop of radius r (where r<L2) placed at the center of the square loop.
- The plane of the circular loop is perpendicular to the plane of the square loop.
- When a current I flows through the square loop, it generates a magnetic field. The magnetic field at the center of the square loop can be calculated, but for our purpose, we need to know that the field is directed out of the plane of the square loop.
- The area vector →A of the circular loop is directed perpendicular to its plane. Since the circular loop is perpendicular to the square loop, the area vector points in the same direction as the magnetic field generated by the square loop.
- The magnetic flux Φ through the circular loop due to the magnetic field B from the square loop can be expressed as:
Φ=B⋅A=B⋅πr2
- Here, A=πr2 is the area of the circular loop.
- Since the magnetic field B is perpendicular to the area vector A of the circular loop, the angle θ between them is 0∘. Thus, cos(0∘)=1.
- The mutual inductance M is defined as:
M=ΦI
- Since the magnetic field B at the center of the square loop is uniform, the flux through the circular loop can be simplified to:
Φ=B⋅πr2
- However, the key point here is that the magnetic field B generated by the square loop at the center does not depend on the radius r of the circular loop. For the purpose of mutual inductance, we need to consider the total flux linkage.
- In this specific configuration, due to the geometry and the perpendicular arrangement, the total magnetic flux linked with the circular loop becomes zero. Therefore, the mutual inductance M is:
M=0
The mutual inductance of the two coils is M=0.
Similar Questions
A circular loop of radius r is placed at the center of current carrying conducting square loop of side a. If both loops are coplanar and a >> r, then the mutual inductance between the loops will be
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View Solution
Knowledge Check
- Question 1 - Select One
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A square loop of sides L is placed at centre of a circular loop of radius r (r << L) such that they are coplanar, then mutual inductance between both loop is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionRadii of two conducting circular loops are b and a respectively, where b>>a Centres of both loops coincide but planes of both loops are perpendicular each other. The value of mutual inductance for these loops
View SolutionA small square loop of n1 turns and side l is placed at the centre of a large coplanar, circular loop of radius r and n2 tuns. The mutual inductacne of the combination is
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are co-planer and their centres coincide. The mutual inductance of the system is proportional to
View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is
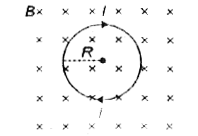 View Solution
View SolutionTwo concentric co - planar circular loops of radius R and r(<<R) are placed as shown in the figure. The mutual inductance of the system will be
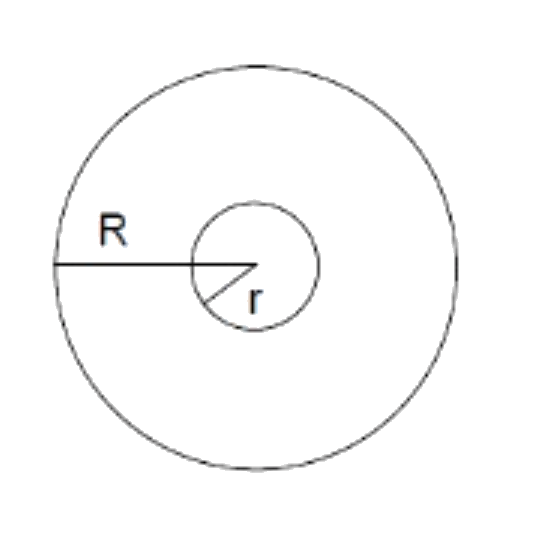 View Solution
View Solution

