The potential difference V across and the current I flowing through an instrument in an AC circuit are given by what will be the avrage power:
V=5cosωt volt
I=2sinωt Amp.
zero
5 watt
10 watt
2.5 watt
The correct Answer is:A
To find the average power in the given AC circuit, we can follow these steps:
Step 1: Identify the Voltage and Current Equations
The voltage V and current I are given as:
V=5cos(ωt)(1)
I=2sin(ωt)(2)
Step 2: Convert Voltage to Sine Form
We can express the cosine function in terms of sine:
V=5cos(ωt)=5sin(ωt+π2)
This shows that the voltage leads the current by 90∘ (or π2 radians).
Step 3: Determine the Phase Difference
From the transformation in Step 2, we can see that the phase difference ϕ between the voltage and current is:
ϕ=90∘
Step 4: Calculate RMS Values
The root mean square (RMS) values for voltage and current are calculated as follows:
Vrms=V0√2=5√2(where V0=5)
Irms=I0√2=2√2(where I0=2)
Step 5: Calculate Average Power
The average power P in an AC circuit is given by the formula:
P=Vrms⋅Irms⋅cos(ϕ)
Substituting the values we have:
- Vrms=5√2
- Irms=2√2
- cos(90∘)=0
Thus, the average power becomes:
P=(5√2)⋅(2√2)⋅0=0
Conclusion
The average power in the circuit is:
0
The voltage V and current I are given as:
V=5cos(ωt)(1)
I=2sin(ωt)(2)
We can express the cosine function in terms of sine:
V=5cos(ωt)=5sin(ωt+π2)
This shows that the voltage leads the current by 90∘ (or π2 radians).
From the transformation in Step 2, we can see that the phase difference ϕ between the voltage and current is:
ϕ=90∘
The root mean square (RMS) values for voltage and current are calculated as follows:
Vrms=V0√2=5√2(where V0=5)
Irms=I0√2=2√2(where I0=2)
The average power P in an AC circuit is given by the formula:
P=Vrms⋅Irms⋅cos(ϕ)
Substituting the values we have:
- Vrms=5√2
- Irms=2√2
- cos(90∘)=0
P=(5√2)⋅(2√2)⋅0=0
The average power in the circuit is:
0
Topper's Solved these Questions
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -2 Part-1
Explore 14 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -2 Part-2
Explore 6 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:HIGH LEVEL PROBLEMS
Explore 11 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
Similar Questions
The potential difference V across and the current I flowing through an instrument in an AC circuit are given by:
V=5cosωt volt
I=2sinωt Amp.
View SolutionThe potential differences V and the current i flowing through an instrument in an AC circuit of frequency f are given by V=5cosωt and I=2sinωt amperes (where ω=2πf). The power dissipated in the instrument is
View SolutionIn the given circuit current flowing through 2 Omega resistance is
View SolutionThe potential difference E and current I flowing through the ac circuit is given by E=5cos(ωt−π/6)VandI=10sin(ω)tA. Find the average power dissipated in the circuit.
View SolutionThe current I1 (in A) flowing through the 1Ω resistor in the given circuit is
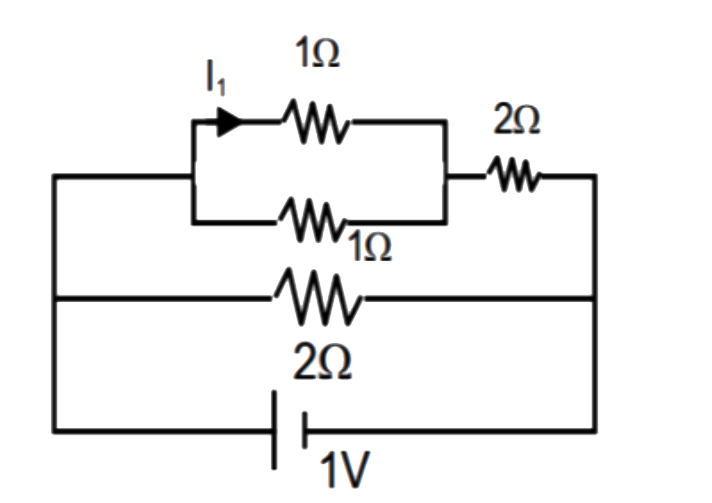
View SolutionThe current I1 ( in A ) flowing through 1 Ω resistor in the following circuit is :
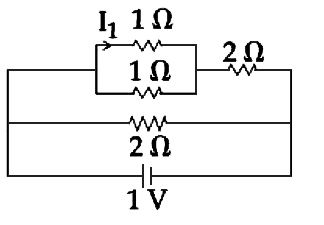
View SolutionThe current I1 (in A) flowing through 3Ω resistor in the following circuit is:
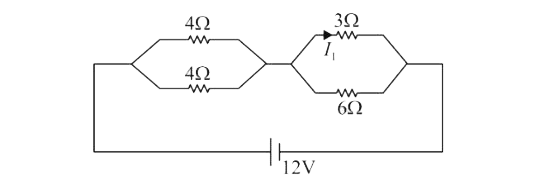
View SolutionCurrent in an ac circuit is given by I=3sinωt+4cosωt, then
View SolutionThe voltage and current in a series AC circuit are given by V=V0cosωtandI=i0sinωt.
What is the power dissipated in the circuit?
View SolutionCalculate the current flowing through a wire of resistance 5 Ω connected to a battery of potential difference 3 V.
View Solution
