The average value of a saw-tooth voltage V=V0(2tT−1) Over 0 to T2, (T- time period) is given by
V0√2
2V0π
V02
V0
The correct Answer is:C
To find the average value of the saw-tooth voltage V=V0(2tT−1) over the interval from 0 to T2, we can follow these steps:
1. Define the Average Value Formula:
The average value Vavg of a function V(t) over an interval (a,b) is given by:
Vavg=1b−a∫baV(t)dt
Here, a=0 and b=T2.
2. Set Up the Integral:
Substitute V(t) into the average value formula:
Vavg=1T2−0∫T20V0(2tT−1)dt
This simplifies to:
Vavg=2T∫T20V0(2tT−1)dt
3. Integrate the Function:
Now, we need to calculate the integral:
∫T20(2V0tT−V0)dt
This can be split into two separate integrals:
=∫T202V0tTdt−∫T20V0dt
4. Calculate Each Integral:
- For the first integral:
∫T202V0tTdt=2V0T⋅t22∣∣∣T20=2V0T⋅(T2)22=2V0T⋅T28=V0T4
- For the second integral:
∫T20V0dt=V0⋅t∣∣∣T20=V0⋅T2
5. Combine the Results:
Now substituting back into the average value formula:
Vavg=2T(V0T4−V0⋅T2)
Simplifying this gives:
Vavg=2T(V0T4−V0T2)=2T(V0T4−2V0T4)=2T(−V0T4)=−V02
6. Final Result:
Thus, the average value of the saw-tooth voltage over the interval (0,T2) is:
Vavg=V02
The average value Vavg of a function V(t) over an interval (a,b) is given by:
Vavg=1b−a∫baV(t)dt
Here, a=0 and b=T2.
Substitute V(t) into the average value formula:
Vavg=1T2−0∫T20V0(2tT−1)dt
This simplifies to:
Vavg=2T∫T20V0(2tT−1)dt
Now, we need to calculate the integral:
∫T20(2V0tT−V0)dt
This can be split into two separate integrals:
=∫T202V0tTdt−∫T20V0dt
- For the first integral:
∫T202V0tTdt=2V0T⋅t22∣∣∣T20=2V0T⋅(T2)22=2V0T⋅T28=V0T4
- For the second integral:
∫T20V0dt=V0⋅t∣∣∣T20=V0⋅T2
Now substituting back into the average value formula:
Vavg=2T(V0T4−V0⋅T2)
Simplifying this gives:
Vavg=2T(V0T4−V0T2)=2T(V0T4−2V0T4)=2T(−V0T4)=−V02
Thus, the average value of the saw-tooth voltage over the interval (0,T2) is:
Vavg=V02
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - C ) (Objective Type Questions) ( More than one option are correct)
2 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - D) (Linked Comprehension Type Questions)
3 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - A) ( Objective Type Questions ( One option is correct))
40 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )
5 Videos
Similar Questions
The average value of an alternating voltage V=V0sinωt over a full cycle is
View SolutionThe average value of an alternating voltage V=V0sinωt over a full cycle is
View SolutionThe average value of current for the current shown for time period 0 to T2 is

View SolutionThe rms value of the saw-tooth voltage of peak value V0 from t=0 to t=2T as shown in figure is V0√x.Find the value of x.
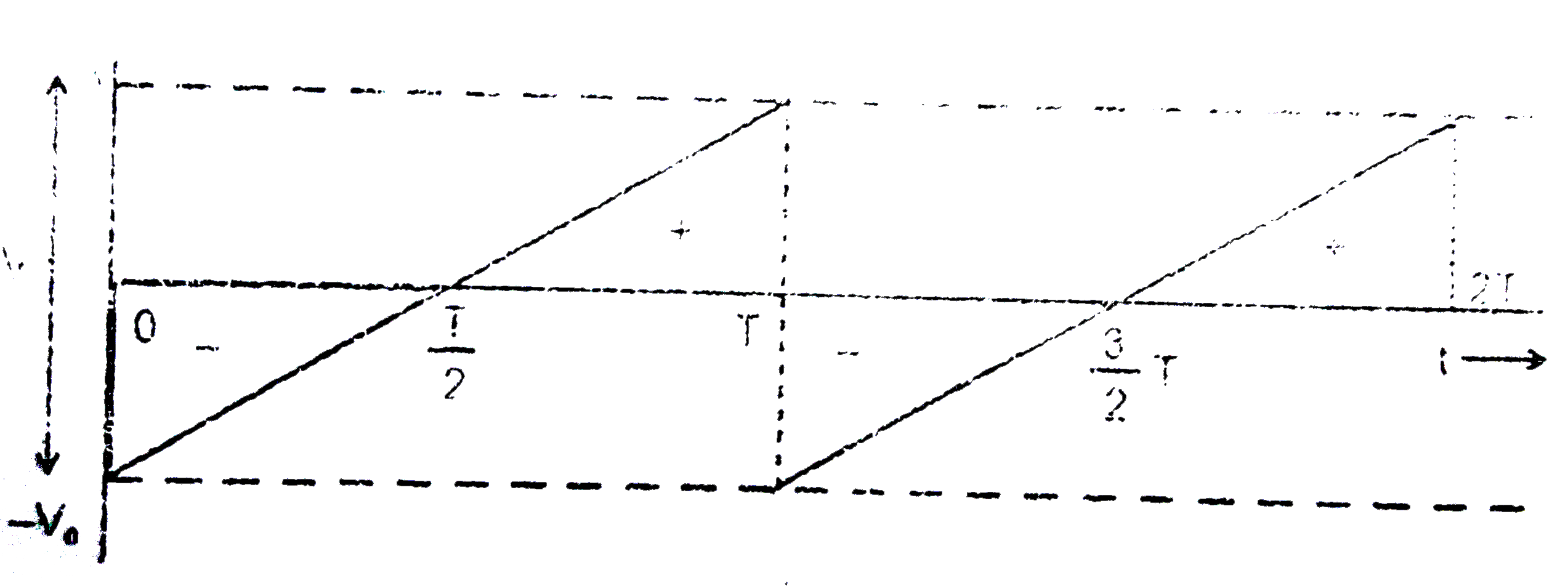
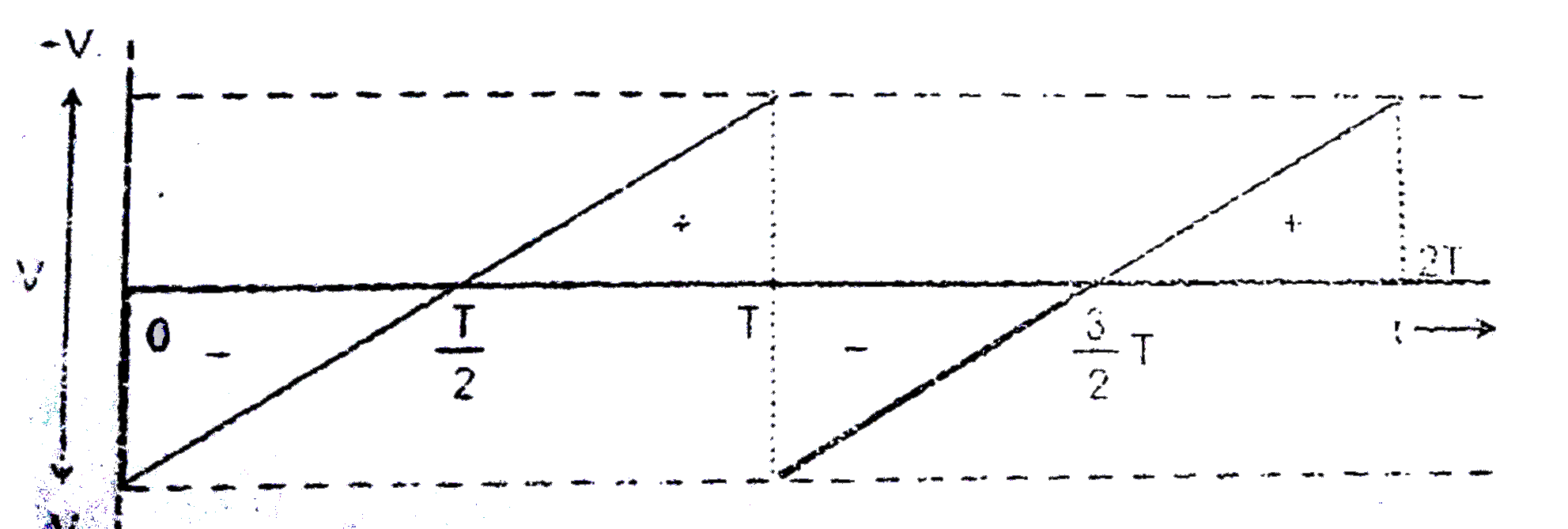
View SolutionFind the aveage for the saw-tooth voltage of peak value V0 from t=0 to t=2T as shown in figure.
View SolutionThe voltage supplied to a circuit is given by V=V0t32, where t is time in second. Find the rms value of voltage for the period, t=0 to t=1s.
View SolutionFind the average speed of a particle whose velocity is given by V=V0sinωt t where T=2π/ω is the time of complete cycle
View SolutionIf V=220√2sin(314t−ϕ) calculat peak and rms value of the voltage (b) average voltage for half time -period (c ) frequency of ac
View SolutionA particle is moving in a circle of radius 4cm with constant speed of 1cm/s. Find
(a) time period of the particle.
(b) average speed, average velocity and average acceleration in a time interval from t=0 to t=T4. Here, T is the time period of the particle. Give only their magnitudes.
View SolutionFind the value of ln(∫10et2+t(2t2+t+1)dt)
View Solution
