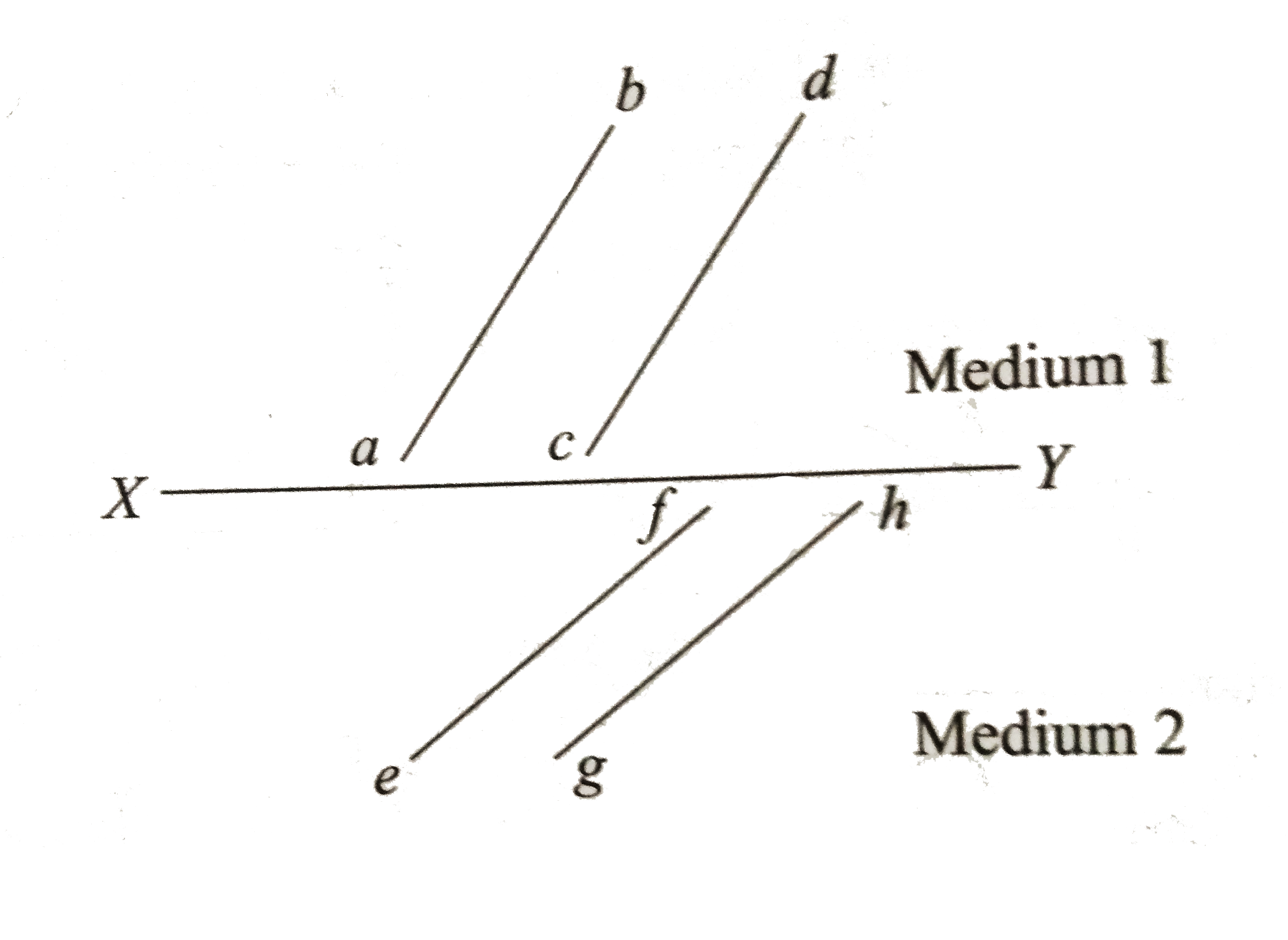
Fig. shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave travelling in medium 1 and incident on XY. Line ef and gh represent wavefront of the light wave in medium 2 after rafraciton. Speed of light is
$Fig. shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave travelling in medium 1 and incident on XY. Line ef and gh represent wavefront of the light wave in medium 2 after rafraciton. Speed of light is$

A

$ϕ_{c}$ cannot be equal to $ϕ_{d}$

B

$ϕ_{d}$ cannot be equal to $ϕ_{e}$

C

$(ϕ_{d} - ϕ_{f})$ is equal to $(ϕ_{c} - ϕ_{e})$

D

$(ϕ_{d} - ϕ_{c})$ is equal to $(ϕ_{f} - ϕ_{e})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$c$ and $d$ are at same wavefronts
So, $ϕ_{c} = ϕ_{d}$
and $ϕ_{e} = ϕ_{f}$
$∴ ϕ_{d} - ϕ_{f} = ϕ_{c} - ϕ_{f}$
$D$ is incorrect
$ϕ_{d} - ϕ_{c} = 0$
$ϕ_{f} - ϕ_{e} = 0$
So both should be equal.

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider two adjacent transparent media. The speed of light in medium 1 is $v_{1}$ , and the speed of light in medium 2 is $v_{2}$ . If $v_{1} < v_{2}$ , then total internal reflection will occur at the interface between these media if a beam of light is
Aincident in medium 1 and strikes the interface at an angle of incidence greater than ${sin}^{- 1} (v_{1} / v_{2})$ .
Bincident in medium 1 and strikes the interface at an angle of incidence greater than ${sin}^{- 1} (v_{2} / v_{1})$ .
Cincident in medium 2 and strikes the interface at an angle of incidence greater than ${sin}^{- 1} (v_{1} / v_{2})$ .
Dincident in medium 2 and strikes the interface at an angle of incidence greater than ${sin}^{- 1} (v_{2} / v_{1})$ .

RESONANCE ENGLISH-WAVE OPTICS-Exercise-3 (Part-1)

Home
Ask Doubt
Profile