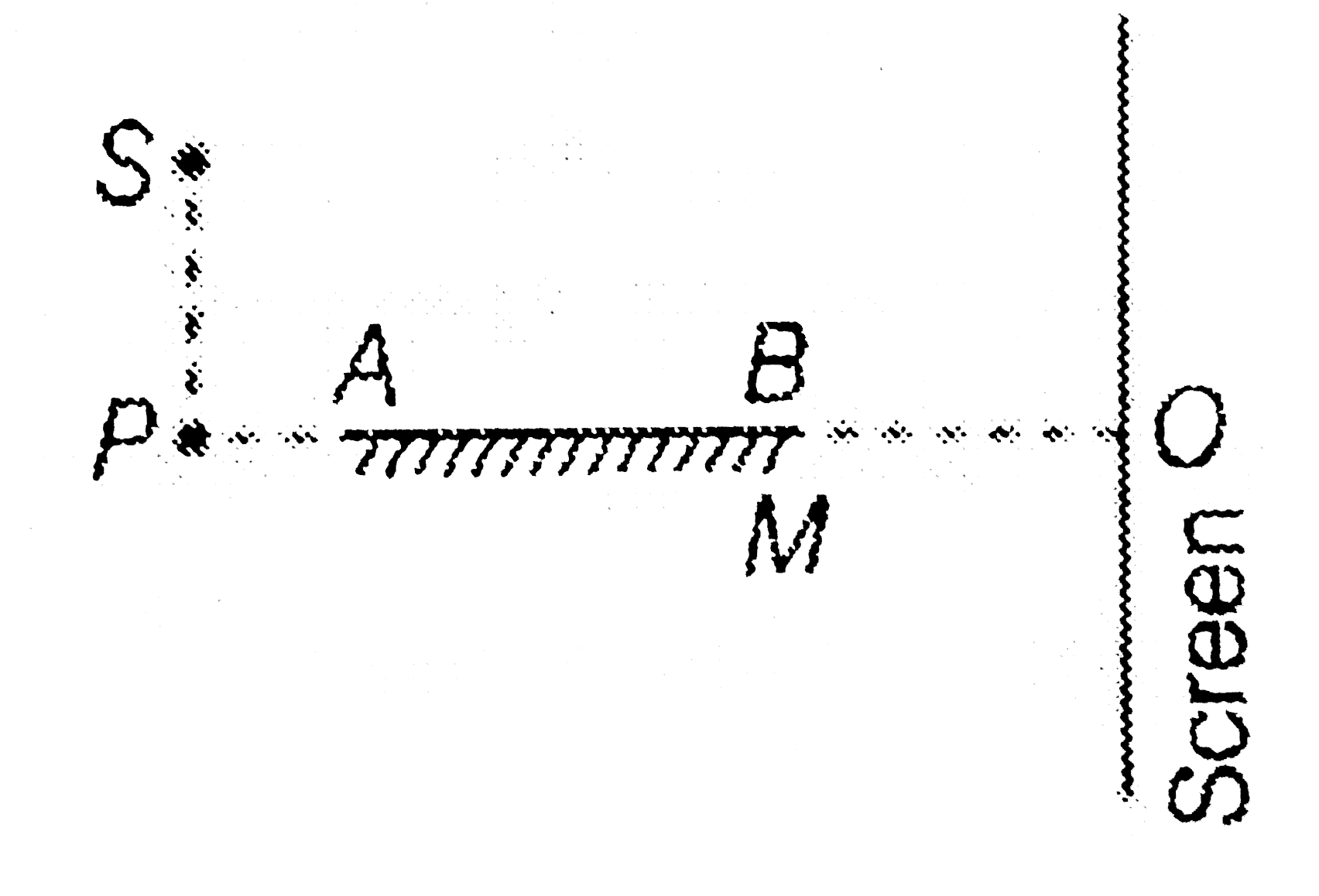
Two identical narrow slits S1 and S2 are illuminated by light of wavelength λ from a point source P. If, as shown in the diagram above the light is then allowed to fall on a scree, and if n is a positive integer, the condition for destructive interference at Q is that

The correct Answer is:3
For constructive interference Δx=mλ
43√d2+x2−√d2+x2=mλ
12√d2+x2=mλ
x2=9m2λ2−d2
p=3

Topper's Solved these Questions
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise-3 (Part-2)
15 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise-3 (Part-3)
22 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise-2 (Part-4)
8 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 3 PART II
7 Videos
Similar Questions
Two identical narrow slits S1andS2 are illuminated by the light of a wavelengthλ from a point source P.
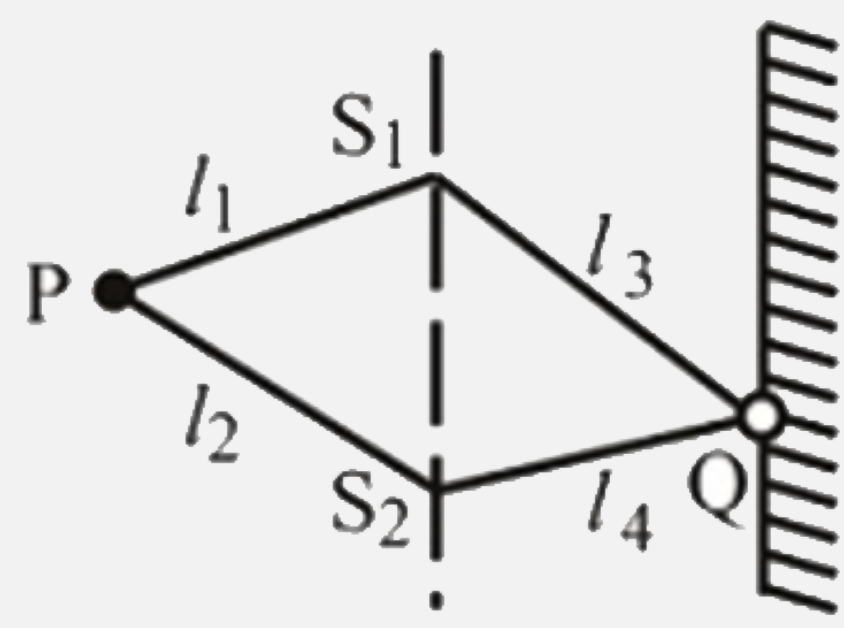
If , as shown in the diagram above , the light is then allowed to fall on a screen , and if n is a positive integer , the condition for destructive interference at Q is
View SolutionTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
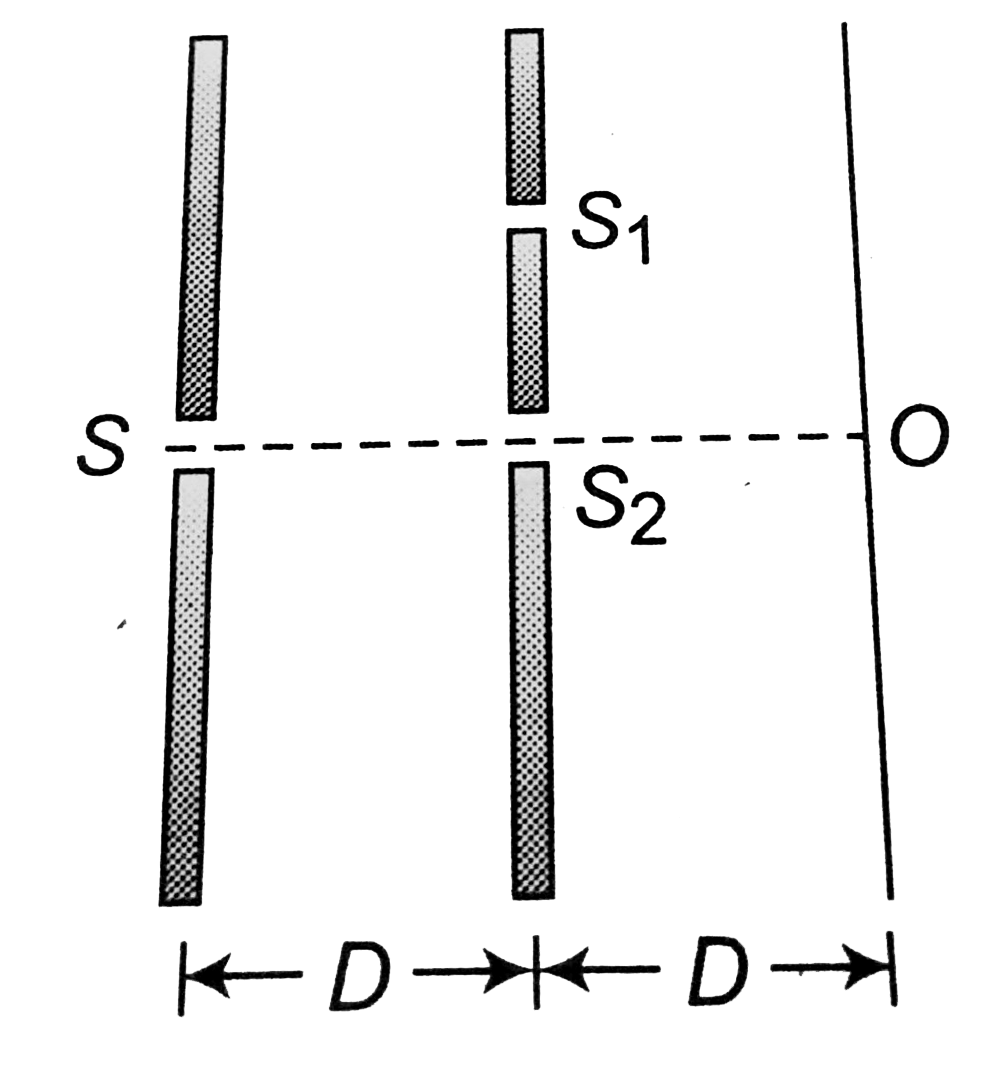
View SolutionTwo ideal slits S1 and S2 are at a distance d apart, and illuninated by light of wavelength λ passing through an ideal source slit S placed on the line through S2 as shown. The distance between the planes of slits and the source slit is D.A screen is held at a distance D from the plane of the slits. The minimum value of d for which there is darkness at O is (d<<D)
View SolutionLight of wavelength λ from a point source falls on a small circular rings around a central bright spot are formed on a screen beyond the obstacle The distance between the screen and obstacle is D. Then, the condition for the formation of rings, is
View SolutionConsider the situation shown in figure. The two slite S1andS2
placed symmetrically around the centre line are illuminated by a monochromatic
light of wavelength lambda. The separation between the slits is d. The light transmitted
by the slits falls on a screen M1 placed at a distance D from the slits. The slit S3 is
at the centre line and the slit S4 is at a distance y form S3. Another screen M2 is
placed at a further distance D away from M1. Find the ration of the maximum to
minimum intensity observed on M2 if y is equal to (d<<D).
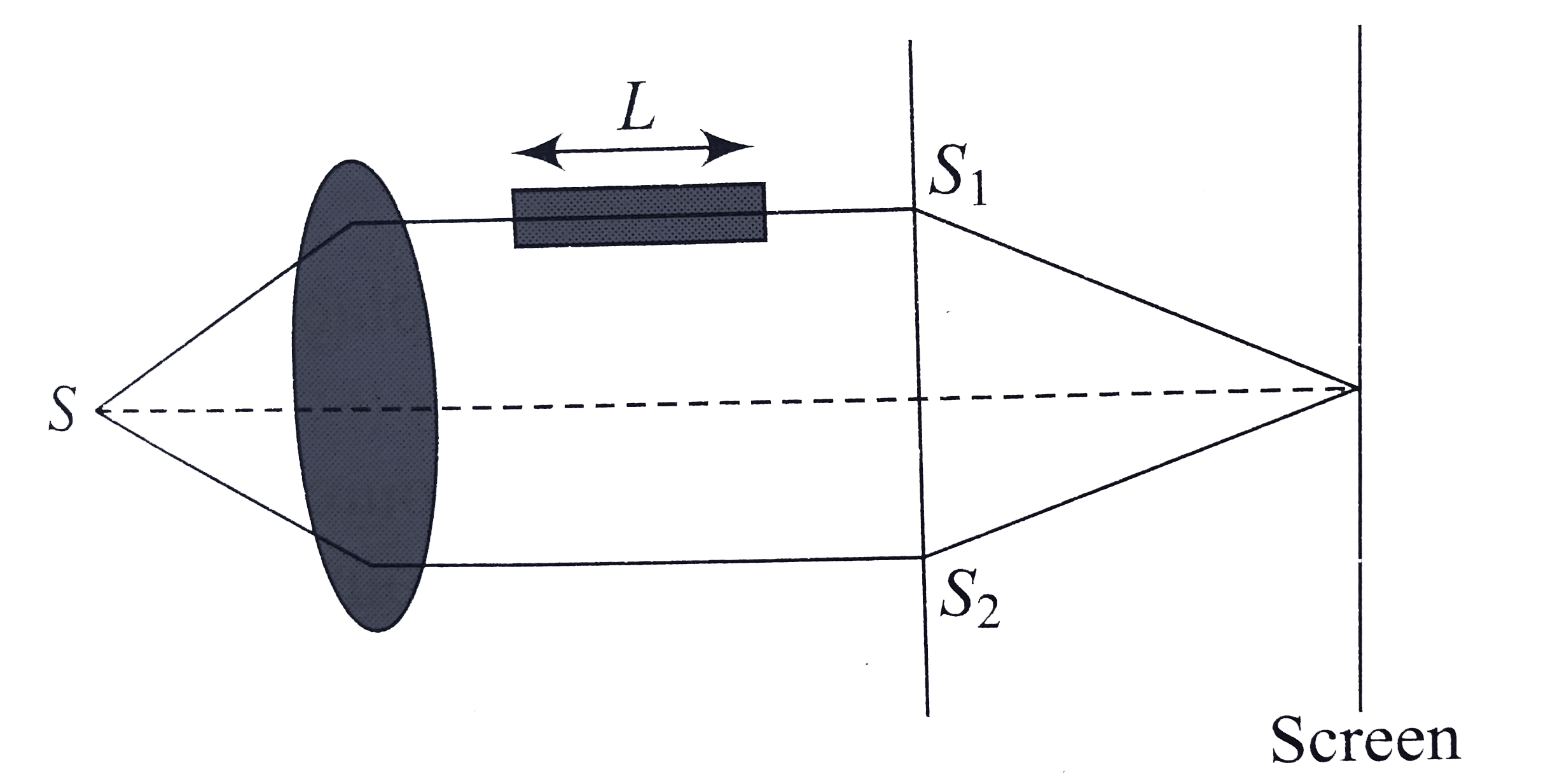
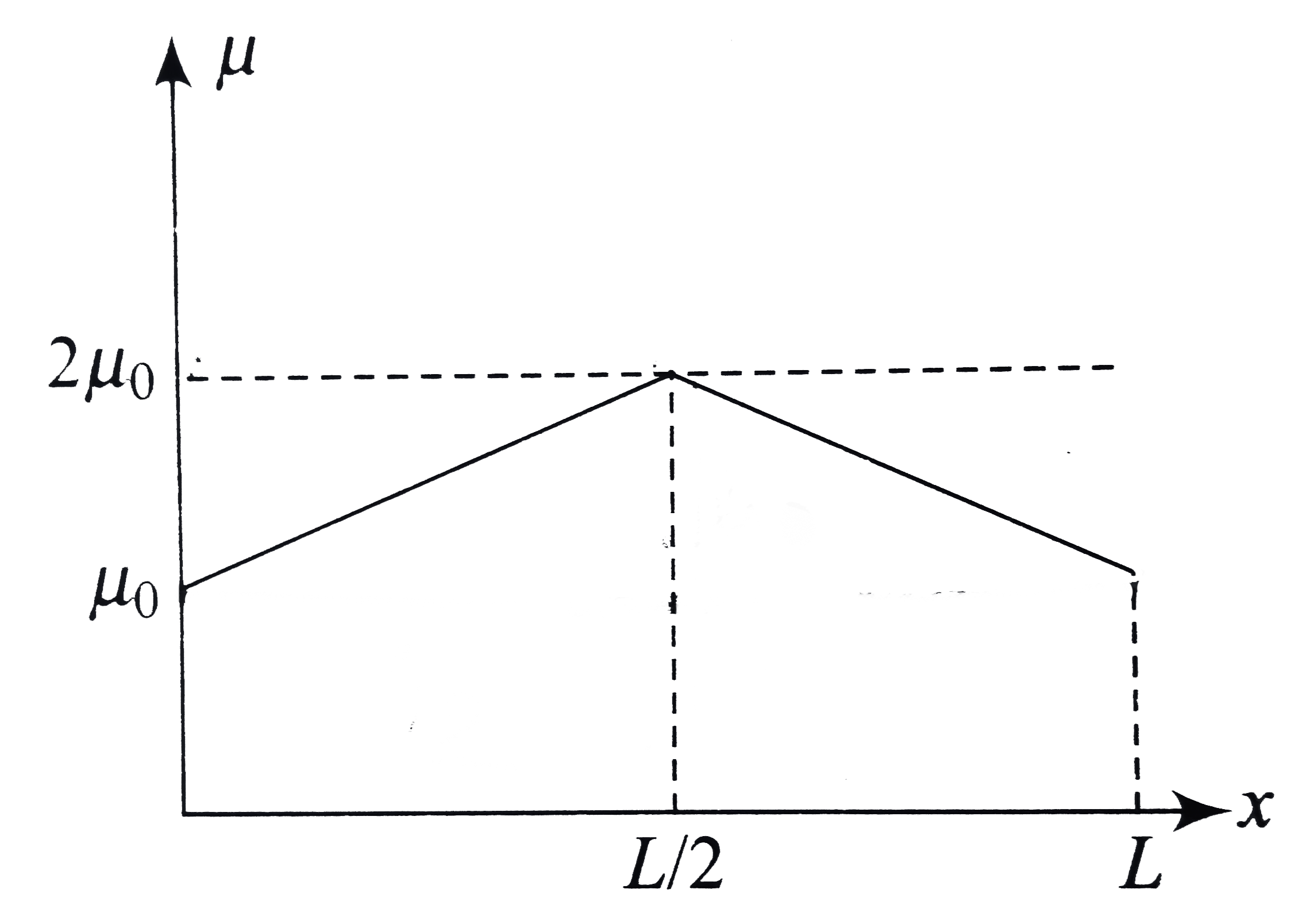
View SolutionFigure shows a narrow slit S illuminated b a monochromatic light of wavelength λ in a double-slit experiment. In the path of the rays reaching the upper slit S1, a tube to length L is interposed in which the index of reflection of the medium varies linearly as shown in figure . The position of the central maximum in the interference pattern on the screen was displaceed by N fringes. Find the value of N in terms of μ0, L and λ.
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View SolutionFollowing figures shows sources S1 and S2 that emits light of wavelength λ in all directions. The sources are exactly in phase and are separated by a distance equal to 1.5λ. If we start at the indicated start point and travel along path 1 and 2, the interference produce a maxima all along

View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View SolutionIn a Lloyds's mirror experiment as narrow slit S transmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?
View Solution
