A particle undergoes S.H.M. having time period T . The time taken in 3 /8th oscillation is
3 T /8
5 T / 8
5 T /12
7 T /12
The correct Answer is:(a)1211V (b)(b)−8V
To solve the problem of finding the time taken for a particle undergoing Simple Harmonic Motion (S.H.M.) to complete 38 of its oscillation with a time period T, we can follow these steps:
1. Understanding the Oscillation:
- In one complete oscillation, the particle moves from the mean position (O) to the maximum displacement (A), back to the mean position (O), then to the opposite maximum displacement (B), and finally returns to the mean position (O). This constitutes a full cycle.
2. Dividing the Oscillation:
- A complete oscillation can be divided into 4 equal parts:
- From O to A (1/4 of the oscillation)
- From A to O (1/4 of the oscillation)
- From O to B (1/4 of the oscillation)
- From B to O (1/4 of the oscillation)
3. Calculating Time for Each Segment:
- The time taken for one complete oscillation is T.
- Therefore, the time taken for 14 of the oscillation is:
Time for 14 oscillation=T4
4. Finding Time for 38 of the Oscillation:
- We can express 38 of the oscillation as:
38=28+18=14+18
- The time taken for 14 of the oscillation is T4.
- Now, we need to find the time taken for 18 of the oscillation:
Time for 18 oscillation=T8
5. Adding the Times:
- The total time taken for 38 of the oscillation is:
Total time=Time for 14+Time for 18=T4+T8
6. Finding a Common Denominator:
- To add T4 and T8, we find a common denominator:
T4=2T8
- Now we can add:
2T8+T8=3T8
7. Final Calculation:
- The total time taken for 38 of the oscillation is:
Total time=3T8
Conclusion:
The time taken in 38 of the oscillation is 5T12.
- In one complete oscillation, the particle moves from the mean position (O) to the maximum displacement (A), back to the mean position (O), then to the opposite maximum displacement (B), and finally returns to the mean position (O). This constitutes a full cycle.
- A complete oscillation can be divided into 4 equal parts:
- From O to A (1/4 of the oscillation)
- From A to O (1/4 of the oscillation)
- From O to B (1/4 of the oscillation)
- From B to O (1/4 of the oscillation)
- The time taken for one complete oscillation is T.
- Therefore, the time taken for 14 of the oscillation is:
Time for 14 oscillation=T4
- We can express 38 of the oscillation as:
38=28+18=14+18
- The time taken for 14 of the oscillation is T4.
- Now, we need to find the time taken for 18 of the oscillation:
Time for 18 oscillation=T8
- The total time taken for 38 of the oscillation is:
Total time=Time for 14+Time for 18=T4+T8
- To add T4 and T8, we find a common denominator:
T4=2T8
- Now we can add:
2T8+T8=3T8
- The total time taken for 38 of the oscillation is:
Total time=3T8
The time taken in 38 of the oscillation is 5T12.
Topper's Solved these Questions
Similar Questions
A paricle performs S.H.M. with time period T. The time taken by the particle to move from hall the amplitude to the maximum dispalcement is T2
View SolutionA particle executes S.H.M with time period 12 s. The time taken by the particle to go directly from its mean position to half its amplitude.
View Solution
Knowledge Check
A particle executing SHM with time period T and amplitude A. The mean velocity of the particle averaged over quarter oscillation, is
AA4TB2ATC3ATD4AT
A particle executes SHM with a time period of 4s. Find the time taken by the particle to go directly from its mean position to half of its amplitude.
View SolutionA particle executes SHM with a time period of 4 s . Find the time taken by the particle to go from its mean position to half of its amplitude . Assume motion of particle to start from mean position.
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
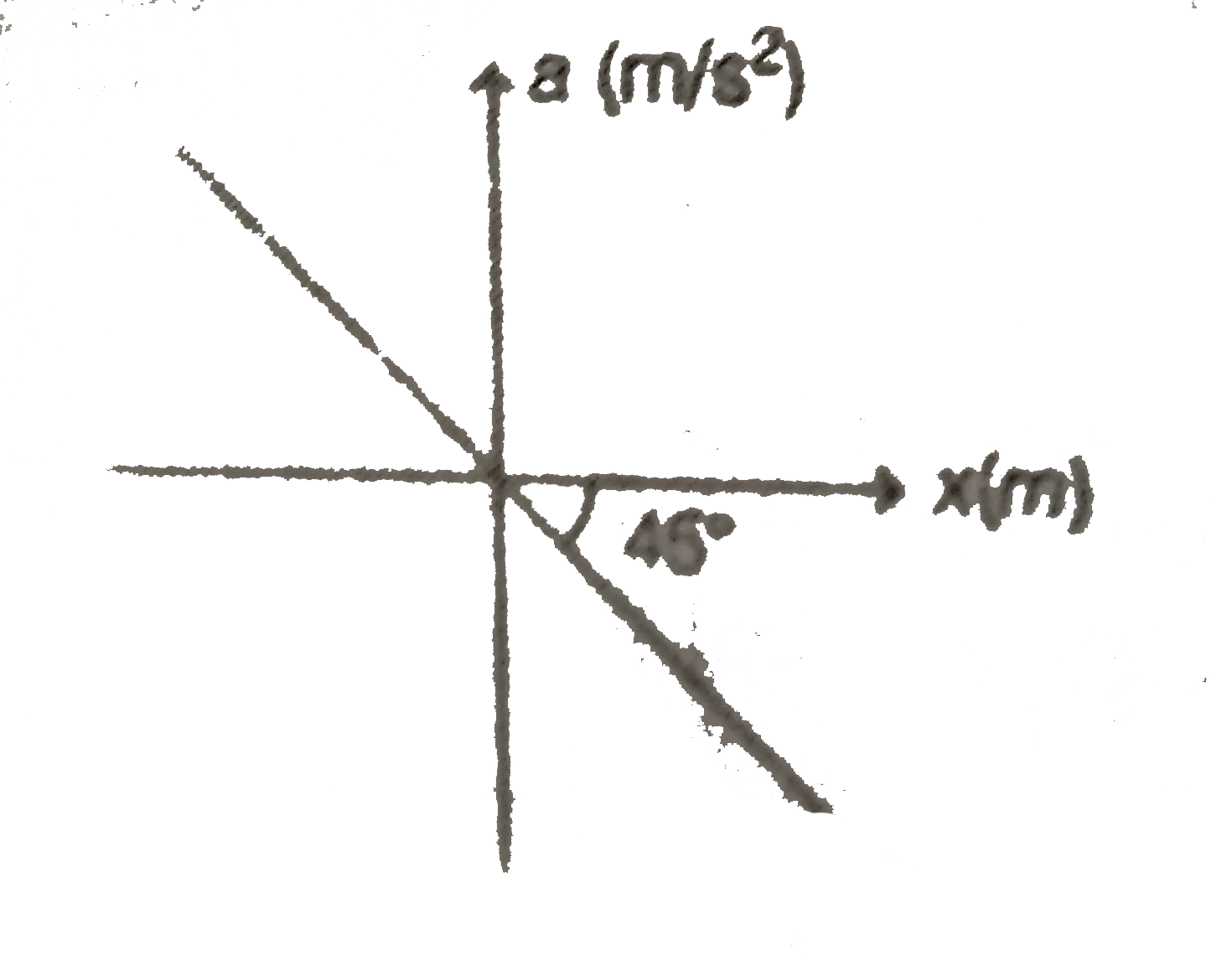
View SolutionThe time period of small oscillations of mass m :-
_S01_040_Q01.png)
View SolutionA particle executing SHM with time period of 2s: Find the time taken by it to move from one amplitude to half the amplitude position.
View SolutionAcceleration displacement (a-x) graph of a particle executing S.H.M. is shown in the figure. The frequency of oscillation is (tanθ=8)
View SolutionA particle executes linear SHM with time period of 12 second. Minimum time taken by it to travel from positive extreme to half of the amplitude is
View Solution