A conductor of length l has a non-uniform cross-section. The radius of cross-section varies linearly from a to b. The resistivity of the material is ρ. Find the resistance of the conductc across its ends.

In this problem cross-section area is variable so we can't apply formula (R=ρlA) directly.
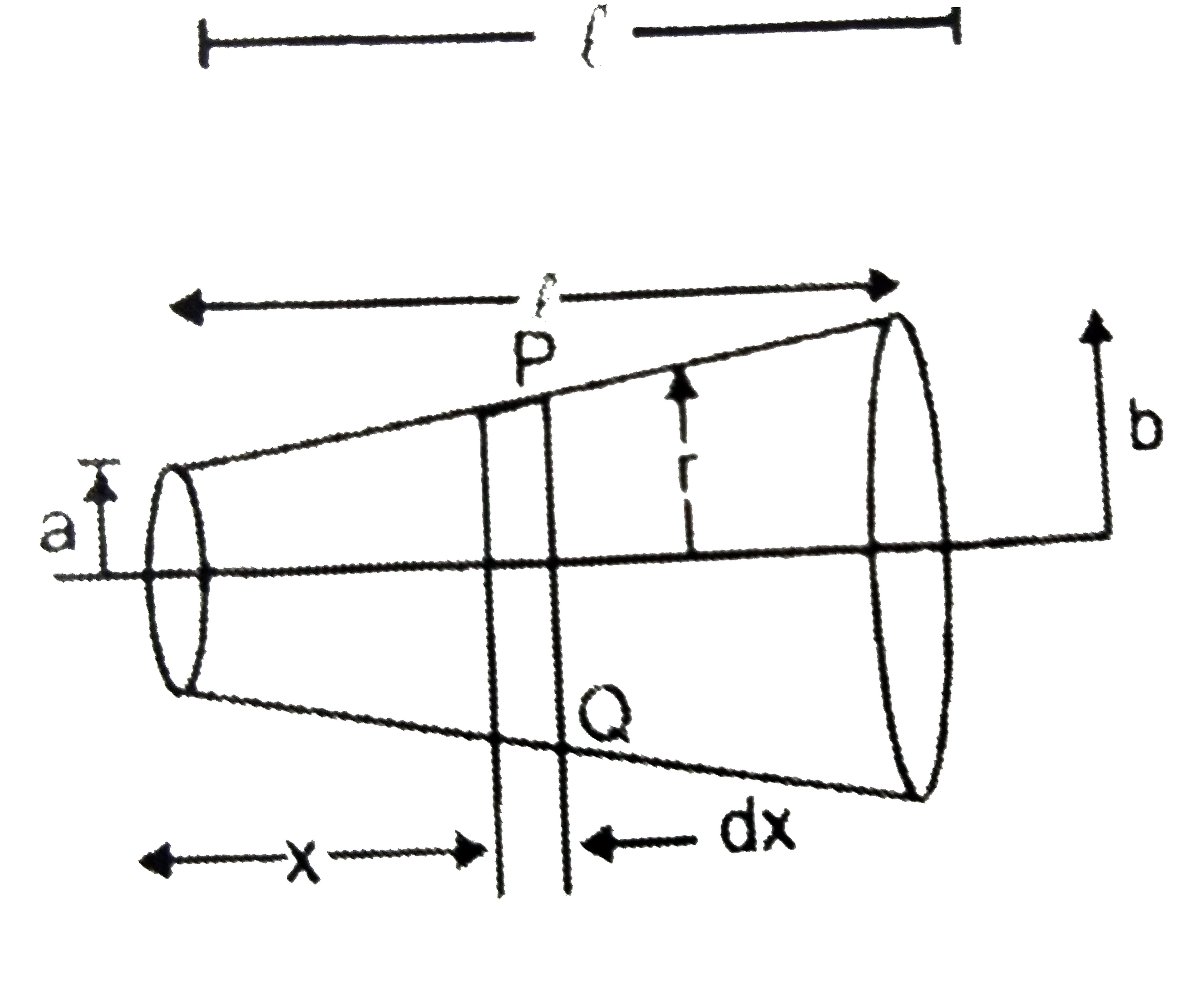
So we assume elementary strip 'PQ' of thickness dx and radius r resistance of this strip is :
dR=ρdxπr2
Bt grometry r−ax=b−at⇒r=b−alx+a
Resistance of conductor is R=t∫0pdxπ{b−alx+a}⇒R=ρlπab
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-1)41videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-2)47videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 313videos
COMMUNICATION SYSTEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.711videos
DAILY PRACTICE PROBLEM
Similar Questions
Shown a conductor of length l having a circular cross section. The radius of cross section varies linearly form a→b. The resistivity of the material is(ρ).Assuming that b−a<<l,find the resistance of the conductor.
 View Solution
View SolutionIf the radius of cross-section of the conductor is increased by 0.1% keeping volume constant, then percentage change in the resistance of the conductor is
View SolutionA rod of length L is of non uniform cross-section. Its mass per unit length varies linearly with distance from left end. Then its centre of mass from left end is at a distance. (Take linear density at left end=0).
 View Solution
View SolutionA cylindrical conductor of length l and uniform area of cross-section A has resistance R. Another conductor of length 2l and resistance R of the same material has area of cross-section :
View SolutionResistivity of a conductor of length l and cross - section A is ρ . If its length is doubled and area of cross-section is halved, then its new resistivity will be .
View SolutionA cylinder conductor AB of non uniform area of cross-section carries a current of 5A. The radius of the conductor at one end A is 0.5 cm.The current density at the other end of the conductor is half of the value at A. The radius of the conductor at the end B is nearly
View SolutionThe ends of a long bar are maintained at different temperatures and there is no loss of heat from the sides of the bar due to conduction or radiation. The graph of temperature against distance of the bar when it has attained steady state is shown here. The graph shows (i) the temperature gradient is not uniform.
(ii) the bar has uniform cross-sectional area.
(iii) the cross-sectional area of the bar increases as the distance from the hot end increases.
(iv) the cross-sectional area of the bar becreases as the distance from the hot end increasesView SolutionA cylindrical conductor has uniform cross-section. Resistivity of its material increase linearly from left end to right end. If a constant current is flowing through it and at a section distance x from left end, magnitude of electric field intensity is E , which of the following graphs is correct
View SolutionA cylindrical conductor has uniform cross-section. Resistivity of its material increase linearly from left end to right end. If a constant current is flowing through it and at a section distance x from left end, magnitude of electric field intensity is E , which of the following graphs is correct
View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View Solution

