A thin wire of length L and cross-sectional area A oriented in the x-direction is made up of an ohmic material whose resistivity varies along the wire according to the empirical law ρ=ρ0e−x/lL
(i) Determine how the field with in wire varies with position if the end at x=0 is at potential V0 greater than the end at x=L.
(ii) How does potential varies as you move along the wire ?
(Iii) What is resistance of the wire ?
The correct Answer is:(a)R=ρ0LA(e−1e),i=V0R,
(b)V(X)=Vo(e−X/L)1−e−1
Step by step video & image solution for A thin wire of length L and cross-sectional area A oriented in the x-direction is made up of an ohmic material whose resistivity varies along the wire according to the empirical law rho = rho_(0)e^(- x //lL) (i) Determine how the field with in wire varies with position if the end at x=0 is at potential V_(0) greater than the end at x=L. (ii) How does potential varies as you move along the wire ? (Iii) What is resistance of the wire ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exrcies-3(PART-2)
23 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
Similar Questions
A rod of length L and cross-section area A lies along the x-axis between x=0 and x=L. The material obeys Ohm's law and its resistivity varies along the rod according to ρ(x)=ρ0ε−x/L. The end of the rod x=0 is at a potential V0 and it is zero at x=L.
(a) Find the total resistance of the rod and the current in the wire.
(b) Find the electric potential in the rod as a function of x.
View SolutionThe V – I graph for a wire of copper of length L and cross -section area A is shown in the figure below . The slope of the graph will be
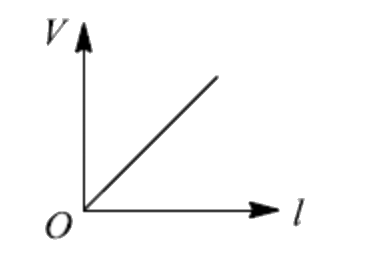
View Solution
Knowledge Check
A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2LA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAl
The V – I graph for a wire of copper of length L and cross -section area A is shown in the figure below . The slope of the graph will be

View SolutionA current i passes through a wire of length l , radius of cross-section r and resistivity ρ . The rate of heat generation is
View SolutionThere are three copper wires of length and cross-sectional area (L,A),(2L,A/2)(L/2,2A). In which case in the resistance minimum?
View SolutionA wire of length l and cross-sectional are A is suspended at one of its ends from a ceiling. What will be its strain energy due to its own weight, if the density and Young's modulus of the material of the wire be d and Y?
View SolutionI−V characterstic of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
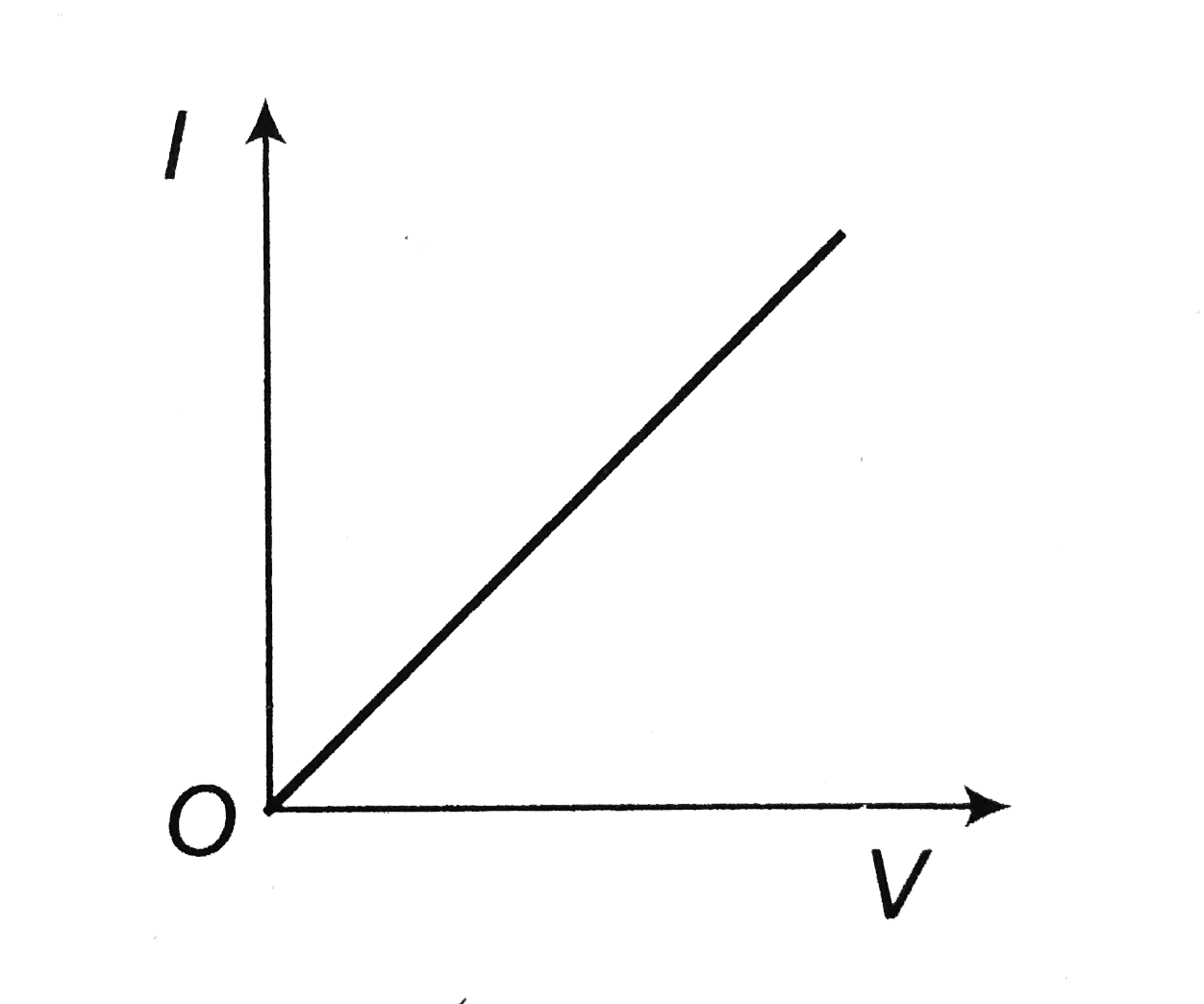
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View Solution
