A nichrome wire uniform cross-sectional area is bent to form a rectangular loop ABCD. Another nichrome wire of the same cross-section is connected to form the diagonal AC. Find out the ratio of the resistances across BD and AC if AB = 0.4 m and BC = 0.3 m.
The correct Answer is:RBDRAC=5935
To find the ratio of the resistances across BD and AC in the given rectangular loop ABCD with a diagonal AC, we will follow these steps:
Step 1: Determine the lengths of the sides of the rectangle
Given:
- Length AB = 0.4 m
- Length BC = 0.3 m
Using the Pythagorean theorem, we can find the length of the diagonal AC:
AC=√AB2+BC2=√(0.4)2+(0.3)2=√0.16+0.09=√0.25=0.5m
Step 2: Calculate the resistances of each segment
The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area. Since both wires are made of nichrome and have the same cross-sectional area, the resistance is directly proportional to the length.
- Resistance of AB:
RAB=k×0.4m(k is a constant depending on ρ and A)
- Resistance of BC:
RBC=k×0.3m
- Resistance of AC:
RAC=k×0.5m
Step 3: Calculate the equivalent resistance across AC
The total resistance across AC can be calculated as:
RAC=RAB+RBC=k×0.4+k×0.3=k×(0.4+0.3)=k×0.7
Step 4: Calculate the equivalent resistance across BD
For the path BD, we have:
- Resistance from B to A (AB): RAB=k×0.4
- Resistance from A to D (AD): RAD=k×0.3
- Resistance across AC: RAC=k×0.5
The resistances in series for BD are:
RBD=RAB+RAD+RAC=k×0.4+k×0.3+k×0.5=k×(0.4+0.3+0.5)=k×1.2
Step 5: Find the ratio of resistances RBD to RAC
Now, we can find the ratio of the resistances:
Ratio=RBDRAC=k×1.2k×0.7=1.20.7=127
Final Result
Thus, the ratio of the resistances across BD and AC is:
RBDRAC=127
Given:
- Length AB = 0.4 m
- Length BC = 0.3 m
AC=√AB2+BC2=√(0.4)2+(0.3)2=√0.16+0.09=√0.25=0.5m
The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area. Since both wires are made of nichrome and have the same cross-sectional area, the resistance is directly proportional to the length.
RAB=k×0.4m(k is a constant depending on ρ and A)
RBC=k×0.3m
RAC=k×0.5m
The total resistance across AC can be calculated as:
RAC=RAB+RBC=k×0.4+k×0.3=k×(0.4+0.3)=k×0.7
For the path BD, we have:
- Resistance from B to A (AB): RAB=k×0.4
- Resistance from A to D (AD): RAD=k×0.3
- Resistance across AC: RAC=k×0.5
RBD=RAB+RAD+RAC=k×0.4+k×0.3+k×0.5=k×(0.4+0.3+0.5)=k×1.2
Now, we can find the ratio of the resistances:
Ratio=RBDRAC=k×1.2k×0.7=1.20.7=127
Thus, the ratio of the resistances across BD and AC is:
RBDRAC=127
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exrcies-3(PART-2)
23 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
Similar Questions
One end of a Nichrome wire of length 2L and cross-sectional area A is attached to an end of another Nichrome wire of length L and cross-sectional area 2A. If the free end of the longer wire is at an electric potential of 8.0 volts, and the free end of the shorter wire is at an electric potential 1.0 volts, the potential at the junction of the two wires is equal to
View SolutionFour cells each of emf E and internal resistance r are connected in series to form a loop ABCD. Find potential difference across (1) AB, (2) AC
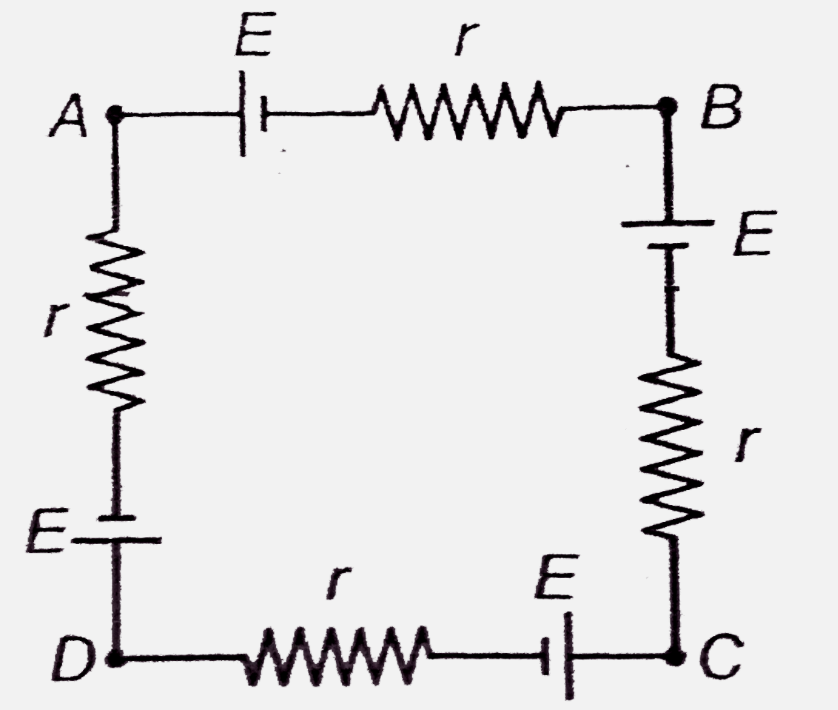
View Solution
Knowledge Check
A metal wire of length L1 and area of cross section A is attached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
A[(Y1Y2)A][2(Y1L2+Y2L1)]B[(Y1Y2)A](L1L2)2C[(Y1Y2)A](Y1L2+Y2L1)D[(Y1Y2)1/2A](L2+L1)1/2A metal wire of length L1 and area of cross section A is ttached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
AY1Y2A2(Y1L2+Y2L1)BY1Y2A(L1L2)1/2CY1Y2A(Y1L2+Y2L1)D(Y1Y2)1/2A(L1L2)1/2
A steel wire when bent in the form of a square encloses an area of 121 cm2 . If the same wire is bent in the form of a circle, find the area of the circle.
View SolutionA steel wire when bent in the form of a square encloses an area of 121 cm2 . If the same wire is bent in the form of a circle, find the area of the circle.
View SolutionA wire of resistance 0.1 cm−1 bent to form a square ABCD of side 10 cm. A simailar wire is connected between the corners B and D to form the diagonal BD. Find the effective resistance of this combination between cornaers A and C. If a 2V battery of negligible internal resistance is connected across A and C calculate the total power dissipated.
View SolutionTwo wires of the same materical having equal area of cross-section have L and 2L. Their respective resistances are in the ratio
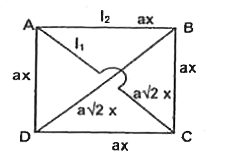
View SolutionABCD is a square of side 'a' metres and is made of wires of resistance x ohms//metre. Similar wires are connected across the diagonals AC and BD. The effective resistance between the ax corners A and C will be
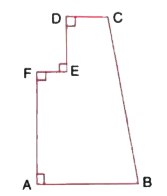
View SolutionThe figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 m, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
View Solution
