Two point charges 2μC and −2μC are placed at point A and B as shown in figure. Find out electric field intensity at points C and D. [All the distances are measured in meter].
![Two point charges 2 muC and -2 muC are placed at point A and B as shown in figure. Find out electric field intensity at points C and D. [All the distances are measured in meter].](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_PHY_ELE_S01_023_Q01.png)
Electric field at point C (EA,EB are magnitudes only and arrows represent directions).
Electric field due to positive charge is away from it while due to negative charge, it is towards the charge. It is clear that E(B)>EA.
∴ENet=(EB−EA) towards negative X-axis
=K(2μC)(√2)2−K(2μC)(3√2)2 towards negative X-axis =8000(−ˆi)N/C
Electric field at point D :
Since magnitude of charges are same and also AD=BD
So, EA=EB
Vertical components of →EA and →EB cancel each other while horizontal components are in the same direction.
So, Enet=2EAcosθ=2.K(2μC)22cos45∘
=K×10−6√2=9000√2ˆiN/C.


Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Two point charges 3μC and 2.5μC are placed at point A (1, 1, 2)m and B (0, 3, -1)m respectively. Find out electric field intensity at point C(3, 3, 3)m.
View SolutionCharge 2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be somewhere

View SolutionTwo point charges2μC and 8μC areplaced 12 cm apart. Find the position of the point where the electric field intensity will be zero.
View SolutionTwo charges 10μCand−10μC are placed at points A.andB separated by a distance of 10 cm. Find the electric. field at a point P on the perpendicular bisector of AB at. a distance of 12 cm from its middle point.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).

View SolutionTwo charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
View SolutionPositive and negative charges of 1μC each are placed at two points as shown in the figure. Find the potential difference between A and B
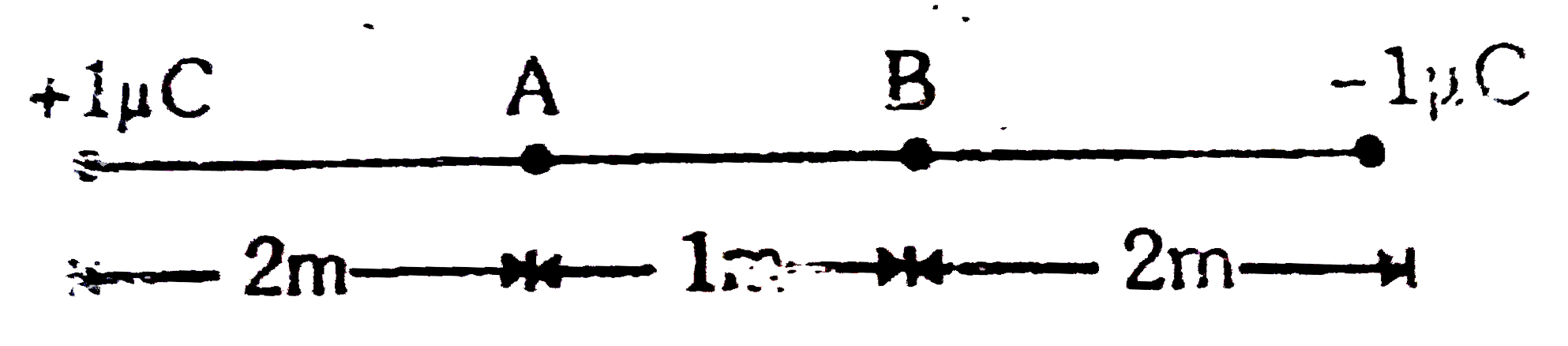
View SolutionIf three infinite charged sheets of uniform surface charge densities σ,2σ and −4σ are placed as shown in figure, then find out electric field intensities at points A, B, C and D.

View SolutionTwo point charges +10−7C and −10−7C are placed at A and B 20 cm apart as shown in the figure. Calculate the electric field at C, 20 cm apart from both A and B.
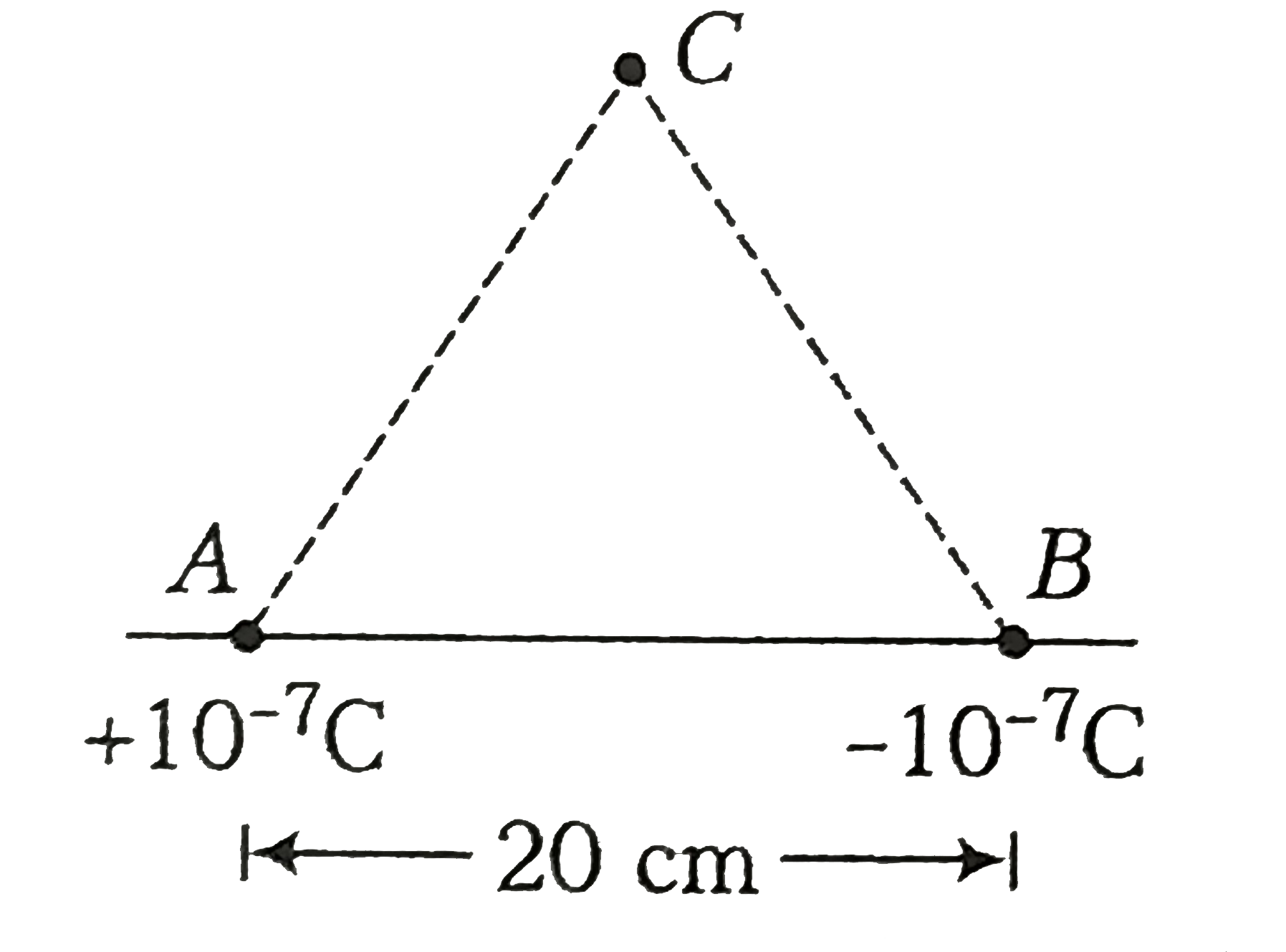
View Solution
