Consider an infinite plane sheet of mass with surface mass density σ. The gravitational field intensity at a point P at perpendicular distance r from such a sheet is
A. Zero
B. −σG
C. 2πσG
D. −4πσG
Zero
−σG
2πσG
−4πσG
To solve the problem of finding the gravitational field intensity at a point P at a perpendicular distance r from an infinite plane sheet with surface mass density σ, we can follow these steps:
1. Understand the Setup:
- We have an infinite plane sheet with surface mass density σ.
- We need to find the gravitational field intensity at a point P located at a perpendicular distance r from the sheet.
2. Use Gauss's Law for Gravity:
- According to Gauss's law for gravity, the gravitational field (g) due to a mass distribution can be determined using the concept of gravitational flux.
- The gravitational flux (Φ) through a closed surface is proportional to the enclosed mass (M) within that surface.
3. Choose a Gaussian Surface:
- For an infinite plane sheet, we can consider a cylindrical Gaussian surface that intersects the sheet. The cylinder has its flat surfaces parallel to the sheet and is symmetric about the sheet.
4. Calculate the Enclosed Mass:
- The mass enclosed by the Gaussian surface is given by:
\(
M = \sigma \cdot A
\)
where A is the area of the flat surface of the cylinder.
5. Determine the Gravitational Flux:
- The gravitational flux through the cylindrical surface is given by:
\(
\Phi = g \cdot A
\)
where g is the gravitational field intensity.
6. Apply Gauss's Law:
- According to Gauss's law, the gravitational flux is also equal to:
\(
\Phi = -\frac{GM}{r^2}
\)
- For our setup, since the gravitational field is uniform and directed downwards, we can write:
\(
\Phi = g \cdot A = -4\pi G \cdot \sigma \cdot A
\)
7. Equate the Two Expressions:
- Setting the two expressions for gravitational flux equal gives:
\(
g \cdot A = -4\pi G \cdot \sigma \cdot A
\)
8. Solve for Gravitational Field Intensity (g):
- Dividing both sides by A (assuming A ≠ 0):
\(
g = -4\pi G \cdot \sigma
\)
9. Final Result:
- Therefore, the gravitational field intensity at point P is:
\(
g = -2\pi G \cdot \sigma
\)
Conclusion:
The correct answer is C. −2πGσ.
- We have an infinite plane sheet with surface mass density σ.
- We need to find the gravitational field intensity at a point P located at a perpendicular distance r from the sheet.
- According to Gauss's law for gravity, the gravitational field (g) due to a mass distribution can be determined using the concept of gravitational flux.
- The gravitational flux (Φ) through a closed surface is proportional to the enclosed mass (M) within that surface.
- For an infinite plane sheet, we can consider a cylindrical Gaussian surface that intersects the sheet. The cylinder has its flat surfaces parallel to the sheet and is symmetric about the sheet.
- The mass enclosed by the Gaussian surface is given by:
\(
M = \sigma \cdot A
\)
where A is the area of the flat surface of the cylinder.
- The gravitational flux through the cylindrical surface is given by:
\(
\Phi = g \cdot A
\)
where g is the gravitational field intensity.
- According to Gauss's law, the gravitational flux is also equal to:
\(
\Phi = -\frac{GM}{r^2}
\)
- For our setup, since the gravitational field is uniform and directed downwards, we can write:
\(
\Phi = g \cdot A = -4\pi G \cdot \sigma \cdot A
\)
- Setting the two expressions for gravitational flux equal gives:
\(
g \cdot A = -4\pi G \cdot \sigma \cdot A
\)
- Dividing both sides by A (assuming A ≠ 0):
\(
g = -4\pi G \cdot \sigma
\)
- Therefore, the gravitational field intensity at point P is:
\(
g = -2\pi G \cdot \sigma
\)
The correct answer is C. −2πGσ.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems22videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)9videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
Similar Questions
Consider an infinite plane sheet of mass with surface mass density σ. The gravitational field intensity at a point P at perpendicular distance r from such a sheet is
A. Zero
B. −σG
C. 2πσG
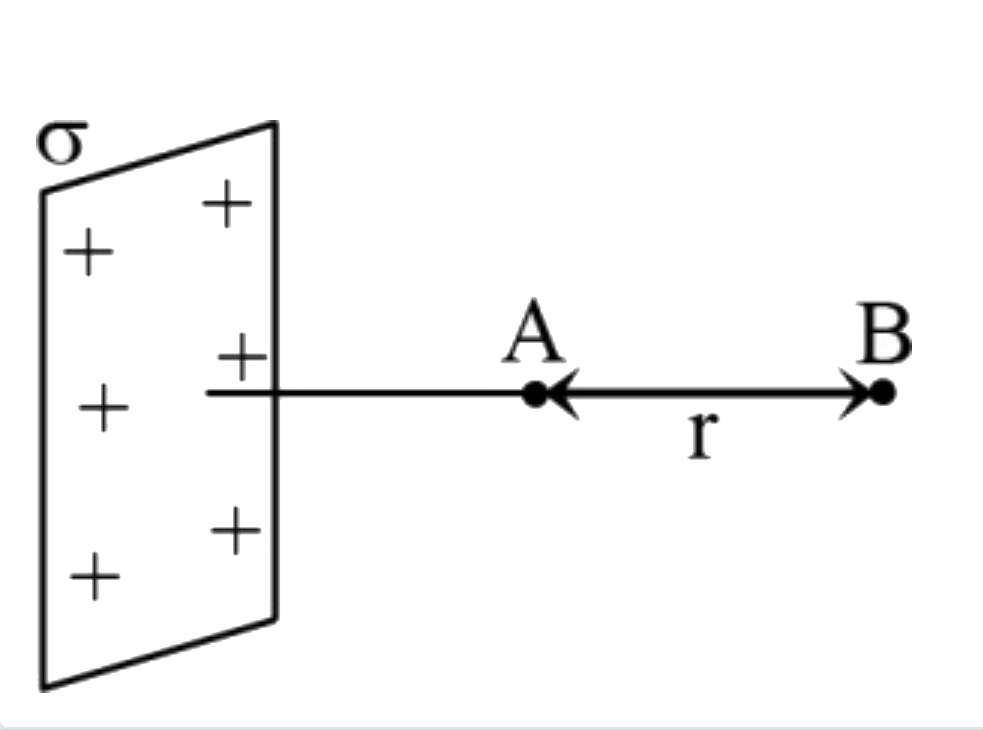
D. −4πσGView SolutionAn infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
 View Solution
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the center.
View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionIf gravitational field Intensity is E at distance R/2 outside from then surface of a thin shell of radius R , the gravitational field intensity at distance R/2 from its centre is
View Solution

