Two point charges q1(√10μC) and q2(−25μC) are placed on the x-axis at x = 1 m and x = 4 m respectively. The electric field (in V/m) at a point y =3 m on y-axis is,
[take 14π∈0=9×109Nm2C−2]
a)(63ˆi−27ˆj)×102
b)(−63ˆi+27ˆj)×102
c)(81ˆi−81ˆj)×102
d)(−81ˆi+81ˆj)×102
To find the electric field at the point (0, 3) m on the y-axis due to the two point charges q1 and q2, we will follow these steps:
Step 1: Identify the charges and their positions
- q1=√10μC is located at (1,0) m.
- q2=−25μC is located at (4,0) m.
Step 2: Calculate the distances from the charges to the point (0, 3)
- For q1:
r1=√(1−0)2+(0−3)2=√1+9=√10m
- For q2:
r2=√(4−0)2+(0−3)2=√16+9=√25=5m
Step 3: Calculate the electric field due to q1
The electric field E1 due to a point charge is given by:
E=14πϵ0|q|r2
Substituting the values for q1:
E1=14πϵ0√10×10−6(√10)2=14πϵ0√10×10−610
E1=9×109×√10×10−610=9×103√10V/m
Step 4: Determine the direction of E1
The electric field E1 points away from q1 since it is a positive charge. The components of E1 are:
- E1x=−E1⋅1√10=−9×103
- E1y=E1⋅3√10=9×103⋅3√10
Step 5: Calculate the electric field due to q2
For q2:
E2=14πϵ025×10−652=9×109×25×10−625=9×103V/m
Step 6: Determine the direction of E2
The electric field E2 points towards q2 since it is a negative charge. The components of E2 are:
- E2x=E2⋅45=9×103⋅45=7.2×103
- E2y=−E2⋅35=−9×103⋅35=−5.4×103
Step 7: Sum the electric fields
Now we can find the resultant electric field Er:
Erx=E1x+E2x=−9×103+7.2×103=−1.8×103V/m
Ery=E1y+E2y=9×103−5.4×103=3.6×103V/m
Step 8: Final Result
The resultant electric field at the point (0, 3) m is:
Er=√E2rx+E2ry=√(−1.8×103)2+(3.6×103)2
Calculating this gives:
Er=√3.24×106+12.96×106=√16.2×106≈4.02×103V/m
- q1=√10μC is located at (1,0) m.
- q2=−25μC is located at (4,0) m.
- For q1:
r1=√(1−0)2+(0−3)2=√1+9=√10m
r2=√(4−0)2+(0−3)2=√16+9=√25=5m
The electric field E1 due to a point charge is given by:
E=14πϵ0|q|r2
Substituting the values for q1:
E1=14πϵ0√10×10−6(√10)2=14πϵ0√10×10−610
E1=9×109×√10×10−610=9×103√10V/m
The electric field E1 points away from q1 since it is a positive charge. The components of E1 are:
- E1x=−E1⋅1√10=−9×103
- E1y=E1⋅3√10=9×103⋅3√10
For q2:
E2=14πϵ025×10−652=9×109×25×10−625=9×103V/m
The electric field E2 points towards q2 since it is a negative charge. The components of E2 are:
- E2x=E2⋅45=9×103⋅45=7.2×103
- E2y=−E2⋅35=−9×103⋅35=−5.4×103
Now we can find the resultant electric field Er:
Erx=E1x+E2x=−9×103+7.2×103=−1.8×103V/m
Ery=E1y+E2y=9×103−5.4×103=3.6×103V/m
The resultant electric field at the point (0, 3) m is:
Er=√E2rx+E2ry=√(−1.8×103)2+(3.6×103)2
Er=√3.24×106+12.96×106=√16.2×106≈4.02×103V/m
Similar Questions
Two point charges 3μC and 2.5μC are placed at point A (1, 1, 2)m and B (0, 3, -1)m respectively. Find out electric field intensity at point C(3, 3, 3)m.
View SolutionPoint charge q1=2μC and q2=−1μC are kept at points x=0 and x=6 respectively. Electrical potential will be zero at points
View SolutionFour points charges -q,+q,+q and -q are placed on y-axis at y=-2d, y=-d,y=+d and y=+2d, respectively. The magnitude of the electric field E at a point on the x-axis at x=D, with D>>d, will behave as :
View Solution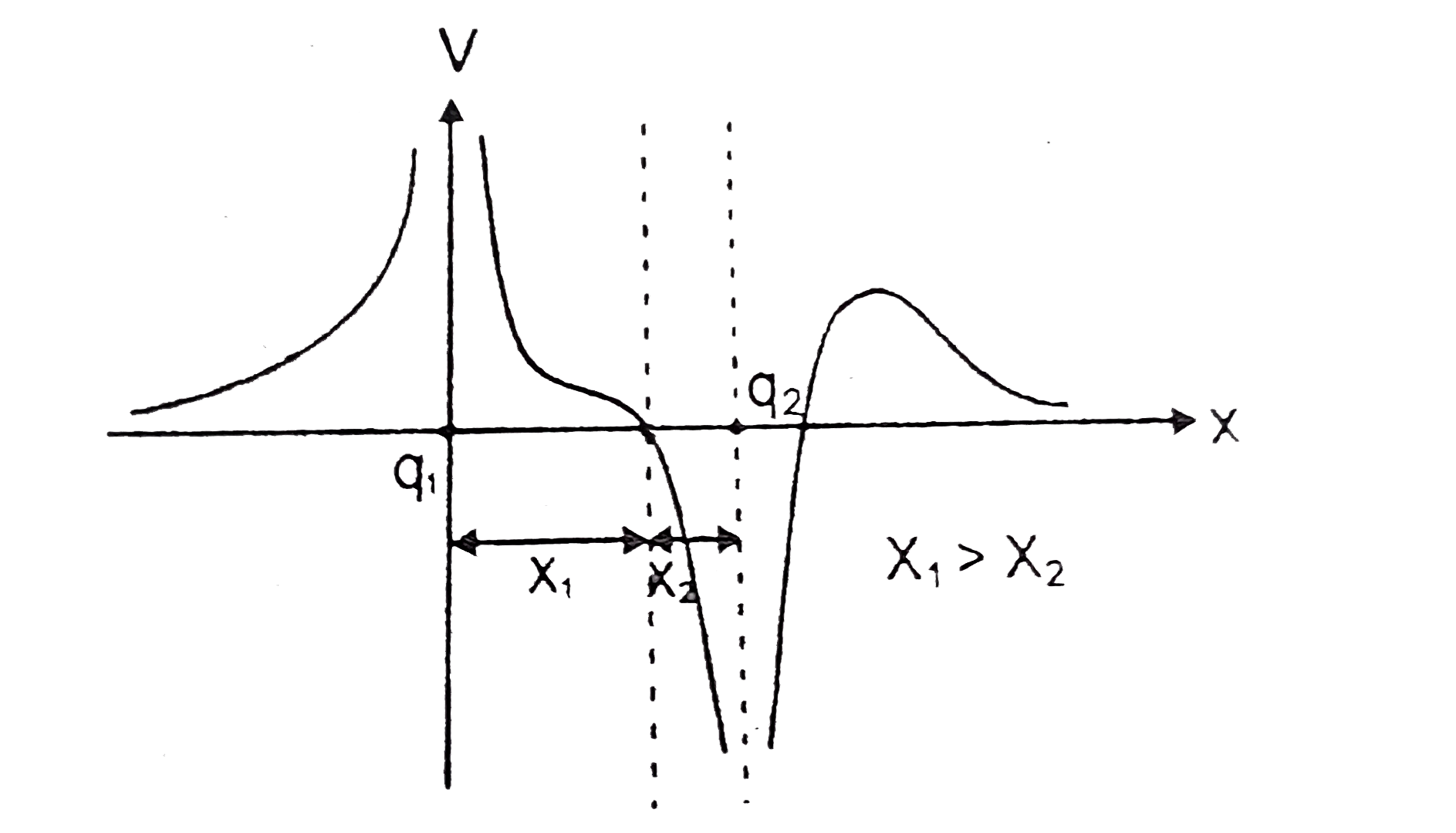
Two point charges (q1 and q2) are placed on x-axis, figure shows graph potential (V) on x-axis. With x-co-ordinate:
View SolutionWhat is the magnitude of a point charge due to which the electric field 30cm away the magnitude 2?
[1/4πε0=9×109Nm2/C2]
View SolutionPoint charges +4q,−q and +4q are kept on the x-axis at points x=0,x=a and x=2a respectively, then
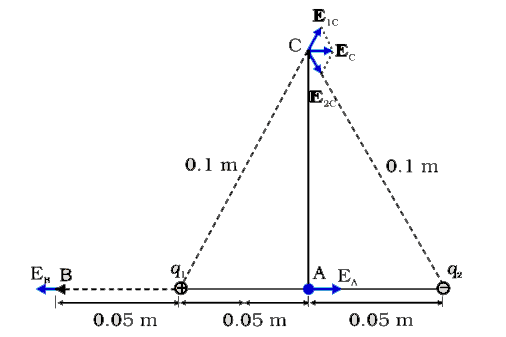
View SolutionTwo point charges q1andq2, of magnitude +10–8Cand–10–8C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.
View SolutionIf the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
View SolutionTwo point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
View SolutionTwo charges of 4μC each are placed at the corners A and B of an equilaternal triangle of side length 0.2m in air. The
electric potential at C is [14πε0=9×109N−m2C2]
View Solution