The electric field near a conducting surface having a uniform surface charge denstiy σ is given by
(a) σε0 and is parallel to the surface
(b) 2σε0
(c) σε0 and is normal to the surface
(d) 2σε0 and is normal to the surface
The correct Answer is:C
To solve the problem of finding the electric field near a conducting surface with a uniform surface charge density σ, we can follow these steps:
1. Understanding the Problem:
We have a conducting surface with a uniform surface charge density σ. We need to determine the electric field E near this surface.
2. Choosing a Gaussian Surface:
To apply Gauss's law, we will consider a Gaussian surface. A suitable choice is a cylindrical Gaussian surface that straddles the conducting surface. This surface will have one flat face inside the conductor and one flat face outside.
3. Applying Gauss's Law:
According to Gauss's law, the electric flux ΦE through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
ΦE=Qϵ0
The electric flux ΦE is given by:
ΦE=E⋅A
where E is the electric field and A is the area of the Gaussian surface.
4. Calculating the Charge Enclosed:
The charge Q enclosed by the Gaussian surface can be calculated using the surface charge density σ:
Q=σ⋅A
5. Setting Up the Equation:
Substituting the expression for Q into Gauss's law gives:
E⋅A=σ⋅Aϵ0
6. Solving for the Electric Field E:
We can cancel A from both sides (assuming A≠0):
E=σϵ0
7. Direction of the Electric Field:
The electric field E is directed perpendicular to the surface of the conductor and away from the surface if the charge is positive.
Final Answer:
The electric field near a conducting surface having a uniform surface charge density σ is given by:
E=σϵ0
We have a conducting surface with a uniform surface charge density σ. We need to determine the electric field E near this surface.
To apply Gauss's law, we will consider a Gaussian surface. A suitable choice is a cylindrical Gaussian surface that straddles the conducting surface. This surface will have one flat face inside the conductor and one flat face outside.
According to Gauss's law, the electric flux ΦE through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
ΦE=Qϵ0
The electric flux ΦE is given by:
ΦE=E⋅A
where E is the electric field and A is the area of the Gaussian surface.
The charge Q enclosed by the Gaussian surface can be calculated using the surface charge density σ:
Q=σ⋅A
Substituting the expression for Q into Gauss's law gives:
E⋅A=σ⋅Aϵ0
We can cancel A from both sides (assuming A≠0):
E=σϵ0
The electric field E is directed perpendicular to the surface of the conductor and away from the surface if the charge is positive.
The electric field near a conducting surface having a uniform surface charge density σ is given by:
E=σϵ0
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
The magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View SolutionElectric field intensity at a point due to an infinite sheet of charge having surface charge density σ is E.If sheet were conducting electric intensity would be
View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionAn infinitely large non-conducting plane of uniform surface charge density σ has circular aperture of certain radius carved out from it. The electric field at a point which is at a distance 'a' from the centre of the aperture (perpendicular to the plane) is σ2√2∈0. Find the radius of aperture :
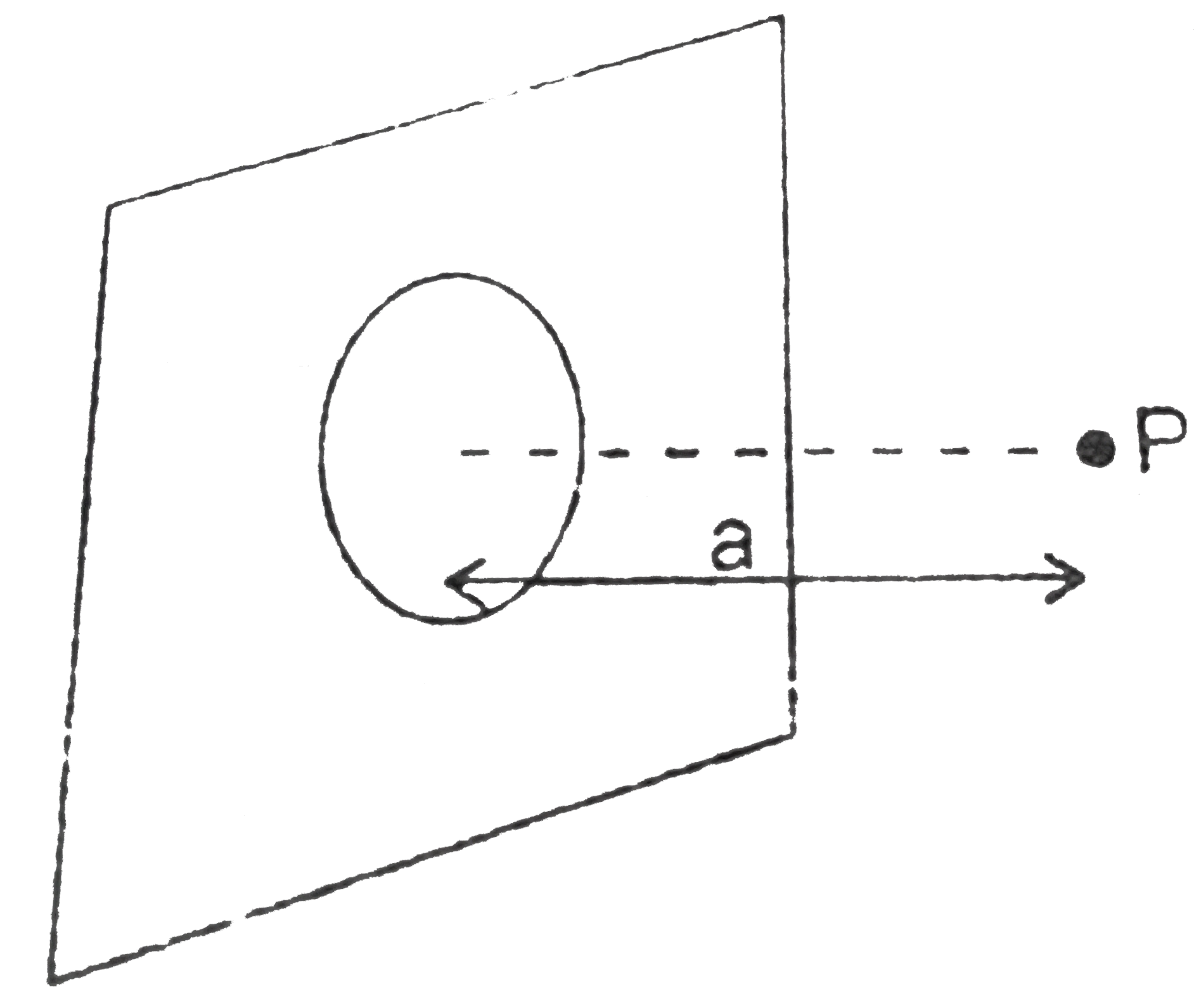
View Solution
The quarter disc of radius R (see figure) has a uniform surface charge density σ.
(a) Find electric potential at a point (O,O,Z)
(b). Find the Z component of electrif field at (O,O,Z)
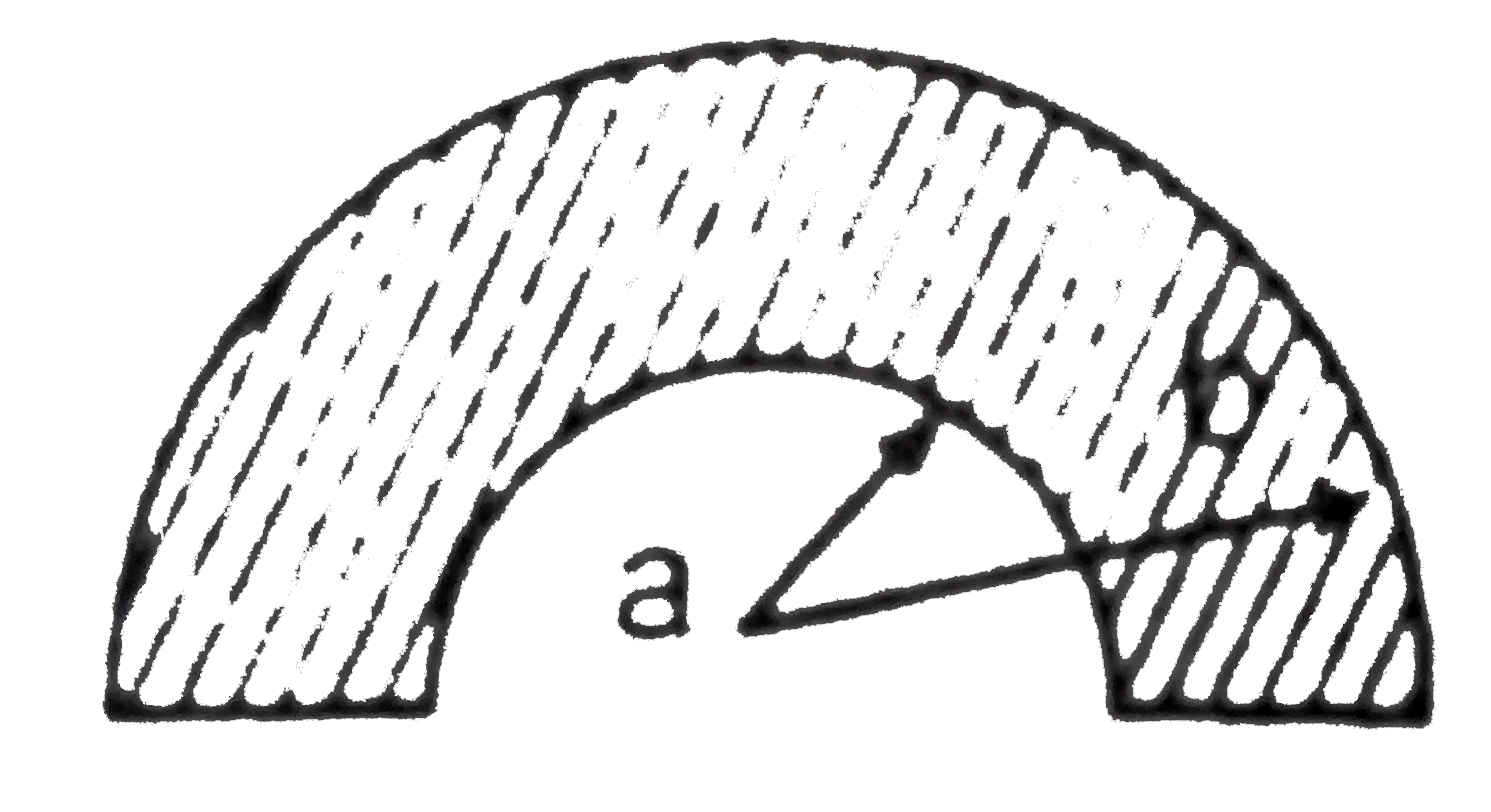
View SolutionA non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
View SolutionThere are two infinite plane sheets each having uniform surface charge density +σC/m2 They are inclined to each other at an angle 30∘as shown in the figure. Electric field at any arbitrary point P is:

View SolutionThere are two infinite plane sheets each having uniform surface charge density +σC/m2 They are inclined to each other at an angle 30∘as shown in the figure. Electric field at any arbitrary point P is:

View SolutionTwo infinite, non-conducting sheets of charge are parallel to each other, as shown in figure. The sheet on the left has a uniform surface charge density σ, and the one on the right has a uniform charge density −σ. Calculate the electric field at points (a) to the left of, (b) in between, and (c) to the right of the two sheets.

View Solution
