A certain dye absorbs 4000 Å and fluoresces at 8000 Å. These being wavelengths of maximum absorption that under given conditions 50 % of the absorbed energy is emitted. Calculate the ratio of the no. of quanta emitted to the number absorbed.
The correct Answer is:1
To solve the problem, we need to calculate the ratio of the number of quanta emitted (N_E) to the number of quanta absorbed (N_A) by a dye that absorbs a specific wavelength and fluoresces at another wavelength.
1. Identify the Given Data:
- Wavelength of maximum absorption (λ_absorbed) = 4000 Å
- Wavelength of maximum emission (λ_emitted) = 8000 Å
- Percentage of absorbed energy emitted = 50%
2. Use the Formula for Energy of a Photon:
The energy (E) of a photon can be calculated using the formula:
E=H⋅Cλ
where:
- H = Planck's constant (6.626 x 10^-34 J·s)
- C = Speed of light (3 x 10^8 m/s)
- λ = Wavelength in meters
3. Calculate the Energy of Absorbed and Emitted Photons:
- Energy absorbed (E_A) at 4000 Å:
EA=H⋅Cλabsorbed=H⋅C4000×10−10 m
- Energy emitted (E_E) at 8000 Å:
EE=H⋅Cλemitted=H⋅C8000×10−10 m
4. Relate the Number of Quanta Emitted and Absorbed:
Since 50% of the absorbed energy is emitted, we can express this relationship as:
EE=0.5⋅EA
5. Substituting the Energy Values:
H⋅C8000×10−10=0.5⋅H⋅C4000×10−10
6. Canceling Common Terms:
Since H and C are constants, they can be canceled out from both sides:
18000=0.5⋅14000
7. Simplifying the Equation:
Rearranging gives:
18000=18000
This confirms that the relationship holds.
8. Finding the Ratio of Quanta:
The number of quanta emitted (N_E) and absorbed (N_A) can be expressed as:
NE=EEEphotonandNA=EAEphoton
Thus, the ratio of the number of quanta emitted to the number absorbed is:
NENA=EEEA=0.5⋅EAEA=0.5
9. Final Ratio Calculation:
Since we are looking for the ratio of quanta emitted to absorbed:
NENA=11
Conclusion:
The ratio of the number of quanta emitted to the number absorbed is 1:1.
- Wavelength of maximum absorption (λ_absorbed) = 4000 Å
- Wavelength of maximum emission (λ_emitted) = 8000 Å
- Percentage of absorbed energy emitted = 50%
The energy (E) of a photon can be calculated using the formula:
E=H⋅Cλ
where:
- H = Planck's constant (6.626 x 10^-34 J·s)
- C = Speed of light (3 x 10^8 m/s)
- λ = Wavelength in meters
- Energy absorbed (E_A) at 4000 Å:
EA=H⋅Cλabsorbed=H⋅C4000×10−10 m
- Energy emitted (E_E) at 8000 Å:
EE=H⋅Cλemitted=H⋅C8000×10−10 m
Since 50% of the absorbed energy is emitted, we can express this relationship as:
EE=0.5⋅EA
H⋅C8000×10−10=0.5⋅H⋅C4000×10−10
Since H and C are constants, they can be canceled out from both sides:
18000=0.5⋅14000
Rearranging gives:
18000=18000
This confirms that the relationship holds.
The number of quanta emitted (N_E) and absorbed (N_A) can be expressed as:
NE=EEEphotonandNA=EAEphoton
Thus, the ratio of the number of quanta emitted to the number absorbed is:
NENA=EEEA=0.5⋅EAEA=0.5
Since we are looking for the ratio of quanta emitted to absorbed:
NENA=11
The ratio of the number of quanta emitted to the number absorbed is 1:1.
Topper's Solved these Questions
Similar Questions
A certain day absorbs lights of λ=400 nm and then fluorescence light of wavelength 500 mn. Assuming that under given condition 40% of the absorbed energy is re-emitted as fluorescence, calculate the ratio of quanta obserbed to number of quanta emitted out.
View SolutionA certain dye absorbs light of cerain wavelength and then fluorescence light of wavelength 5000 Å.Assuming that under given conditions , 50% of the absorbed energy is re-emitted out as fluorescence and the ratio of number of quanta emitted out to the number of quanta absorbed is 5:8, find the wavelength of absorbed light (in Å) : [hc=12400 eVÅ]
View SolutionA dye obsorbs light of λ=4530Å and then flaorescences light of 5000Å .Assuming that uinder given condition 47% of the obserbed energy is re-emited out so flaurescence , calculate the ratio of quants emitted out to the number of quanta obserbed
View SolutionAn electron in a hydrogen atom in its ground state absorbs energy equal to ionisation energy of Li+2. The wavelength of the emitted electron is :-
View SolutionAn electron in the first excited state of H atom absorbed a photon and further excited. The de broglie wavelength of the electron in this state is found to be 13.4 Å. Find the wavelength of the photon absorbed by the electron in angstroms. Also find the longest and the shortest wavelength emitted when this electron de-excited back to the ground state.
View SolutionA gas absorbs a photon of 310nm and emits three photons.
If energy of emitted photons is in the ratio 1:2:1 then select correct statement(s) :
View SolutionIn hydrogen atom, an electron in its ground state absorbs two times of the energy as if requires escaping (13.6 eV) from the atom. The wavelength of the emitted electron will be
View SolutionA photon of 300nm is absorbed by a gas which then re-emits photon .One re-emited photon has a wavelength of 400nm .Calculate the energy of the other photon re-emitted not
View SolutionTwo bulbs 'A' and 'B' emit red light and yellow light at 8000 "Å" and 4000 "Å" respectively. The number of photons emitted by both the bulbs per second is the same. If the red bulb is labelled as 100 watts, find the wattage of the yellow bulb.
View SolutionA point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
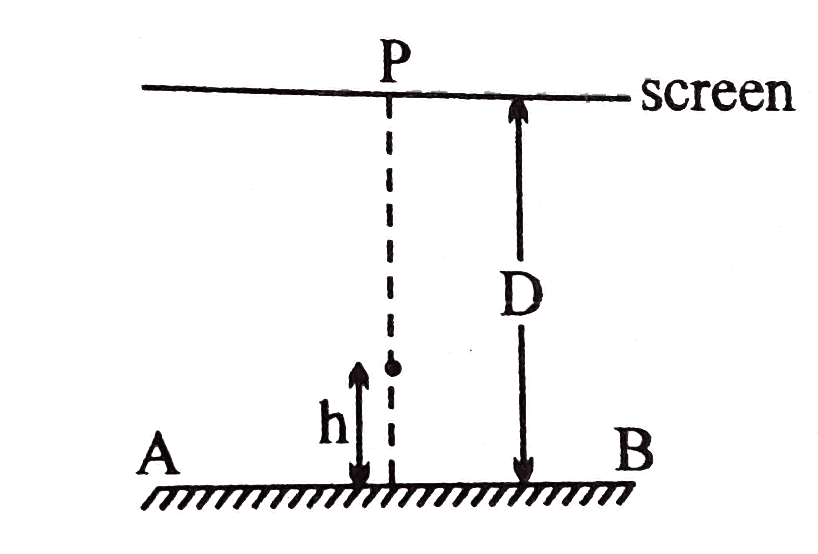
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
View Solution
