Let the speed of the planet at the perihelion P in figure be vP and the Sun planet distance SP be rP. Relater rP,vP to the corresponding quantities at the aphelion (rA,vA). Will the planet take equal times to transverse BAC and CPB?

The magnitude of the angular momentum at P is Lp=mPrpup. Since inspection tells us that rp and vp are mutually perpendicular. Similarly . LA=mprA.vA. From angular momentum conservation
mprpvp=mprAvA
or vpvA=rArp
The area, SBAX bounded by the elipse and the raidus vectors SB and SC is large than SBPC in Fig. 9.1 From kepler's second law, equal areas are swept in equal times. Hence the planat will take a longer time to traverse BAC than CPB.
Topper's Solved these Questions
Similar Questions
A: The speed of a planet is maximum at perihelion .
R : The angular momentum of a planet about centre of sun is conserved .
View SolutionLet V and I be the readings of the voltmeter and the ammeter respectively as shown in the figure. Let RV and RA be their corresponding resistancce Therefore,
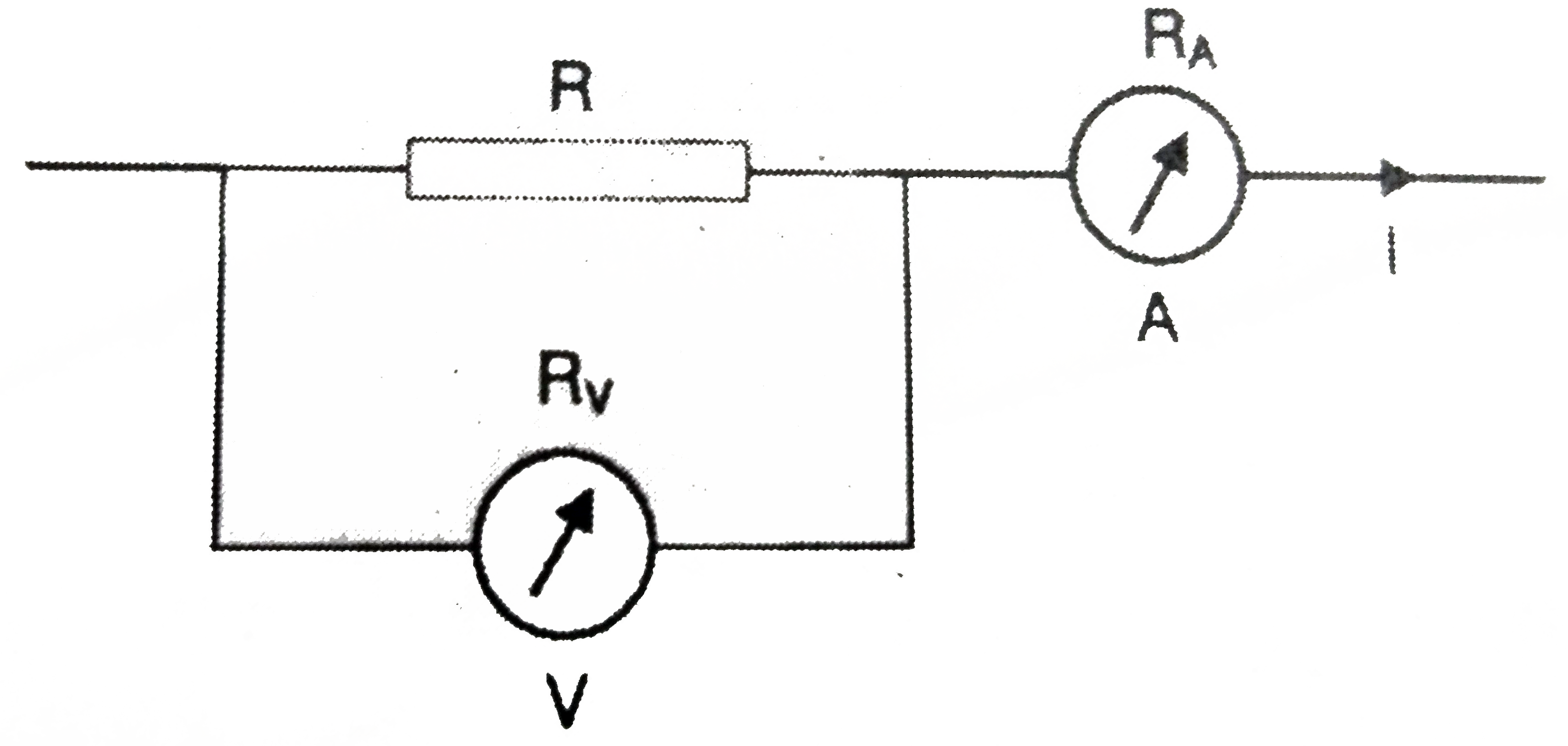
View Solution
Knowledge Check
A planet orbits the sun in an elliptical path as shown in the figure. Let vp and vA be spped of the planet when at perohelion and aphelion respectively. Which of the following relations is correct ?
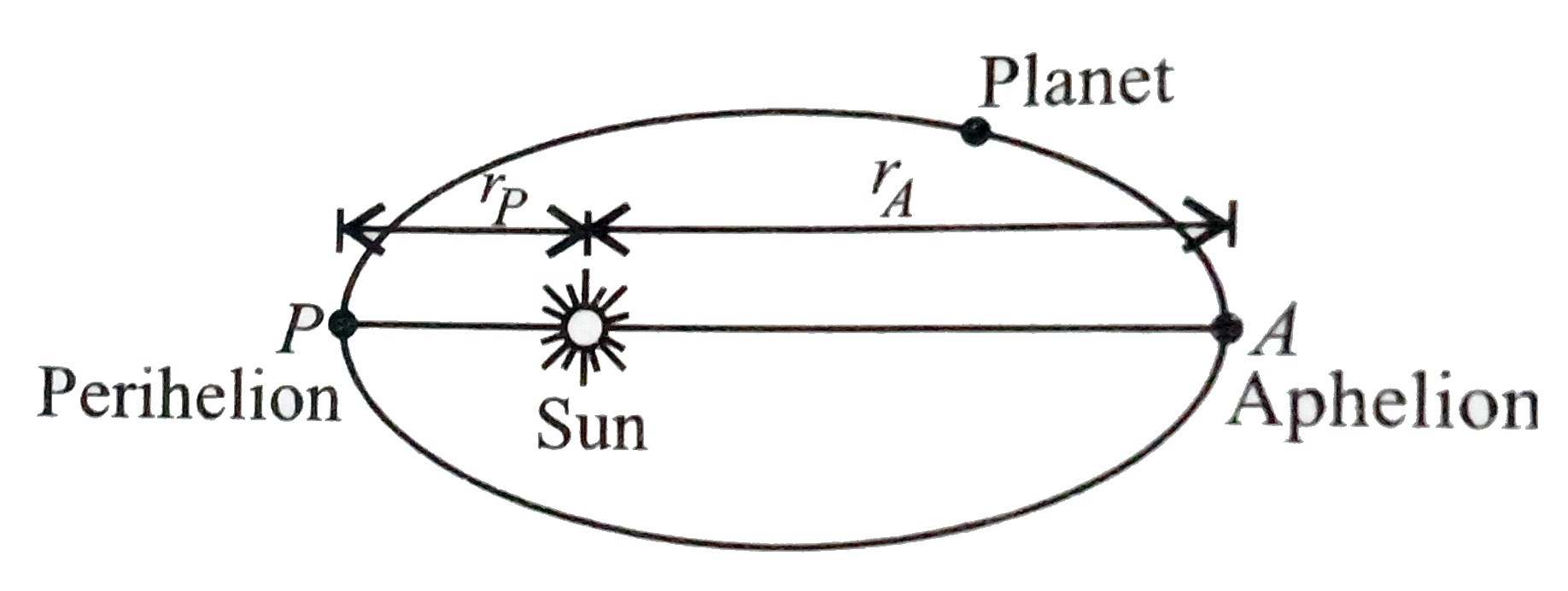 ArprA=vAvpBrprA=vpvACrprA=√vpvADrprA=√vAvp
ArprA=vAvpBrprA=vpvACrprA=√vpvADrprA=√vAvpA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
Find VP−VQ in the circuit shown in figure.
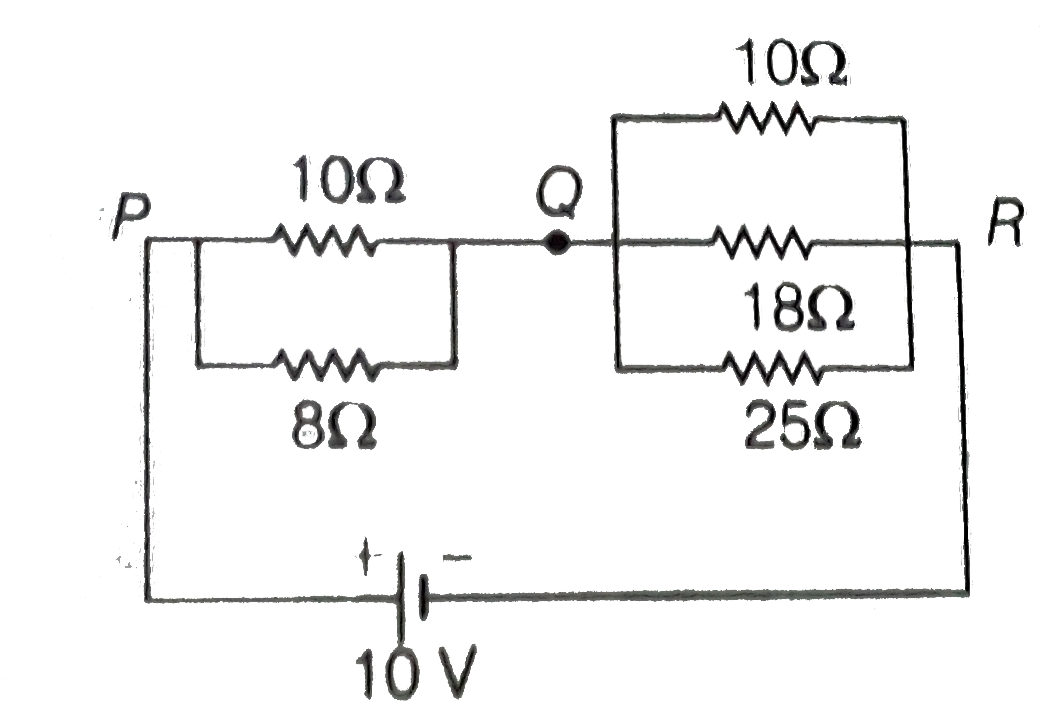
View SolutionSpeed of a planet in an ellioptical orbit with semimajor axis a about sun of mass M at a distance r from sun is
View SolutionThe radius of a planet is double that of earth but their average are the same. If the escape velocities at the planet and the earth are vp and ve respectively , then prove that vp=2ve.
View SolutionA satellite of mass m orbits the earth in an elliptical orbit having aphelion distance ra and perihelion distance rp. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are ra+rp2 and √rpra respectively. The angular momentum of the satellite is: (A) 2mπ(rB+rp)√rarpT (B) mπ(ra+rp)√rarp2T (C) mπ(ra+rp)√rarp4T (D) mπ(ra+rp)√rarpT
View SolutionA planet moves around the sun. It is closest to sun to sun at a distance d1 and have velocity v1 At farthest distance d2 its speed will be
View SolutionIn Figure, ∠PQR= ∠PRQ, then prove that ∠PQS= ∠PRT.
View Solution
