If the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, its areal velocity is :
L2m
4Lm
LM
2Lm
The correct Answer is:A
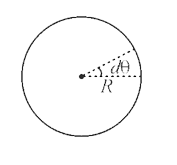
dA=12R2dθ
dAdt=12R2dθdt=R22ω
L=mR2ω
∴dAdt=R22(LmR2)=L2m i.e.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a planet revolves around the sun in a circular orbit of radius a with a speed of revolution T, then (K being a positive constant
AT=Ka2/3BT=Ka3/2CT=Ka2DT=Ka3
Find the angular momentum of a satellite of mass m moving round the earth of mass m if its orbital radius is r, assuming it to be circular. Express it in terms of G, M, m and r, where G is the universal gravitational constant ?
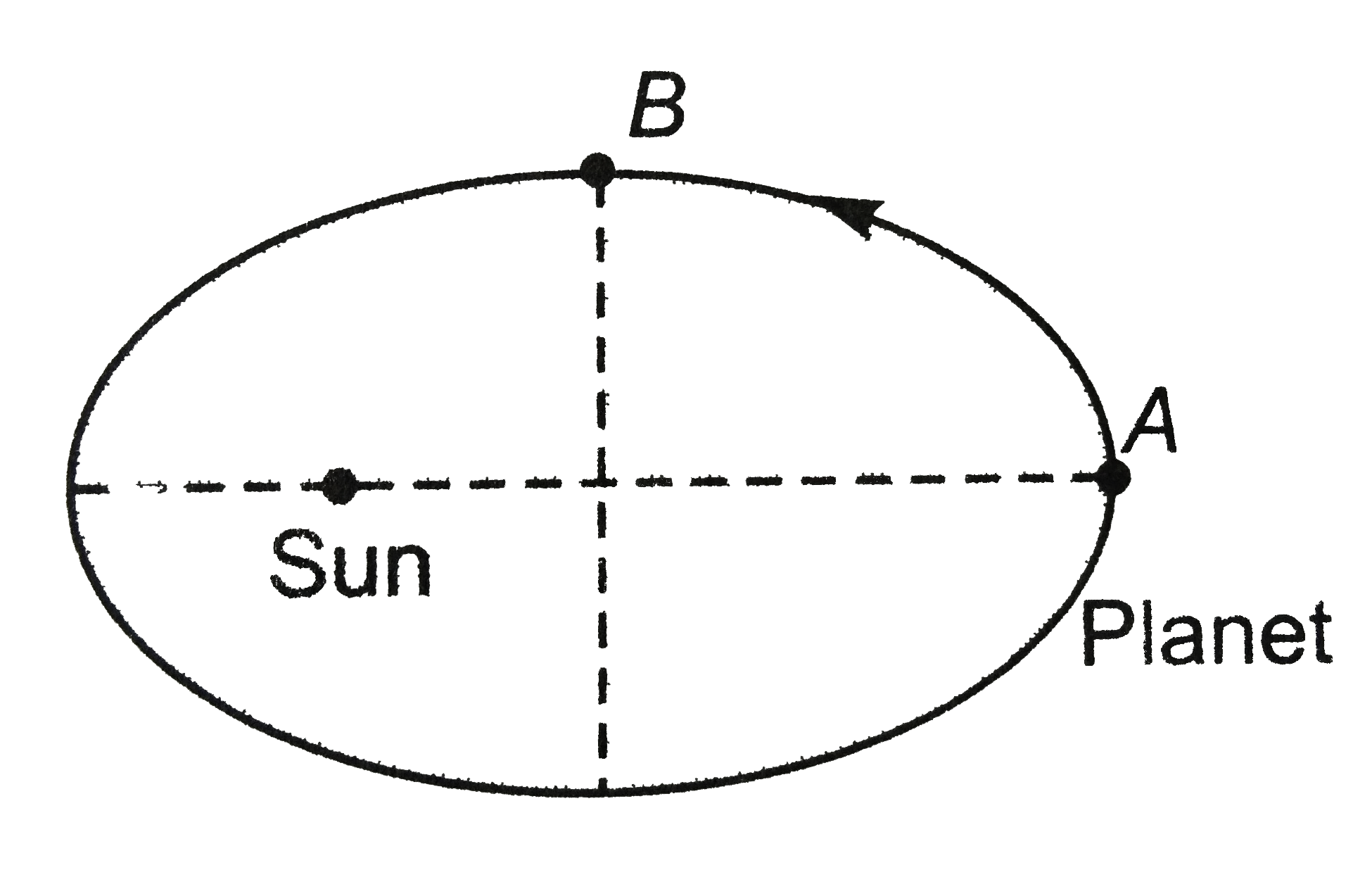
View SolutionA planet is moving round the sun in an elliptical orbit as shows. As the planet moves from A to B
View SolutionWhen a planet moves around the sun
View SolutionIdentify the incorrect statement about a planet revolving around Sun
View SolutionThe angular momentum (L) of an electron moving in a stable orbit around nucleus is
View SolutionThe satellite of mass m revolving in a circular orbit of radius r around the earth has kinetic energy E. then, its angular momentum will be
View SolutionThe earth, moving around the sun in a circular orbit, is acted upon by a force and hence work must be done on earth by this force.
View Solution