From a disc of radius R, a concentric circular portion of radius r is cut out so as to leave an annular disc of mass M. The moment of inertia of this annular disc about the axis perpendicular to its plane and passing through its centre of gravity is
12M(R2+r2)
12M(R2−r2)
12M(R4+r4)
12M'(R4−r4)
The correct Answer is:A
To find the moment of inertia of an annular disc about an axis perpendicular to its plane and passing through its center of gravity, we can follow these steps:
Step 1: Define the Problem
We have a disc of radius R with a concentric circular portion of radius r cut out, leaving an annular disc of mass M. We need to calculate the moment of inertia I of this annular disc.
Step 2: Calculate the Mass per Unit Area
The area of the annular disc is given by the difference in the areas of the two circles:
Area=πR2−πr2=π(R2−r2)
The mass per unit area σ is then:
σ=Mπ(R2−r2)
Step 3: Consider an Elemental Ring
We will consider a thin concentric ring at a distance A from the center with thickness dA. The circumference of this ring is 2πA, and its area dA is given by:
dA=2πAdA
Step 4: Find the Elemental Mass
The elemental mass dM of the ring can be calculated using the mass per unit area:
dM=σ⋅dA=σ⋅(2πAdA)=Mπ(R2−r2)⋅(2πAdA)=2MAR2−r2dA
Step 5: Calculate the Moment of Inertia of the Elemental Ring
The moment of inertia dI of this elemental ring about the axis is given by:
dI=dM⋅A2=(2MAR2−r2dA)A2=2MA3R2−r2dA
Step 6: Integrate to Find Total Moment of Inertia
Now, we integrate dI from r to R:
I=∫RrdI=∫Rr2MA3R2−r2dA
This can be simplified as:
I=2MR2−r2∫RrA3dA
Step 7: Evaluate the Integral
The integral of A3 is:
∫A3dA=A44
Evaluating from r to R:
∫RrA3dA=(A44)Rr=R44−r44=R4−r44
Step 8: Substitute Back to Find I
Substituting back into the equation for I:
I=2MR2−r2⋅R4−r44=M(R4−r4)2(R2−r2)
Step 9: Simplify the Result
We can simplify R4−r4 using the difference of squares:
R4−r4=(R2−r2)(R2+r2)
Thus, the moment of inertia becomes:
I=M(R2+r2)2
Final Result
The moment of inertia of the annular disc about the axis perpendicular to its plane and passing through its center of gravity is:
M(R2+r2)2
We have a disc of radius R with a concentric circular portion of radius r cut out, leaving an annular disc of mass M. We need to calculate the moment of inertia I of this annular disc.
The area of the annular disc is given by the difference in the areas of the two circles:
Area=πR2−πr2=π(R2−r2)
The mass per unit area σ is then:
σ=Mπ(R2−r2)
We will consider a thin concentric ring at a distance A from the center with thickness dA. The circumference of this ring is 2πA, and its area dA is given by:
dA=2πAdA
The elemental mass dM of the ring can be calculated using the mass per unit area:
dM=σ⋅dA=σ⋅(2πAdA)=Mπ(R2−r2)⋅(2πAdA)=2MAR2−r2dA
The moment of inertia dI of this elemental ring about the axis is given by:
dI=dM⋅A2=(2MAR2−r2dA)A2=2MA3R2−r2dA
Now, we integrate dI from r to R:
I=∫RrdI=∫Rr2MA3R2−r2dA
This can be simplified as:
I=2MR2−r2∫RrA3dA
The integral of A3 is:
∫A3dA=A44
Evaluating from r to R:
∫RrA3dA=(A44)Rr=R44−r44=R4−r44
Substituting back into the equation for I:
I=2MR2−r2⋅R4−r44=M(R4−r4)2(R2−r2)
We can simplify R4−r4 using the difference of squares:
R4−r4=(R2−r2)(R2+r2)
Thus, the moment of inertia becomes:
I=M(R2+r2)2
The moment of inertia of the annular disc about the axis perpendicular to its plane and passing through its center of gravity is:
M(R2+r2)2
Similar Questions
The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through -
View SolutionThe moment of inertia of a solid sphere of radius R about an axis passing through its diameter is /. The sphere is melted and recast into a circular disc of thickness R3. The moment of inertia of this disc about an axis perpendicular to plane and passing through its centre of mass is
View Solution
Knowledge Check
From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
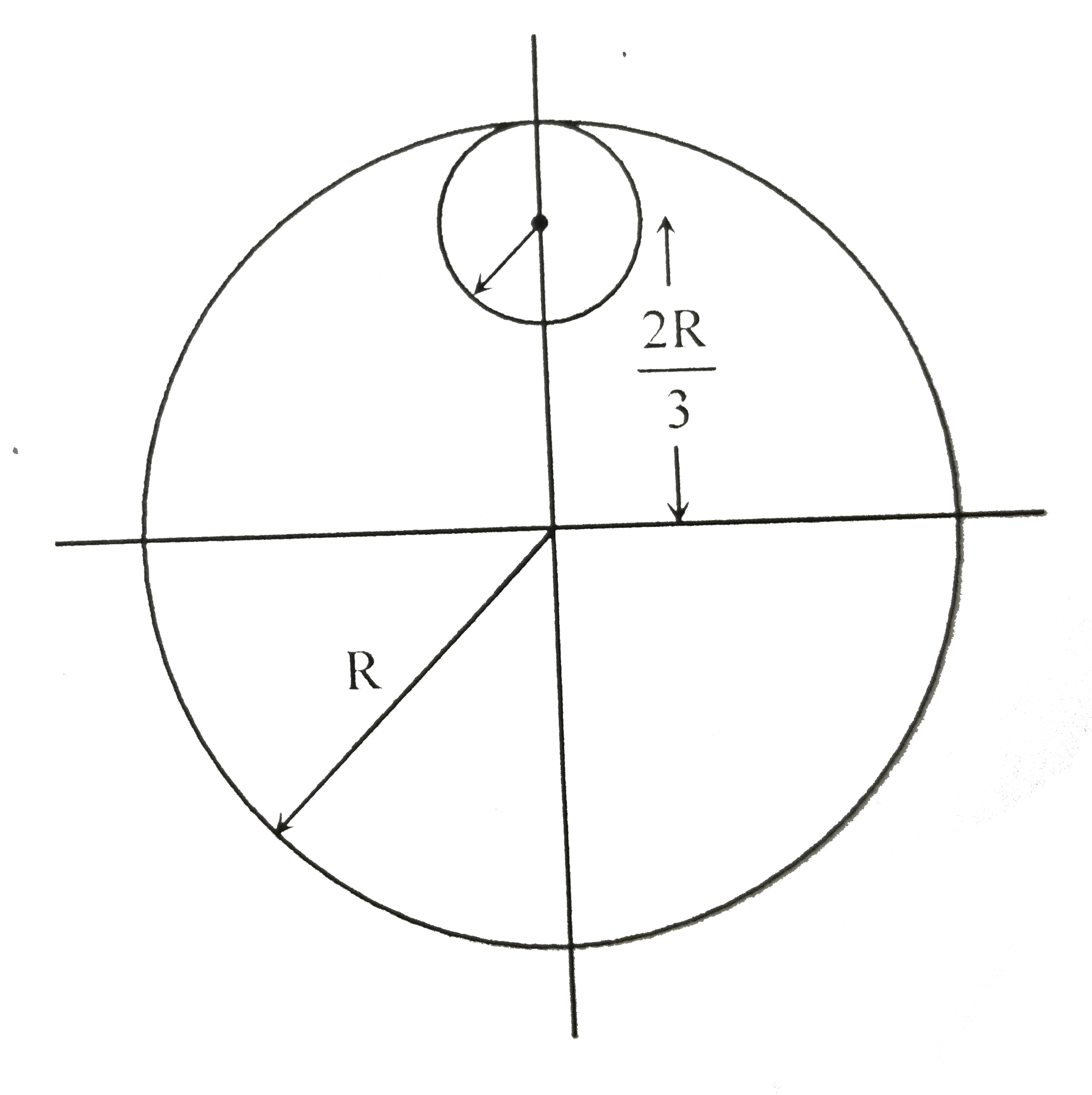 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
From a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionMoment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionFrom a disc of radius RandmassM, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of remaining part of the disc about a perependicular axis, passing through the centre ?
View SolutionThe moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
View SolutionThe moment of inertia of thin uniform circular disc about one of the diameter is I. Its moment of inertia about an axis perpendicular to the circular surface and passing through its centre is
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View Solution
