Einstein's photoelectric equation states that Ek=hv−W . In this equation Ek refers to
Kinetic energy of all ejected electrons
Mean kinetic energy of emitted electrons
Minimum kinetic energy of emitted electrons
Maximum kinetic energy of emitted electrons
The correct Answer is:D
To solve the question regarding Einstein's photoelectric equation, we need to identify what Ek refers to in the equation Ek=hν−W.
1. Understanding the Photoelectric Effect:
- The photoelectric effect occurs when light (radiation) of a certain frequency strikes the surface of a metal and causes the ejection of electrons from that surface.
2. Identifying the Components of the Equation:
- In the equation Ek=hν−W:
- Ek represents the kinetic energy of the emitted electrons.
- h is Planck's constant.
- ν (or μ) is the frequency of the incident light.
- W is the work function of the metal, which is the minimum energy required to remove an electron from the surface of the metal.
3. Relating Energy to Kinetic Energy:
- When light of frequency ν strikes the metal surface, if the energy hν of the incoming photons is greater than the work function W, electrons are ejected.
- The difference between the energy of the incoming photon hν and the work function W gives the kinetic energy Ek of the emitted electrons.
4. Conclusion:
- Therefore, Ek refers to the maximum kinetic energy of the emitted electrons when the incident light has a frequency greater than the threshold frequency.
Final Answer:
In Einstein's photoelectric equation Ek=hν−W, Ek refers to the maximum kinetic energy of the emitted electrons.
---
- The photoelectric effect occurs when light (radiation) of a certain frequency strikes the surface of a metal and causes the ejection of electrons from that surface.
- In the equation Ek=hν−W:
- Ek represents the kinetic energy of the emitted electrons.
- h is Planck's constant.
- ν (or μ) is the frequency of the incident light.
- W is the work function of the metal, which is the minimum energy required to remove an electron from the surface of the metal.
- When light of frequency ν strikes the metal surface, if the energy hν of the incoming photons is greater than the work function W, electrons are ejected.
- The difference between the energy of the incoming photon hν and the work function W gives the kinetic energy Ek of the emitted electrons.
- Therefore, Ek refers to the maximum kinetic energy of the emitted electrons when the incident light has a frequency greater than the threshold frequency.
In Einstein's photoelectric equation Ek=hν−W, Ek refers to the maximum kinetic energy of the emitted electrons.
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - LEVEL - 2
50 Videos
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - LEVEL - 2 ( Numerical value type for JEE Main )
16 Videos
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Level - 0 (Long Answer Type (5 Marks))
11 Videos
- AMINESBOOK - VMC MODULES ENGLISHCHAPTER - AMINESEXERCISE - IN CHAPTER EXERCISE H
10 Videos
- CHEMICAL BONDING & CHEMICAL STRUCTURE BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL BONDING & CHEMICAL STRUCTURE EXERCISE - IMPECCABLE
50 Videos
Similar Questions
Knowledge Check
According to Einstein's photoelectric equation , the graph between the kinetic energy of photoelectrons ejected and the frequency of incident radiation is
A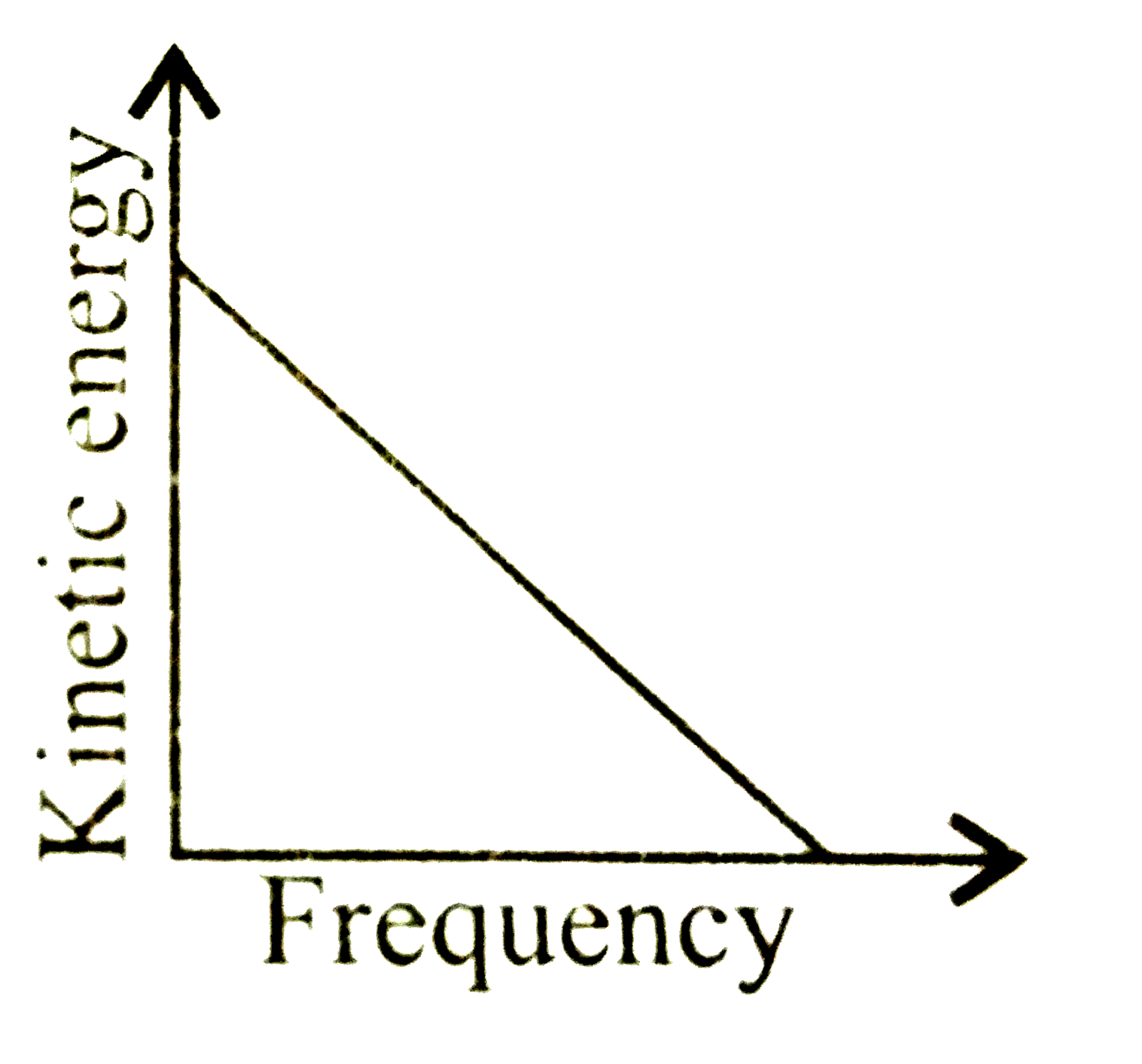 B
B C
C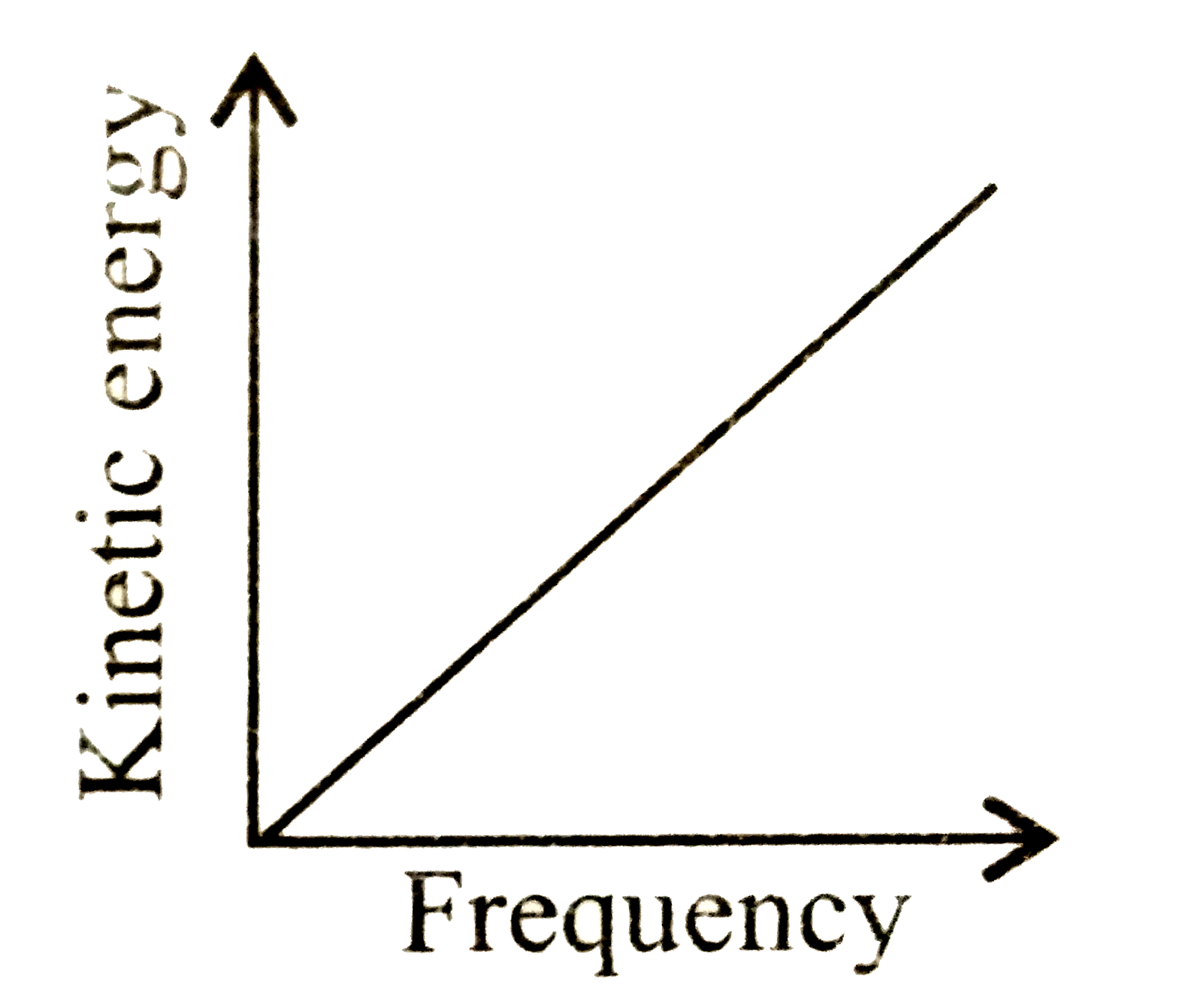 D
D
Write Einstein's photoelectric equation.
Write the three salient features observed in photoelectric effect which can be explained using this equation.
View SolutionWrite Einstein's photoelectric equation. State clearly any two salient features observe in photoelctric effect, which can be explained on the basis of the above equation.
View SolutionWrite Einstein's photoelectric equation and point out any two characteristic properties of photons on which this equation is based.
View SolutionAccording to Einstein's photoelectric equation, the graph between kinetic energy of photoelectrons ejected and the frequency of the incident radiation is :
View SolutionWhat is photoelectric effect? Mention the Einstein's photoelectric equation.
View SolutionRate of a reaction can be expressed by Arrhenius equation as:
k=Ae−Ea/RT
In this equation, Ea represents:
View Solution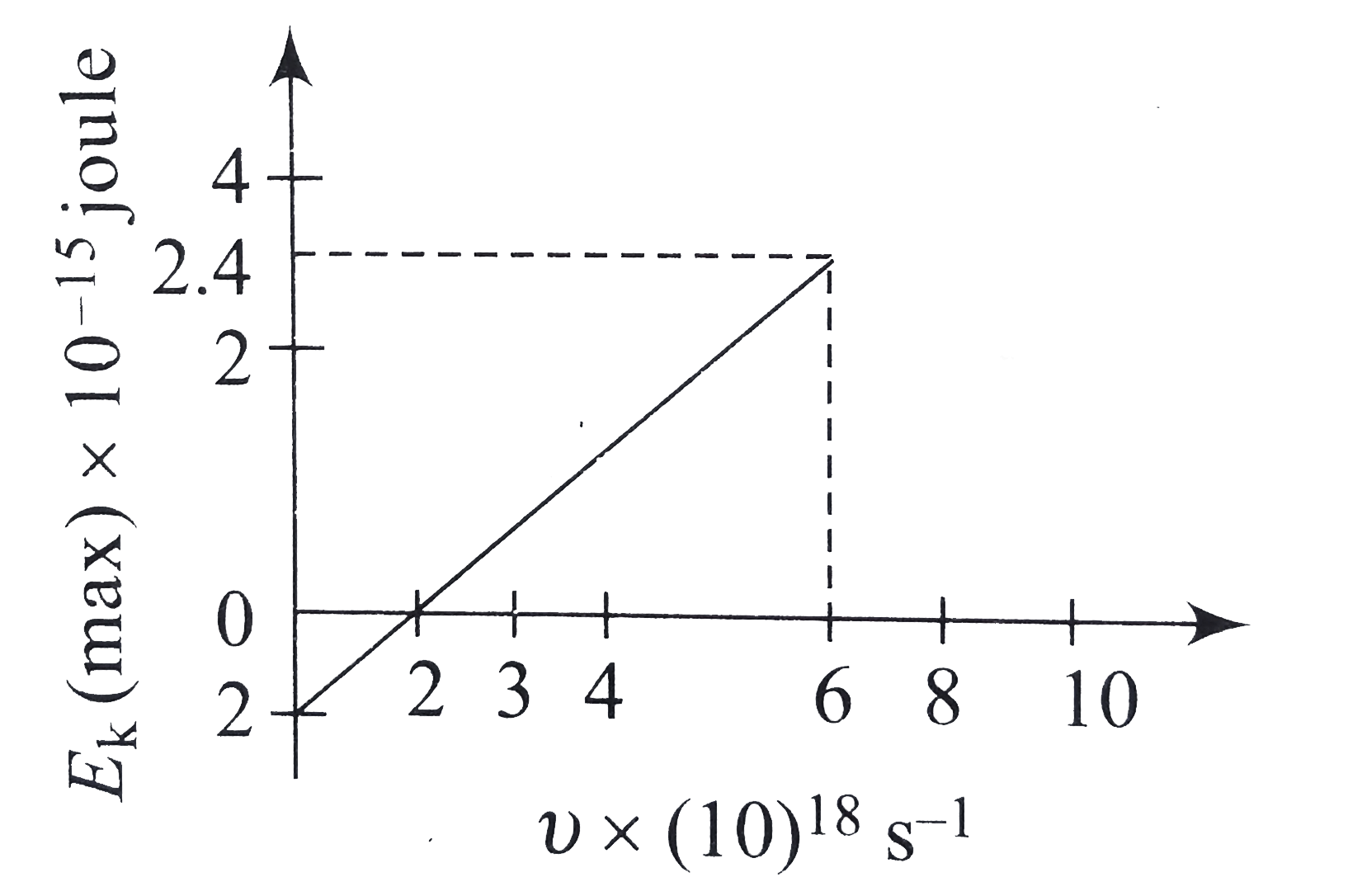
In the experiment on photoelectric effect, the graph between EK(max) and v is found to be a straight line as sshoen in fig. The threshold frequency and Planck's constant according to this graph are
View Solution
