The shortest distance between IstandVth layer of HCP arrangement is:
8√23r
4√32r
16√123r
8√32r
The correct Answer is:A
To find the shortest distance between the first and fifth layer of a Hexagonal Close-Packed (HCP) arrangement, we can follow these steps:
1. Understanding HCP Arrangement:
- In HCP, the layers are arranged in a specific manner where the first layer is above the second layer, and the third layer is directly above the first layer again, followed by the fourth and fifth layers.
2. Identifying the Layers:
- The first layer (I) and the fifth layer (V) are separated by several layers in between. To find the distance between these layers, we need to calculate the height of the layers.
3. Height of the Tetrahedron:
- In HCP, the distance between adjacent layers can be represented using the tetrahedral arrangement. The height (h) of a tetrahedron formed by the atoms can be calculated.
- The height of the tetrahedron is given by the formula:
h=2√2r2√3
4. Calculating the Distance Between Layers:
- The distance between the first and fifth layers involves four heights (since there are four layers between them).
- Therefore, the total height (H) between the first and fifth layers can be calculated as:
H=4h=4(2√2r2√3)
- Simplifying this gives:
H=8√2r2√3
5. Final Expression:
- Thus, the shortest distance between the first and fifth layers of the HCP arrangement is:
H=8√2r√3
- In HCP, the layers are arranged in a specific manner where the first layer is above the second layer, and the third layer is directly above the first layer again, followed by the fourth and fifth layers.
- The first layer (I) and the fifth layer (V) are separated by several layers in between. To find the distance between these layers, we need to calculate the height of the layers.
- In HCP, the distance between adjacent layers can be represented using the tetrahedral arrangement. The height (h) of a tetrahedron formed by the atoms can be calculated.
- The height of the tetrahedron is given by the formula:
h=2√2r2√3
- The distance between the first and fifth layers involves four heights (since there are four layers between them).
- Therefore, the total height (H) between the first and fifth layers can be calculated as:
H=4h=4(2√2r2√3)
- Simplifying this gives:
H=8√2r2√3
- Thus, the shortest distance between the first and fifth layers of the HCP arrangement is:
H=8√2r√3
Topper's Solved these Questions
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercise -2 (Part-I)
19 Videos
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercise -2 (Part-II Single correct double value integer type)
9 Videos
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercise -1
20 Videos
- S BLOCK ELEMENTSBOOK - RESONANCE ENGLISHCHAPTER - S BLOCK ELEMENTSEXERCISE - ORGANIC CHEMISTRY(Biomolecules & Polymer)
4 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBOOK - RESONANCE ENGLISHCHAPTER - STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYEXERCISE - Section -B
18 Videos
Similar Questions
The shortest distance between two Na+ ions in rock - salt arrangement having edge length equal to a√2 picmeters is -
View SolutionWhat is the nearest distance between two different layers in ABAB arrangement (a=2× radius of the particle)
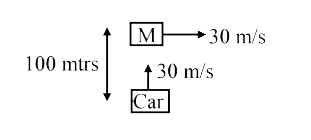
View SolutionThe shortest distance between the car and the motorcycle if their initial positions are as shown, will be :
View SolutionConsider two lines →r=ˆi+ˆj+λ1(ˆi−ˆk)and→r=ˆj+ˆk+λ2(ˆi+ˆj) . If PQ is the shortest distance between these two lines then: Their shortest distance is √26 Their point of intersection is ˆj+ˆk Their shortest distance is zero The length of projection of OPonˆi+ˆj+ˆkis2√3
View SolutionFind shortest distance between y2=4x and (x−6)2+y2=1
View SolutionKF crystallizes in the rock salt type structure. If the radius of K+ ion is 132 pm and that of F− ion is 135 pm.
(i)What is the shortest distance between K+ and F− ions ?
(ii)What is the edge length of the unit cell ?
(iii)What is closest K-K distance ?
View SolutionThe shortest distance between curves y2=8x and y2=4(x−3) is
View SolutionThe shortest distance between the line x=y and the curve y2=x−2 is
View SolutionThe shortest distance between a diagonal of a unit cube and the edge skew to it, is
View SolutionThe shortest distance between the point (0,12) and the curve x=√y,(y>0) , is:
View Solution
