A ball is thrown from a point with a speed 'v^(0)' at an elevation angle of θ . From the same point and at the same instant , a person starts running with a constant speed 'v0'2 to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection θ ?
No
Yes, 30∘
Yes, 60∘
Yes, 45∘
The correct Answer is:C
To solve the problem of whether the person can catch the ball and at what angle of projection, we can follow these steps:
Step 1: Understand the motion of the ball
The ball is thrown with an initial speed v0 at an angle θ. The horizontal and vertical components of the ball's velocity can be expressed as:
- Horizontal component: v0x=v0cosθ
- Vertical component: v0y=v0sinθ
Step 2: Analyze the motion of the person
The person starts running horizontally with a constant speed of v02.
Step 3: Determine the time of flight of the ball
The time of flight T of the ball can be calculated using the vertical motion. The ball will return to the ground when the vertical displacement is zero. The time of flight for projectile motion is given by:
T=2v0yg=2v0sinθg
where g is the acceleration due to gravity.
Step 4: Calculate the horizontal distance traveled by the ball
The horizontal distance R traveled by the ball when it lands can be calculated as:
R=v0x⋅T=(v0cosθ)⋅(2v0sinθg)=2v20sinθcosθg
Step 5: Calculate the distance covered by the person
The distance D covered by the person while the ball is in the air is:
D=speed⋅time=(v02)⋅T=(v02)⋅(2v0sinθg)=v20sinθg
Step 6: Set the distances equal for catching the ball
For the person to catch the ball, the horizontal distance traveled by the ball must equal the distance covered by the person:
2v20sinθcosθg=v20sinθg
Step 7: Simplify the equation
Cancelling v20sinθg from both sides (assuming v0≠0 and sinθ≠0):
2cosθ=1
cosθ=12
Step 8: Solve for θ
The angle θ that satisfies cosθ=12 is:
θ=60∘
Conclusion
Yes, the person will be able to catch the ball if the angle of projection θ is 60∘.
The ball is thrown with an initial speed v0 at an angle θ. The horizontal and vertical components of the ball's velocity can be expressed as:
- Horizontal component: v0x=v0cosθ
- Vertical component: v0y=v0sinθ
The person starts running horizontally with a constant speed of v02.
The time of flight T of the ball can be calculated using the vertical motion. The ball will return to the ground when the vertical displacement is zero. The time of flight for projectile motion is given by:
T=2v0yg=2v0sinθg
where g is the acceleration due to gravity.
The horizontal distance R traveled by the ball when it lands can be calculated as:
R=v0x⋅T=(v0cosθ)⋅(2v0sinθg)=2v20sinθcosθg
The distance D covered by the person while the ball is in the air is:
D=speed⋅time=(v02)⋅T=(v02)⋅(2v0sinθg)=v20sinθg
For the person to catch the ball, the horizontal distance traveled by the ball must equal the distance covered by the person:
2v20sinθcosθg=v20sinθg
Cancelling v20sinθg from both sides (assuming v0≠0 and sinθ≠0):
2cosθ=1
cosθ=12
The angle θ that satisfies cosθ=12 is:
θ=60∘
Yes, the person will be able to catch the ball if the angle of projection θ is 60∘.
Topper's Solved these Questions
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Advanced (Archive)
19 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - Level -1
140 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
Similar Questions
A boy throws a ball with a velocity u at an angle θ with the horizontal. At the same instant he starts running with uniform velocity to catch the ball before it hits the ground. To achieve this he should run with a velocity of
View SolutionA ball is fired from point P, with an initial speed of 50ms−1 at an angle of 53∘, with the horizontal. At the same time, a long wall ABat200m from point P starts moving toward P with a constant speed of 10ms−1. Find
(a) the time when the ball collides with wall AB.
(b) the coordinate of point C, where the ball xollides, taking point P as origin.
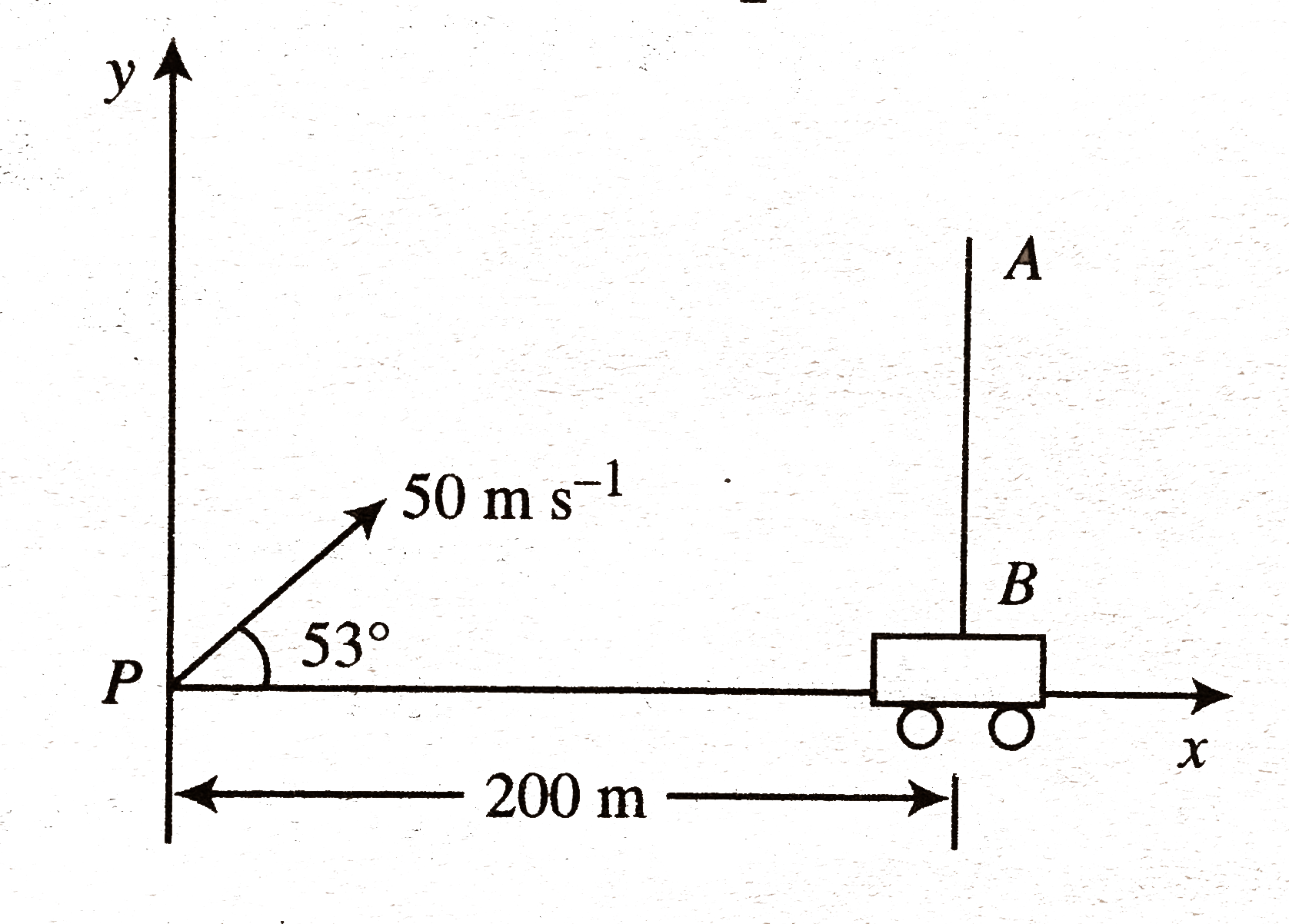 .
.
View Solution
Knowledge Check
A ball A is thrown up vertically with a speed u and at the same instant another ball B is released from a height h. At time t, the speed A relative to B is
AuBu - 2gtC√u2−2ghDu - gt
A ball is thrown onto a smooth floor with speed u at angle θ=45∘. If it rebounds with a speed v at the same angle ϕ=45∘. Then the coefficient of restitution is

View SolutionA ball is projected from top of the table with initial speed u at an angle of inclination θ, motion of image of ball w.r.t ball
View SolutionA ball is thrown downward In a viscous fluid with speed V. Terminal speed of ball is V0

View SolutionA projectile thrown with a speed v at an angle θ has a range R on the surface of earth. For same v and θ, its range on the surface of moon will be
View SolutionA ball is thrown horizontally from a point O with speed 20 m/s as shown. Ball strikes the incline along normal after two seconds
The speed of ball just before striking the plane is:

View SolutionA projectile is thrown with a speed v at an angle θ with the vertical. Its average velocity between the instants it crosses half the maximum height is
View SolutionA foot ball is kicked of with an inirial speed of 19.6 m/sec at a projection angle 45∘ . A receiver on the goal line 67.4 m away in the direction of the kick starts running to meet the ball at that in stant. What must his speed be if he is to catch the ball before it hits the ground?
View Solution
