If a body moving in circular path maintains constant speed of 10 , then which of the following correctly describes relation between acceleration and radius ?

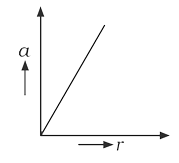
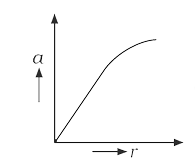

The correct Answer is:A
To solve the problem, we need to determine the relationship between acceleration and radius for a body moving in a circular path with a constant speed. Let's break it down step by step.
Step 1: Understand the types of acceleration in circular motion
In circular motion, there are two types of acceleration to consider:
1. Tangential Acceleration (a_t): This is related to the change in the speed of the object along the circular path. Since the speed is constant (10 m/s), the tangential acceleration is zero.
2. Centripetal Acceleration (a_c): This is the acceleration directed towards the center of the circular path, which keeps the object moving in a circle. It is given by the formula:
ac=v2r
where v is the constant speed and r is the radius of the circular path.
Step 2: Substitute the known values
Since the speed v is constant at 10 m/s, we can substitute this value into the centripetal acceleration formula:
ac=(10m/s)2r=100r
Step 3: Analyze the relationship between acceleration and radius
From the equation ac=100r, we can see that:
- As the radius r increases, the centripetal acceleration ac decreases.
- Conversely, as the radius r decreases, the centripetal acceleration ac increases.
This indicates that the centripetal acceleration is inversely proportional to the radius:
ac∝1r
Step 4: Graphical representation
The relationship ac∝1r suggests that if we plot acceleration on the y-axis and radius on the x-axis, the graph will be a hyperbola. Specifically, as r decreases, ac increases, and as r increases, ac decreases.
Conclusion
Thus, the correct description of the relationship between acceleration and radius for a body moving in a circular path with a constant speed of 10 m/s is that acceleration is inversely proportional to the radius, which can be represented graphically as a hyperbola.
Final Answer
The correct option that describes the relationship between acceleration and radius is Option A, which represents a hyperbola.
---
In circular motion, there are two types of acceleration to consider:
1. Tangential Acceleration (a_t): This is related to the change in the speed of the object along the circular path. Since the speed is constant (10 m/s), the tangential acceleration is zero.
2. Centripetal Acceleration (a_c): This is the acceleration directed towards the center of the circular path, which keeps the object moving in a circle. It is given by the formula:
ac=v2r
where v is the constant speed and r is the radius of the circular path.
Since the speed v is constant at 10 m/s, we can substitute this value into the centripetal acceleration formula:
ac=(10m/s)2r=100r
From the equation ac=100r, we can see that:
- As the radius r increases, the centripetal acceleration ac decreases.
- Conversely, as the radius r decreases, the centripetal acceleration ac increases.
ac∝1r
The relationship ac∝1r suggests that if we plot acceleration on the y-axis and radius on the x-axis, the graph will be a hyperbola. Specifically, as r decreases, ac increases, and as r increases, ac decreases.
Thus, the correct description of the relationship between acceleration and radius for a body moving in a circular path with a constant speed of 10 m/s is that acceleration is inversely proportional to the radius, which can be represented graphically as a hyperbola.
The correct option that describes the relationship between acceleration and radius is Option A, which represents a hyperbola.
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Level -1
Explore 140 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
A body is moving in a circular path with a constant speed. It has .
View SolutionA body is moving in a circular path with a constant speed. It has .
View SolutionAn object moving in a circular path at constant speed has constant
View SolutionIf a particle is moving on circular path with uniform speed,then which of the following physical quantity remains constant?
View Solutionfor a diatomic ideal gas in a closed system , which of the following plots does not correctly describe the relation between various thermodynamic quantities ?
View Solution(A) : If a body moving in a circular path with constant speed, then no force acts on it.
(R ) : The direction of the velocity vector of a body moving in a circular path is changing
View SolutionDoes a body moving around a circular path with constant speed have constant velocity? Give reasons.
View SolutionIf a body is moving with constant speed, then its acceleration
View SolutionA particle is moving on a circular path with constant speed, then its acceleration will be constant in
View SolutionA body of mass 100 g is rotating in a circular path of radius r with constant speed. The work done in one complete revolution is
View Solution