The initial speed of a bullet fired from a rifle is 630 m/s. . The rifle is fired at the centre of a target 700 m away at the same level as the target. How far above the centre of target, the rifle must be aimed in order to hit the target?
(a)6.1 m
(b)1.0 m
(c) 9.8 m
(d)4.2m
The correct Answer is:A
To solve the problem of how far above the center of the target the rifle must be aimed in order to hit the target, we can follow these steps:
Step 1: Understand the problem
We have a bullet fired from a rifle with an initial speed u=630m/s towards a target that is 700m away horizontally. We need to determine how high above the center of the target the rifle must be aimed to account for the bullet's drop due to gravity.
Step 2: Use the range formula for projectile motion
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where:
- R is the horizontal distance to the target (700 m),
- u is the initial speed (630 m/s),
- g is the acceleration due to gravity (approximately 10m/s2),
- θ is the angle of projection.
Step 3: Rearrange the formula to find sin(2θ)
Rearranging the formula gives:
sin(2θ)=R⋅gu2
Substituting the known values:
sin(2θ)=700⋅106302
Step 4: Calculate sin(2θ)
Calculating the right-hand side:
sin(2θ)=7000396900≈0.0176
Step 5: Find 2θ using the inverse sine function
Now, we can find 2θ:
2θ=sin−1(0.0176)
Calculating this gives:
2θ≈1.01∘
Thus,
θ≈0.505∘
Step 6: Calculate the time of flight
To find the time of flight t until the bullet reaches the target, we can use the horizontal motion:
t=Rucos(θ)
Using cos(0.505∘)≈0.9998:
t=700630⋅0.9998≈1.11s
Step 7: Calculate the vertical drop during time t
The vertical drop h due to gravity during time t is given by:
h=12gt2
Substituting the values:
h=12⋅10⋅(1.11)2≈6.17m
Step 8: Conclusion
The rifle must be aimed approximately 6.17m above the center of the target to hit it accurately.
We have a bullet fired from a rifle with an initial speed u=630m/s towards a target that is 700m away horizontally. We need to determine how high above the center of the target the rifle must be aimed to account for the bullet's drop due to gravity.
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where:
- R is the horizontal distance to the target (700 m),
- u is the initial speed (630 m/s),
- g is the acceleration due to gravity (approximately 10m/s2),
- θ is the angle of projection.
Rearranging the formula gives:
sin(2θ)=R⋅gu2
Substituting the known values:
sin(2θ)=700⋅106302
Calculating the right-hand side:
sin(2θ)=7000396900≈0.0176
Now, we can find 2θ:
2θ=sin−1(0.0176)
Calculating this gives:
2θ≈1.01∘
Thus,
θ≈0.505∘
To find the time of flight t until the bullet reaches the target, we can use the horizontal motion:
t=Rucos(θ)
Using cos(0.505∘)≈0.9998:
t=700630⋅0.9998≈1.11s
The vertical drop h due to gravity during time t is given by:
h=12gt2
Substituting the values:
h=12⋅10⋅(1.11)2≈6.17m
The rifle must be aimed approximately 6.17m above the center of the target to hit it accurately.
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Level -1
Explore 140 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
A bulley with muzzle velocity 100ms−1 is to be shot at a target 30m away in the same horizontal line. How high above the target must the rifle be aimed so that the bullet will hit the target ?
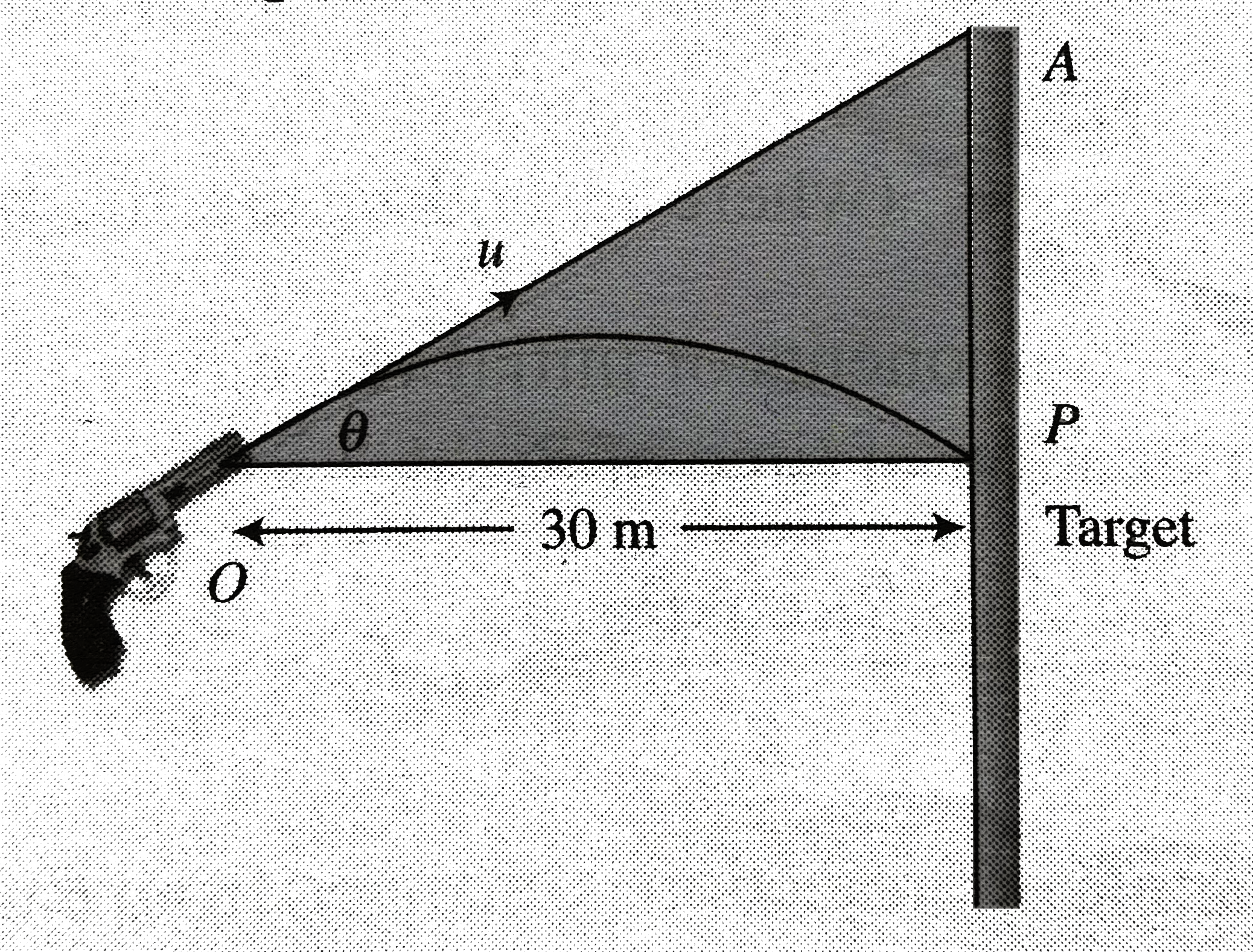 .
.
View SolutionA rifle shoots a bullet with a muzzle velocity of 400ms−1 at a small target 400m away. The height above the target at which the bullet must be aimed to hit the target is (g=10ms−2).
View Solution
Knowledge Check
A boy aims a gun at a bird from a point, at a horizontal distance of 100 m. If the gun can impart a velocity of 500 m/sec to the bullet, at what height above the bird must be aim his gun in order to hit it ?
A400 m/sB200 m/sC800 m/sD256 m/s
A rifle shoots a bullet with a muzzle velocity of 400ms−1 at a small target 400m away. The height above the target at which the bullet must be aimed to hit the target is (g=10ms−2).
View SolutionA gun fires a bullet at a speed of 140 ms−1. If the bullet is to hit a target at the same level as the gun and at 1km distance, the angle of projection may be
View SolutionA bullet of mass 20 g leaves a riffle at an initial speed 100 m/s and strikes a target at the same level with speed 50 m/s. The amount of work done by the resistance of air will be
View SolutionA bullet is to be fired with a speed of 2000m/s to hit a target 200m away on a level ground. If g=10m/s2, the gun should be aimed
View SolutionA bullet is fired from a gun eith a speed of 1000m/s on order to hit target 100 m away At what height above target should the gun be aimed ? (The resistance of air is negligible and g = 10 m/s2)
View SolutionA bullet moving with a velocity of 30√2ms−1 is fired into a fixed target. It penetrated into the target to the extent of s metres. If the same bullet is fired into a target of thickness s2 metres and of the same material with the same velocity, then the bullet comes out of the target with velocity
View SolutionThe probability of a man hitting a target is 1/2. How many times must he fire so that the probability of hitting the target at least once is more than 90%.
View Solution
