Assume that as narrow tunnel is dug between two diametrically opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that if a particle is released in this tunnel, it will execute a simple harmonic motion. Calculate the time period of this motion.
The correct Answer is:B
At centre of each force on particle is Zero. So it is the mean position.
At x distance from centre , force is to wards centre
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)40videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question56videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE2videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
Similar Questions
Consider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
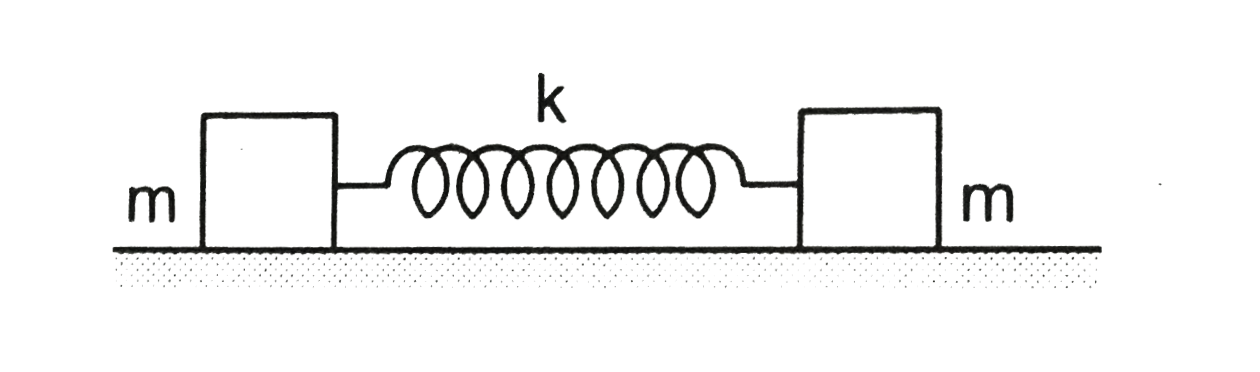 View Solution
View SolutionConsider the situation shown in figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2
Imagine a narrow tunnel between the two diametrically opposite points of the earth. A particle of mass m is released in this tunnel . The time period of oscillation is
View SolutionA cubical wood piece of mass 13.5 gm and volume 0.0027m3 float in water. It is depressed and released, then it executes simple harmonic motion. Calculate the period of oscillation ?
View SolutionAssume that a tunnel is dug through earth from North pole to south pole and that the earth is a non-rotating, uniform sphere of density ρ. The gravitational force on a particle of mass m dropped into the tunnel when it reaches a distance r from the centre of earth is
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal toView SolutionIf the earth was a homogeneous sphere and a straight hole was bored through its centre, show that a body dropped into this hole will execute shm. Calculate the time period if the radius of the earth is 6400 km and g = 9.8ms−2
View SolutionSuppose a vertical tunnel is dug along the diameter of earth , which is assumed to be a sphere of uniform mass density ρ. If a body of mass m is thrown in this tunnel, its acceleration at a distance y from the centre is given by
 View Solution
View SolutionSuppose a verticle tunnel is dug along the diametal of earth , which is assumed to be a sphere of unifrom mass density ρ. If a body of mass m is throws in this tunal, its acceleration at a distance y from the centre is given by
 View Solution
View Solution

