A body at the end of a spring executes SHM with a period t1, while the corresponding period for another spring is t2, If the period of oscillation with the two spring in series is T, then
T=t1+t2
T−2=T−21+T−22
T−1=T−11+T−12
T2=t21+t22
The correct Answer is:D
To solve the problem, we need to find the relationship between the time periods t1, t2, and T when two springs are connected in series.
1. Understanding the Time Period of a Spring:
The time period t of a spring executing simple harmonic motion (SHM) is given by the formula:
t=2π√mk
where m is the mass attached to the spring and k is the spring constant.
2. Expressing Time Periods for Individual Springs:
For the first spring with time period t1:
t1=2π√mk1
For the second spring with time period t2:
t2=2π√mk2
3. Finding the Effective Spring Constant for Springs in Series:
When two springs are connected in series, the effective spring constant kc can be found using:
1kc=1k1+1k2
This can be rearranged to:
kc=k1k2k1+k2
4. Finding the Time Period for the Springs in Series:
The time period T for the combined system of springs in series is:
T=2π√mkc
5. Substituting for kc:
Substitute kc into the equation for T:
T=2π
⎷mk1k2k1+k2=2π√m(k1+k2)k1k2
6. Relating T to t1 and t2:
Now, we can express T2 in terms of t21 and t22:
T2=4π2m(k1+k2)k1k2
From the expressions for t1 and t2:
t21=4π2mk1,t22=4π2mk2
Rearranging gives:
k1=4π2mt21,k2=4π2mt22
Substitute these into the equation for T2:
T2=(t21+t22)t21t22⋅4π2m
7. Final Relationship:
Thus, we can conclude that:
1T2=1t21+1t22
Conclusion:
The relationship between the time periods t1, t2, and T when two springs are in series is given by:
1T2=1t21+1t22
The time period t of a spring executing simple harmonic motion (SHM) is given by the formula:
t=2π√mk
where m is the mass attached to the spring and k is the spring constant.
For the first spring with time period t1:
t1=2π√mk1
For the second spring with time period t2:
t2=2π√mk2
When two springs are connected in series, the effective spring constant kc can be found using:
1kc=1k1+1k2
This can be rearranged to:
kc=k1k2k1+k2
The time period T for the combined system of springs in series is:
T=2π√mkc
Substitute kc into the equation for T:
T=2π
⎷mk1k2k1+k2=2π√m(k1+k2)k1k2
Now, we can express T2 in terms of t21 and t22:
T2=4π2m(k1+k2)k1k2
From the expressions for t1 and t2:
t21=4π2mk1,t22=4π2mk2
Rearranging gives:
k1=4π2mt21,k2=4π2mt22
Substitute these into the equation for T2:
T2=(t21+t22)t21t22⋅4π2m
Thus, we can conclude that:
1T2=1t21+1t22
The relationship between the time periods t1, t2, and T when two springs are in series is given by:
1T2=1t21+1t22
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL (2)
Explore 40 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:IN-CHAPTER EXERCISE F
Explore 10 Videos
Similar Questions
A mass is suspended at the end of a spring and performs SHM with a time period 3 seconds, while the time period f same mass wih other spring is 4 second. If that mass is connected with the combination of the two springs connected in series then time period of oscillator is
View SolutionThe time period of oscillations of a block attached to a spring is t1. When the spring is replaced by another spring, the time period of the block is t2. If both the springs are connected in series and the block is made to oscillate using the combination, then the time period of the block is
View Solution
Knowledge Check
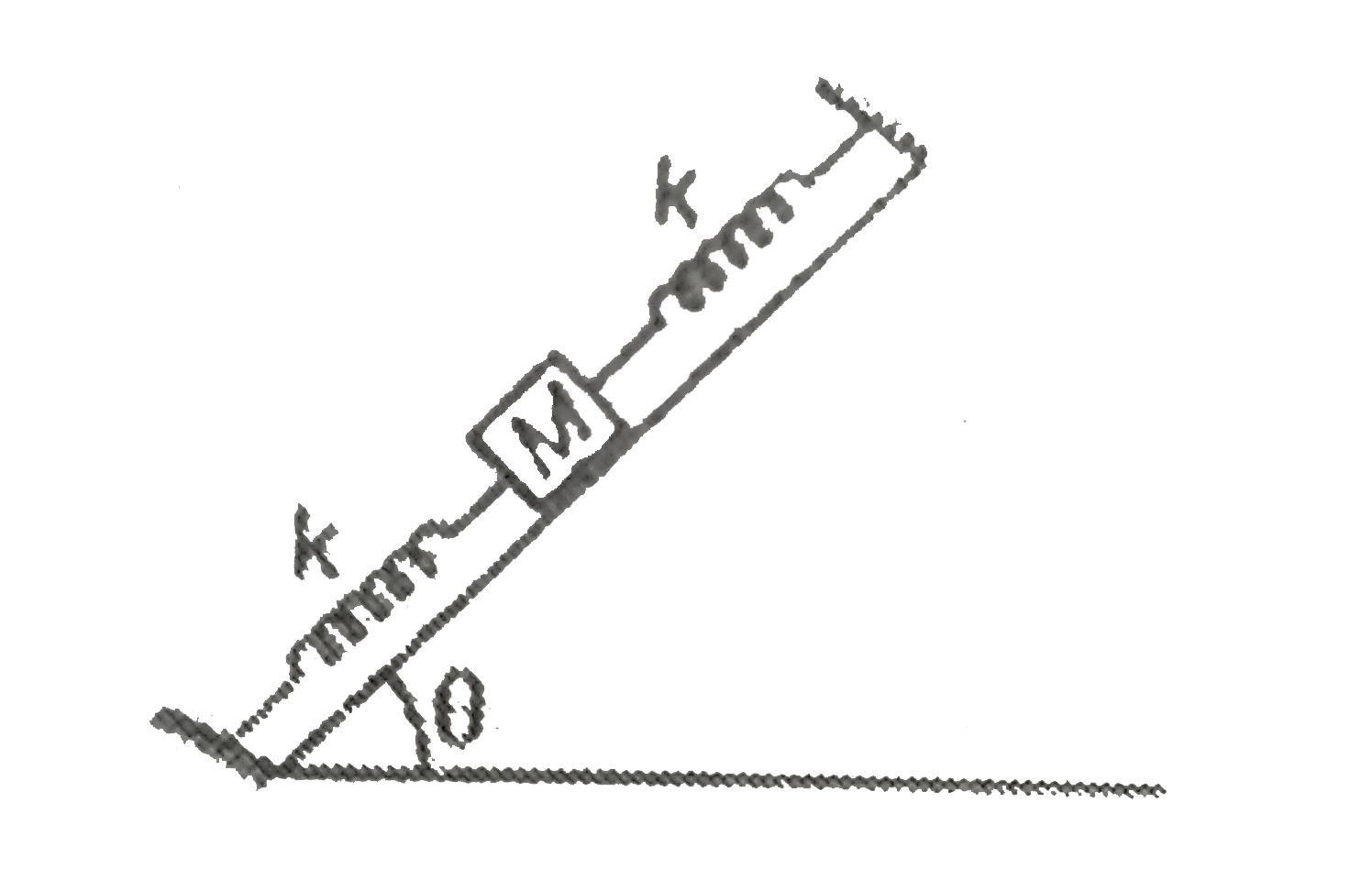
On a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
 A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
In the adjacent figure, if the incline plane is smooth and the springs are identical then the period of oscillation of this body is

View SolutionWhen a boy is playing on a swing in the sitting position , the time period of oscillations of the swing is T. If the boy stands up , the time period of oscillation of the spring will be
View SolutionTime period of a given spring-mass system is

View SolutionA body is in SHM with period T when oscillated from a freely suspended spring. If this spring is cut in two parts of length ratio 1:3& again oscillated from the two the two parts separatedly, then the periods are T1&T2 then find T1/T2.
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
View SolutionA body of mass m hung at one end of the spring executes simple harmonic motion . The force constant of a spring is k while its period of vibration is T. Prove by dimensional method that the equation T=2π√m/k is correct. Dervive the correct equation , assuming that they are related by a power law.
View SolutionIf the period of oscillation of mass M suspended from a spring is one second, then the period of 9M will be
View Solution