Two springs of force constants k1 and k2, are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
_E01_383_Q01.png)
f/4
(b)4f
(c)2f
(d)f/2
The correct Answer is:C
Here, K1and k2 are in parallel, so k=k1+k2 The frequency K1 and K2 are made four times their original values,
K'=4K1+4K2=4K2=4(k1+k2)
So the new frequency of oscillation is f'=12π√4k1+k2m ∴ f'/f=√4=2⇒f'=2f
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)40videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
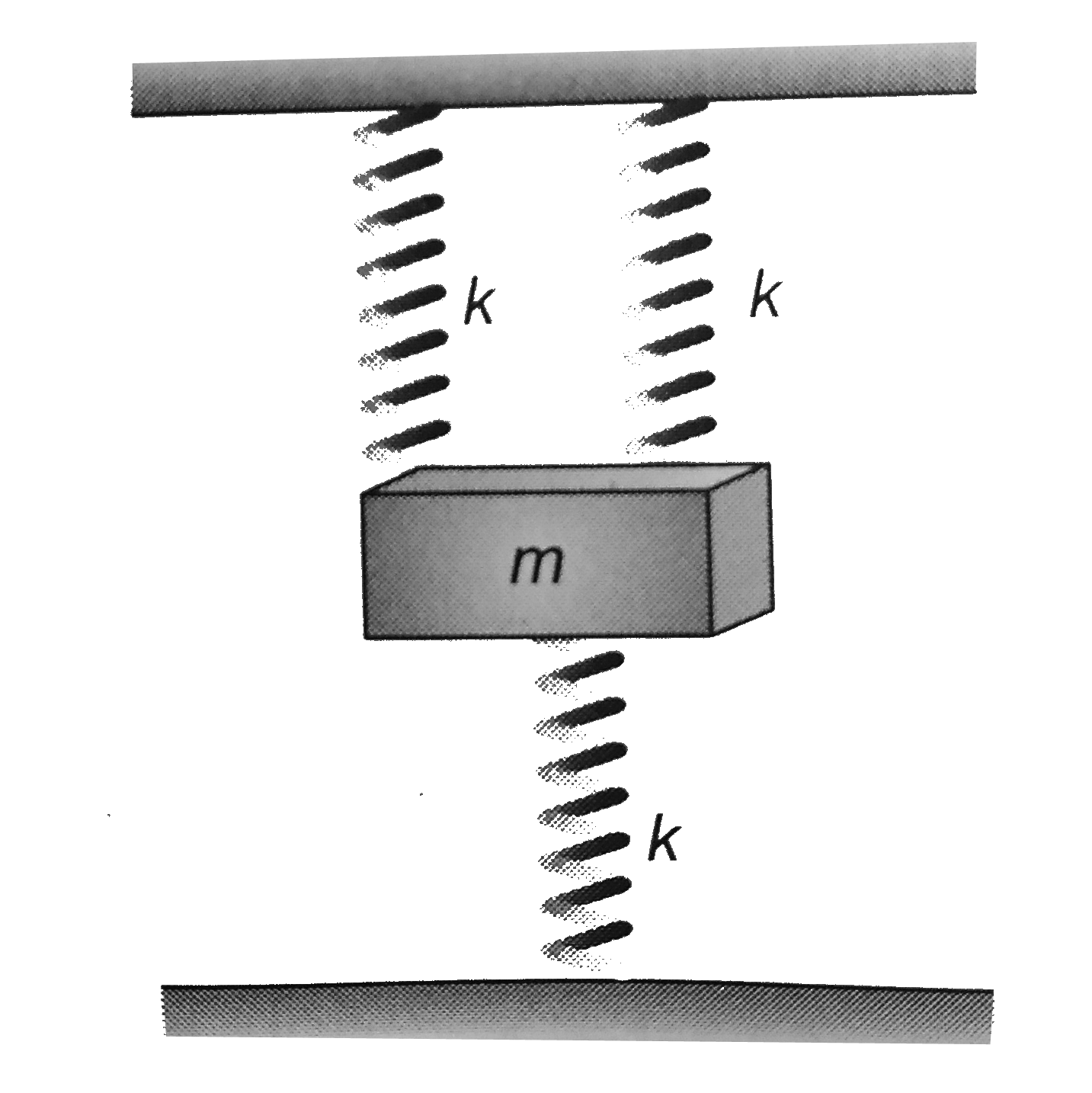
View SolutionIn the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
 View Solution
View SolutionTwo springs have their force constant as k1 and k2(k1>k2). When they are streched by the same force.
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
 View Solution
View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is
 View Solution
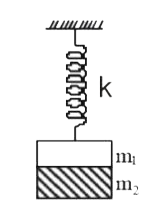
View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant K. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is -
 View Solution
View Solution

