A particle is executing simple harmonic motion with a time period. T. At time t=0, it is at its position of equilibrium. The kinetic energy -time graph of the particle will look like:
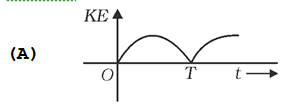
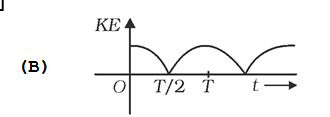
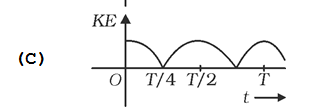
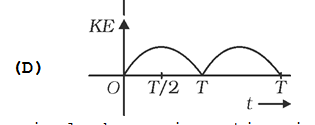
The correct Answer is:C
KE is maximum at mean position and minimum at extreme position (at )
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)
40 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
A particle is executing simple harmonic motion with a time period T. At time t=0, it is at its position of equilibium. The kinetice energy -time graph of the particle will look like
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View Solution
Knowledge Check
A particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2A particle is executing simple harmonic motion. Its total energy is proportional to its
Adisplacement from equilibrium positionBfrequency of oscillationCsquare of amplitude of motionDvelocity at equilibrium positionA particle executing simple harmonic motion with an amplitude A. The distance travelled by the particle in one time period is
AzeroBAC2AD4A
For a particle executing simple harmonic motion, the acceleration is proportional to
View SolutionWhile a particle executes linear simple harmonic motion
View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View SolutionThe displacement of a particle in simple harmonic motion in one time period is
View SolutionA particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View Solution
