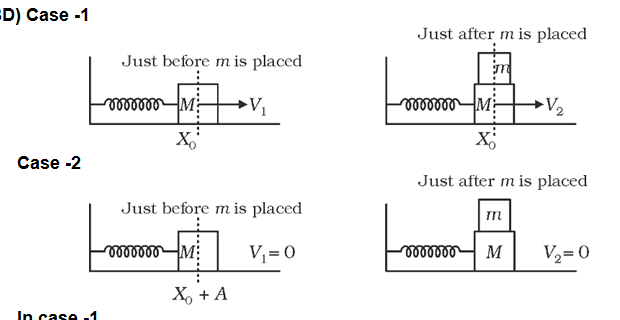
A disc is free to rotate about a smooth horizontal axis passing through its centre of mass. A particle is fixed at the top of the disc. A slight push is given to the disc and it starts rotating. During the process.

The amplitude of oscillation in the first case changes by a factor of √mm+M, whereas in the second case it remains unchanged
The final time period of oscillation in both the cases is same
The total energy decreases in both the cases
The instantaneous speed at x0 of the combined masses decreases in both the cases
The correct Answer is:ABD
In case-1,
Mv1=(M+m)v2, v2=(MM+m)v1
√KM+mA2=(MM+m)√KMA1, A2=√MM+mA1
In case -2
A2=A1, T=2π√M+mK in both cases.
Total energy decreases in first case whereas remain same in 2nd case. Instantaneous speed at x0 decreases in both cases.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question56videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
Similar Questions
A thin horizontal circular disc is roating about a vertical axis passing through its centre. An insect is at rest at a point near the rim of the disc. The insect now moves along a diameter of the disc to reach its other end. During the journey of the insect, the angular speed of the disc.
View SolutionTwo men each of mass m stand on the rim of a horizontal circular disc, diametrically opposite to each other. The disc has a mass M and is free to rotate about a vertical axis passing through its centre of mass. Each mass start simultaneously along the rim clockwise and reaches their original starting positions on the disc. The angle turned through by disc with respect to the ground (in radian) is
View SolutionA charge q is uniformly distributed along the periphery of a non conducting uniform circular disc pivoted at its centre in a vertical plane and can freely rotate about a horizontal axis passing through its centre. A cylindrical region with its axis passing through the centre of the disc has a varying magnetic field B = kt as shown in the adjacent figure. wrapped over the disc as shown and remains stationary, then
View SolutionA uniform disc is rotating at a constantt speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upward. Then about the fixed axis, the angular speed of the
View SolutionAn uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upwards, then about the fixed axis.
STATEMENT-1 : Angular speed of the disc about the aixs of rotation will increase.
and
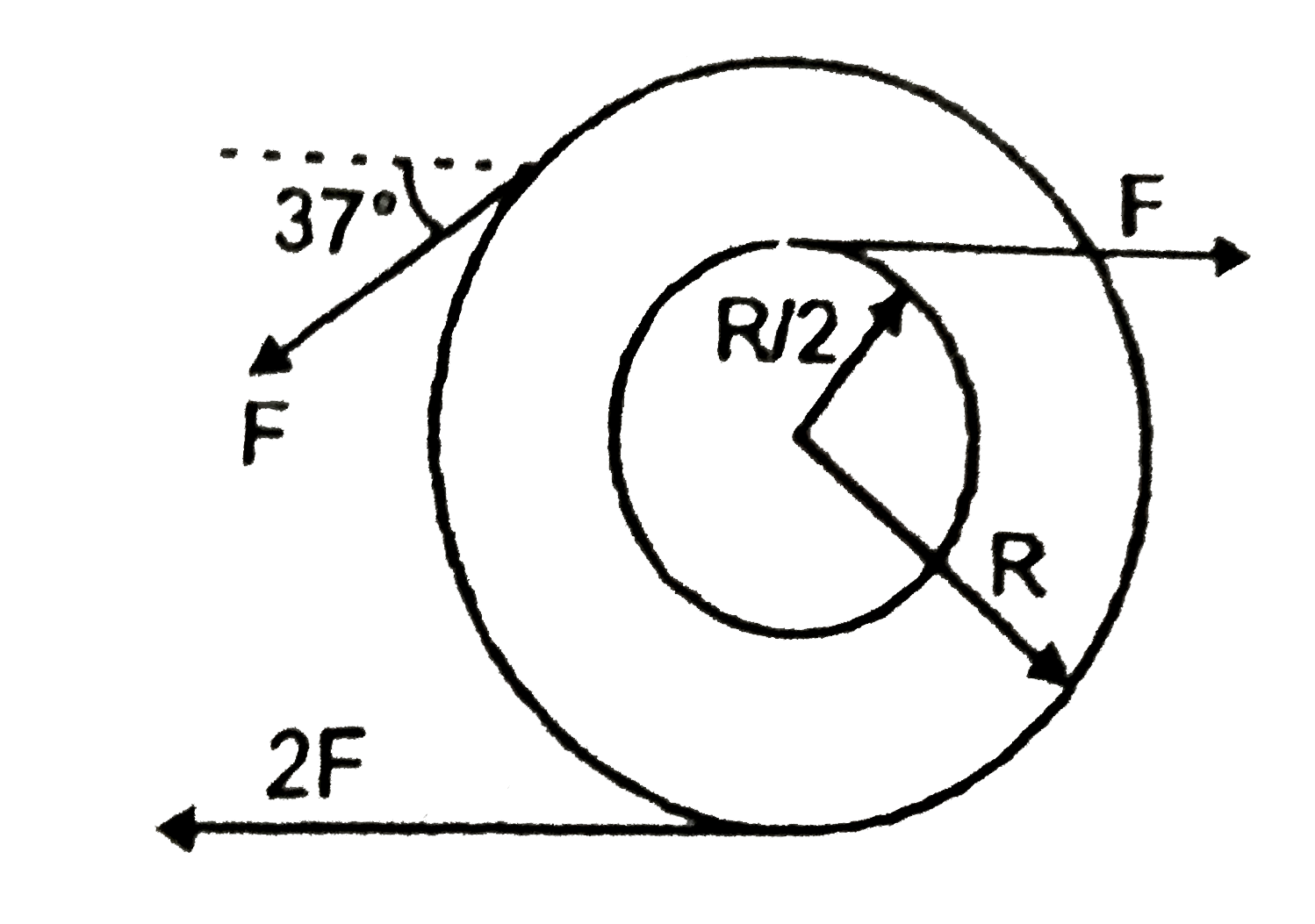
STATEMENT-2 : Moment of inertia of the disc is decreased about the axis of rotation.View SolutionOn a disc of radius R a concentric circle of radius R/2 is drawn. The disc is free to rotate about a frictionless fixed axis through its center and perpendicular to plane of the disc. All three forces ( in plane of the disc ) shown in figure are exerted tangent to their respective circular periphery. The magnitude of the net torque ( about centre of disc ) acting on the disc is :
 View Solution
View SolutionOn a disc of radius R a concentric circle of radius R/2 is drawn. The disc is free to rotate about a frictionless fixed axis through its center and perpendicular to plane of the disc. All three forces ( in plane of the disc ) shown in figure are exerted tangent to their respective circular periphery. The magnitude of the net torque ( about centre of disc ) acting on the disc is :
 View Solution
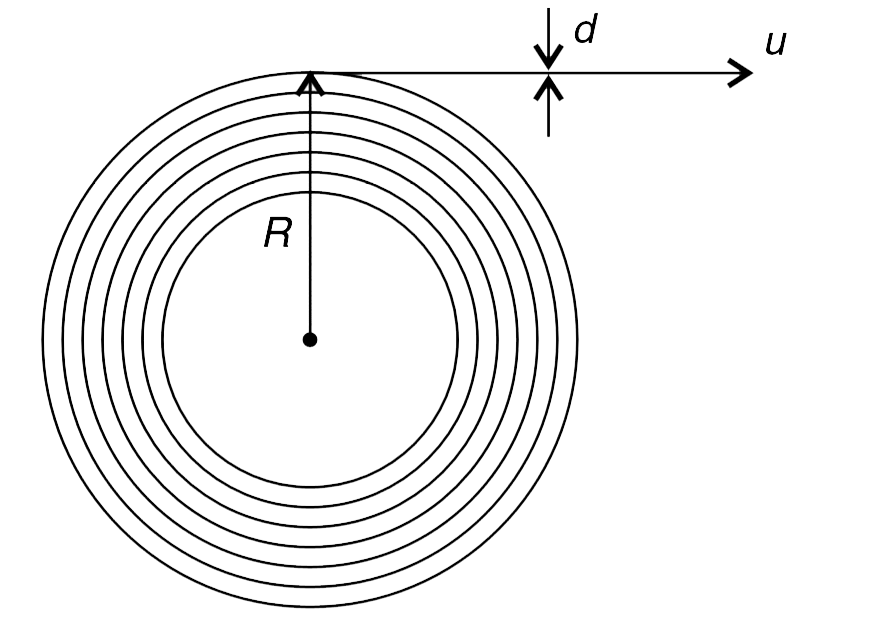
View SolutionA disc is free to rotate about an axis passing through its centre and perpendicular to its plane. The moment of inertia of the disc about its rotation axis is I. A light ribbon is tightly wrapped over it in multiple layers. The end of the ribbon is pulled out at a constant speed of u. Let the radius of the ribboned disc be R at any time and thickness of the ribbon be d(<<R). Find the force (F) required to pull the ribbon as a function of radius R.
 View Solution
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane about a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddenly attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc isView Solution

