Blocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
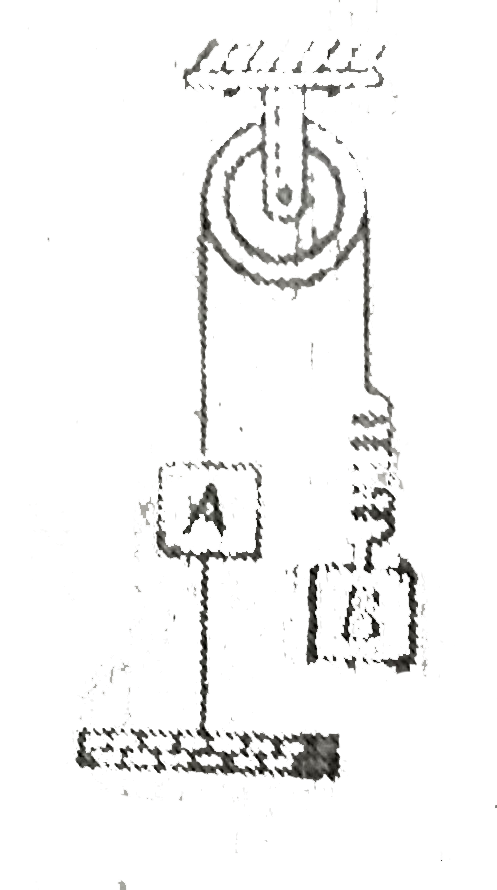
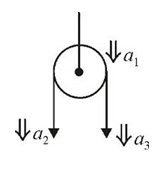
a2−a1=a1−a2
At an extension of x04of the spring, the magnitude of acceleration of the block connected to the spring is 3g10
x0=4Mgk
When spring achieves an extension of x02 for the first time, the speed of the block connected to the spring is 3g(M)5K
The correct Answer is:A
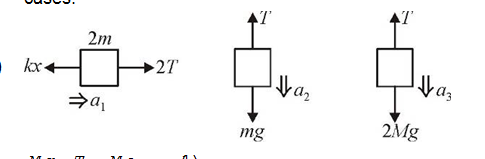
Mg−T=Ma2 ...(1)
2Mg−T=3Ma3 ...(2)
2T−Kx=2Ma1 ...(3)
From (1) and
M(a2+a3)=Mg-T+Mg−T2=2Mg−3T2∣∣∣
implies 2Ma1=2Mg−3T2×43⇒8Ma13=3Ma3=3Ma3−2T ...(4)
(3)+(4)⇒8Mg3−kx=(2M+8M3)a1
⇒14M3a1=−K[x−8Mg3K]⇒a1=−3K14M[x−8Mg3K]
ω=√3K14M,A=8Mg3Kx02=2A[Maximum elongation=2A]
Vmax=Aω=8Mg3K√3K14M a1atx=x04=−3K14M×(4Mg)(3K)=2g7 Correct answer is (A)
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question56videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
Similar Questions
In the adjoining figure, block A is of mass (m) and block B is of mass 2m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched. Find the maximum extension in the spring and acceleration of block B at time of maximum extension
 .View Solution
.View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
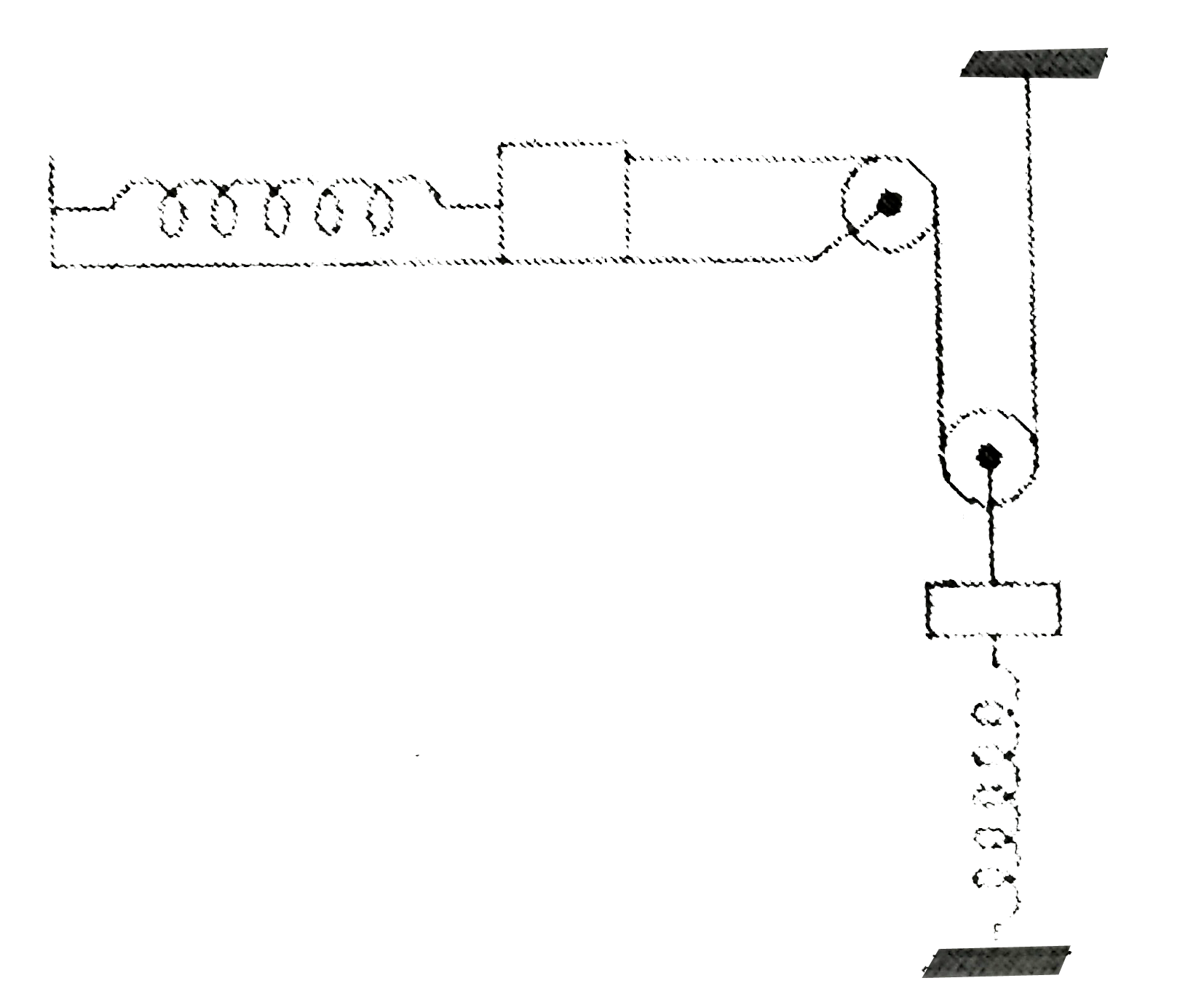
In the equilibrium position, speed of the block placed horizontally isView SolutionThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
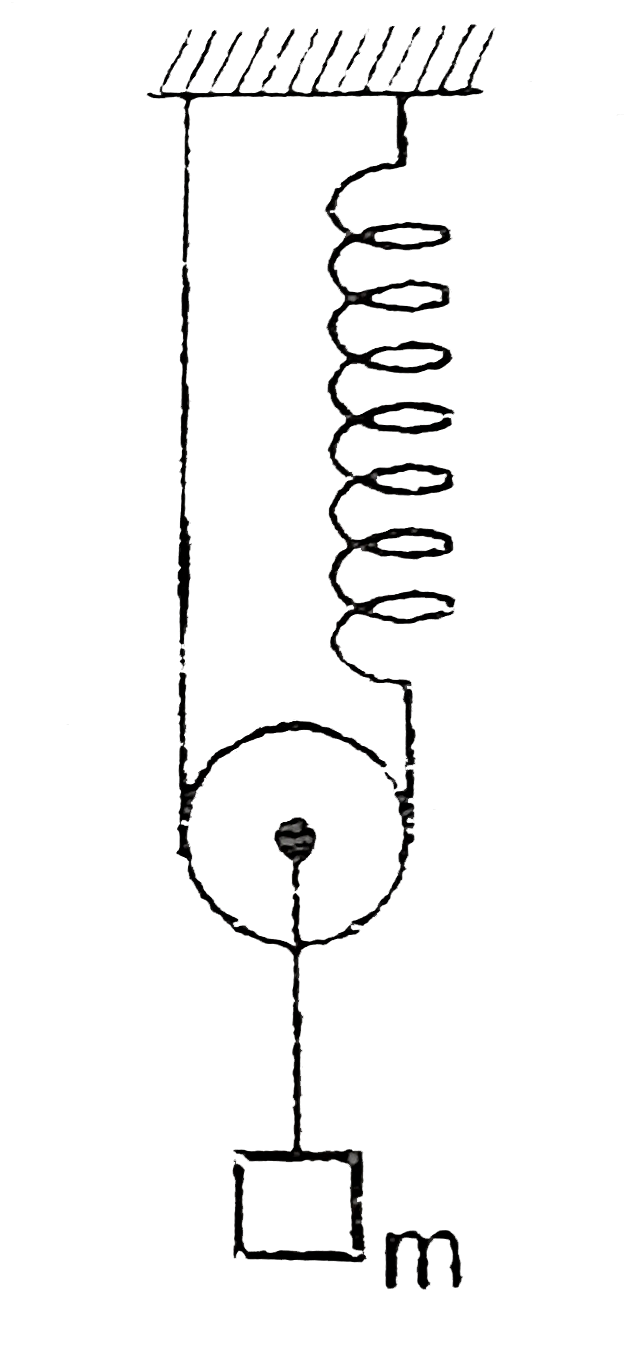 View Solution
View SolutionConsider the situation shown in figure.
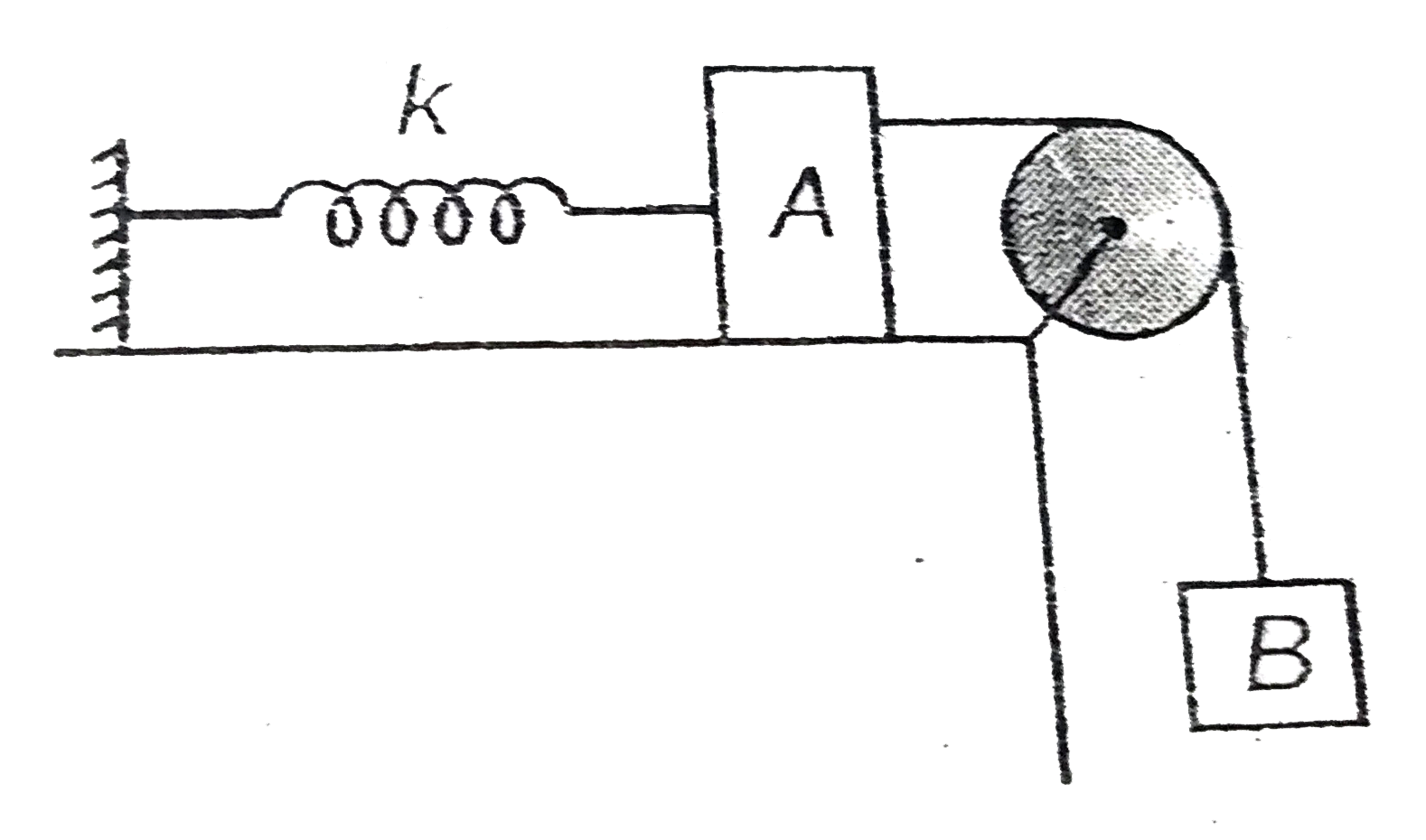
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
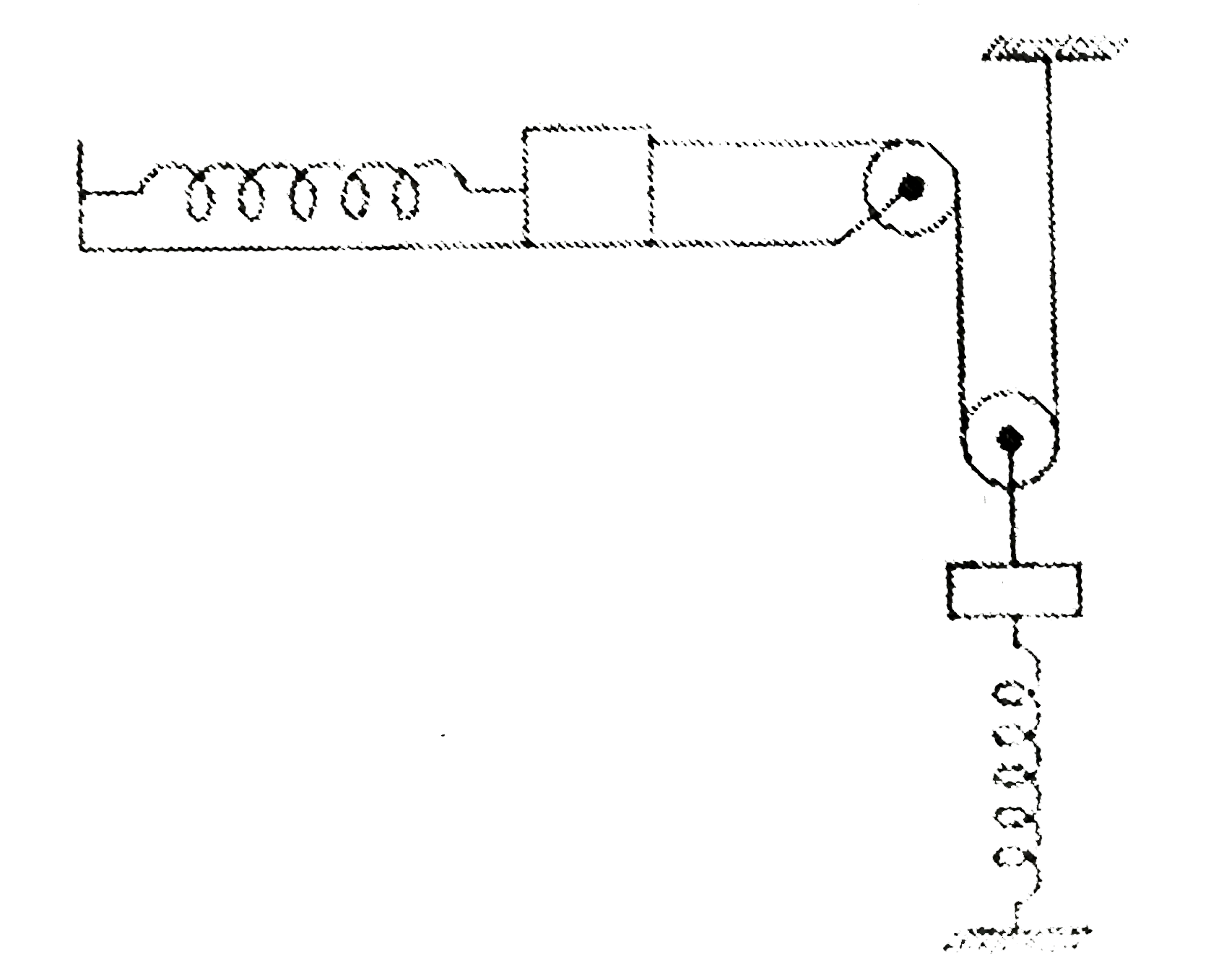
Extension of horizontal spring in equilibrium isView SolutionConsider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the puley, find the maximum eleongation of the spring.
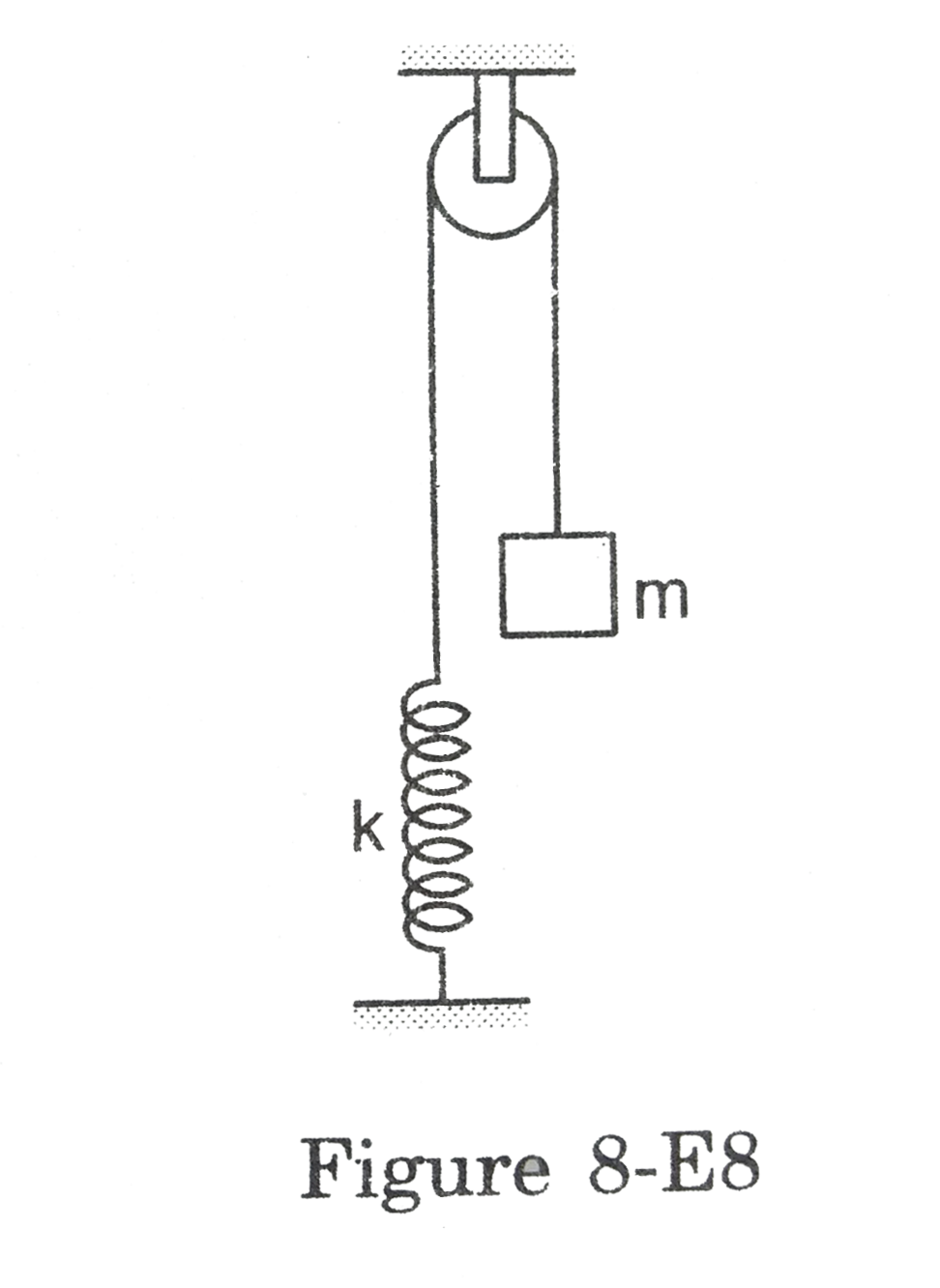 View Solution
View SolutionIn a vertical spring mass system, a block of mass m is initially at rest when there is no extension. Now if the mass is released suddenly, then the maximum elongation in the spring is
View Solution

