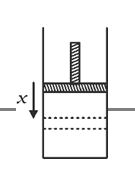
An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass M. The piston and cylinder have equal cross sectional area A. When the piston is in equilibrium, the volume of the gas is and its pressure is The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency:
The correct Answer is:
In equilibrium pressure inside the cylinder = pressure just outside it
or
When piston is displaced slightly by an amount x, change in volume,
Since, the cylinder is isolated from the surroundings, process is adiabatic in nature. In adiabatic process,
or increase in pressure inside the cylinder,
This increase in pressure when multiplied with area of cross-section A will give a net upward force (or the restoring force). Hence,
or
Since, motion of the piston is simple harmonic in nature. Frequency of this oscillation is given by
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View Solution
Knowledge Check
An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
A12π√MV0AγP0B12πAγP0V0MC12πV0MP0A2γD12π√A2γP0MV0
A cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA smooth piston of mass m area of cross - section A is in equilibrium in a gas jar when the pressure of the gas is P0. Find the angular frequency of oscillation of the piston, assuming adiabatic Change of state of the gas.

View SolutionAn ideal gas enclosed in a cylinder fitted with a frictionless and weightless piston, pushes it outside. What would be the sign convention for the work ?
View SolutionAn ideal gas enclosed in a cylinder fitted with a frictionless and weightless piston, pushes it outside. What would be the sign convention for the work ?
View SolutionAn ideal monoatomic gas is enclosed in a fixed horizontal adiabatic cylinder of cross sectional area A. The cylinder is fitted with an adiabatic piston of mass m (attached to one end of a spring as shown) which can move horizontally without friction inside the cylinder. In equilibrium, the spring is in natural length and pressure and volume are P0 and V0 respectively. The piston is slightly displaced from equilibrium and released. Then, frequency of small oscillation is

View SolutionA gas is contained in a metallic cylinder fitted with a piston.the piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
View SolutionA gas is contained in a metallic cylinder fitted with a piston.The piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
View Solution
