A particle moving in a straight line has velocity-displacement equation as v=5√1+s. Here v is in ms−1 and s in metres. Select the correct alternative.
Particle is initially at rest.
Initial velocity of the particle is 5 m/s and the particle has a constant acceleration of 12.5ms−2
Particle moves with a uniform velocity
Acceleration of the particle increase linearly with time
The correct Answer is:B
v=5√1+s⇒v2=25(t+s) Taking derivative wrts
2vdvds=25⇒a=VdVds=12.5m/s2
V=5 When s= 0 ⇒ Initial velocity is m/s
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 2
65 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)
19 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionA particle moves along a straight line and its velocity depends on time as v=3t−t2. Here, v is in m/s and t in second. Find
(a) average velocity and
(b) average speed for first five seconds.
View SolutionDisplacement time graph of a particle moving in a straight line is as shown in figure. Select the correct alternative (s) :
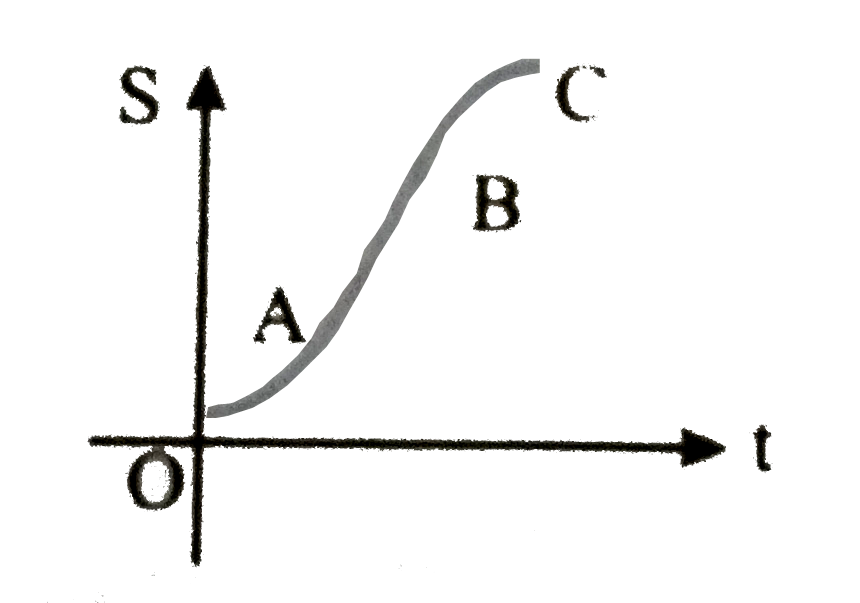 .
.
View SolutionA particle moving in a straight line has its velocit varying with time according to relation v=t2−6t+8(m/s) where t is in seconds. The CORRECT statement(s) about motion of this particle is/are:-
View SolutionThe speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v2=144−9x2. Select the correct alternatives
View SolutionThe speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v2=144−9x2. Select the correct alternatives
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (s) as a=2s. The velocity of the particle is zero at zero displacement. Find the corresponding velocity-displacement equation.
View Solution
