At t=0 and x=0 , an initially stationary blue car begins to accelerate at a constant rate of 2.0m/s2 in the positive direction of the x -axis At =t = 2s a red car travelling in an adjecent lane and in the same direction passes x =0 with a speed of 8.0m/s and a constant accleration of 3.0m/s2 .the time when red car passes the blue car is :
(a)4.2 s
(b)3.6 s
(c)2.9 s
(d)None of these
The correct Answer is:C
To solve the problem of when the red car passes the blue car, we can break it down into a series of steps:
1. Define the Motion of the Blue Car:
- The blue car starts from rest (initial velocity uB=0) and accelerates at a constant rate aB=2.0m/s2.
- The position of the blue car as a function of time t can be described by the equation of motion:
xB=uBt+12aBt2
- Substituting the values:
xB=0+12⋅2⋅t2=t2
2. Define the Motion of the Red Car:
- The red car passes x=0 at t=2s with an initial speed uR=8.0m/s and accelerates at aR=3.0m/s2.
- The position of the red car as a function of time t (considering it starts moving at t=2s) is given by:
xR=uR(t−2)+12aR(t−2)2
- Substituting the values:
xR=8(t−2)+12⋅3(t−2)2
- Simplifying this:
xR=8t−16+32(t2−4t+4)
xR=8t−16+32t2−6t+6
xR=32t2+2t−10
3. Set the Positions Equal to Find When They Meet:
- To find the time when the red car passes the blue car, set xB=xR:
t2=32t2+2t−10
- Rearranging gives:
0=32t2−t2+2t−10
0=12t2+2t−10
0=t2+4t−20
4. Solve the Quadratic Equation:
- Using the quadratic formula t=−b±√b2−4ac2a:
- Here, a=1, b=4, and c=−20.
t=−4±√42−4⋅1⋅(−20)2⋅1
t=−4±√16+802
t=−4±√962
t=−4±4√62
t=−2±2√6
5. Select the Positive Root:
- Since time cannot be negative, we take:
t=−2+2√6
- Approximating √6≈2.45:
t≈−2+4.9≈2.9s
Final Answer:
The time when the red car passes the blue car is approximately t≈2.9s.
- The blue car starts from rest (initial velocity uB=0) and accelerates at a constant rate aB=2.0m/s2.
- The position of the blue car as a function of time t can be described by the equation of motion:
xB=uBt+12aBt2
- Substituting the values:
xB=0+12⋅2⋅t2=t2
- The red car passes x=0 at t=2s with an initial speed uR=8.0m/s and accelerates at aR=3.0m/s2.
- The position of the red car as a function of time t (considering it starts moving at t=2s) is given by:
xR=uR(t−2)+12aR(t−2)2
- Substituting the values:
xR=8(t−2)+12⋅3(t−2)2
- Simplifying this:
xR=8t−16+32(t2−4t+4)
xR=8t−16+32t2−6t+6
xR=32t2+2t−10
- To find the time when the red car passes the blue car, set xB=xR:
t2=32t2+2t−10
- Rearranging gives:
0=32t2−t2+2t−10
0=12t2+2t−10
0=t2+4t−20
- Using the quadratic formula t=−b±√b2−4ac2a:
- Here, a=1, b=4, and c=−20.
t=−4±√42−4⋅1⋅(−20)2⋅1
t=−4±√16+802
t=−4±√962
t=−4±4√62
t=−2±2√6
- Since time cannot be negative, we take:
t=−2+2√6
- Approximating √6≈2.45:
t≈−2+4.9≈2.9s
The time when the red car passes the blue car is approximately t≈2.9s.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)19videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)14videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 175videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)1videos
JEE MAIN REVISON TEST-23
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
Similar Questions
A car that's initially traveling at 10m/s accelerates uniformly for 4 seconds at a rate of 2m/s2 in a straight line. How far does the car travel during this time ?
View SolutionA motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0m/s2 for 8.0s. How far does the boat travel during this time ?
View SolutionTwo cars A and B are at rest at same point initially. If A starts with uniform velocity of 40 m/sec and B starts in the same direction with constant acceleration of4m/s2,then B will catch A after :
View SolutionA car moving on a straight road accelerates from a speed of 4.1 m/s to a speed of 6.9 m/s in 5.0 s. What was its average acceleration?
View SolutionA car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
View SolutionThe brakes applied to a car produce an acceleration of 6m/s2 in the opposite direction to the motion . If the car takes 2s to stop after the application of brakes , calculate the distance it travels during this time.
View SolutionA particle starts from the origin at t = 0 s with a velocity of 10.0ˆj m/s and moves in plane with a constant acceleration of (8ˆi+2ˆj)ms−2. The y-coordinate of the particle in 2 sec is
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
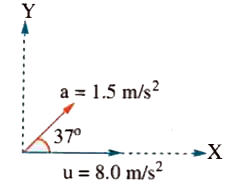
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.View SolutionA car is travelling at 20 m/s on a circular road of radius 100 m. It is increasing its speed at the rate of 3 m/s2. Its acceleration is
View SolutionTwo cars get closer by 8 m every second while traveling in the opposite directions. They get closer by 0.8 m while traveling in the same directions. What are the speeds of the two cars ?
View Solution

