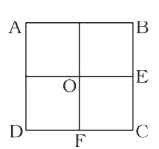
A square of side 4 cm and of uniform thickness is divided into four equal squares. If one of them is cut off (OECF), then the position of the centre of mass of the remaining portion from O is . Find the value of K.
The correct Answer is:3
Let be surface mass density. The mass of the removed portion may be taken as negative. The given system may be regarded as two-particle system—one particle of mass at (0, 0) and second particle of mass at (1 , -1).
Now,
.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - Level - 1 PARAGRAPH QUESTIONS3videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 248videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 0 - LONG ANSWER TYPE5videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
A square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is
 View Solution
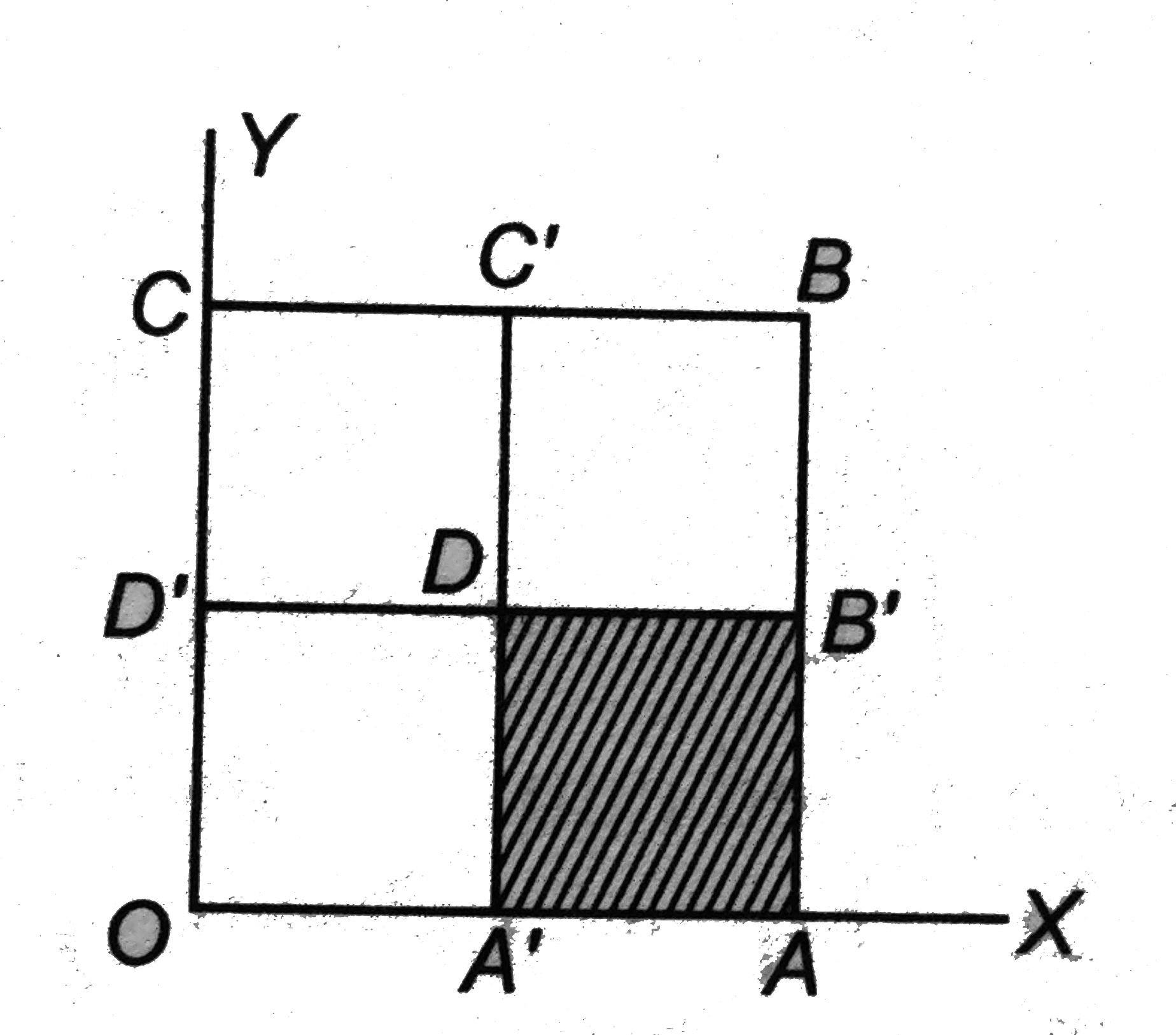
View SolutionA square of side 4cm and uniform thickness is divided into four squares. The square portion A′AB′D is removed and the removed portion is placed over the portion DB′BC′. The new position of centre of mass is
 View Solution
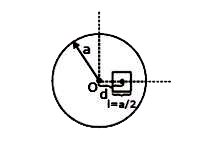
View SolutionA square shaped hole of side l=a2 is carved out at a distance d=a2 from the centre 'O' of a uniform circular disk of radius a. If the distance of the centre of mass of the remaining portion from O is −ax value of X (to the nearest integer) is _________.
 View Solution
View SolutionA circular plate of uniform thickness has a diameter fo 56cm. A circular portion of diameter 42 cm is removed from one edge of the plate as shown in figure. Find the position of the centre of mass of the remaining portion.
 View Solution
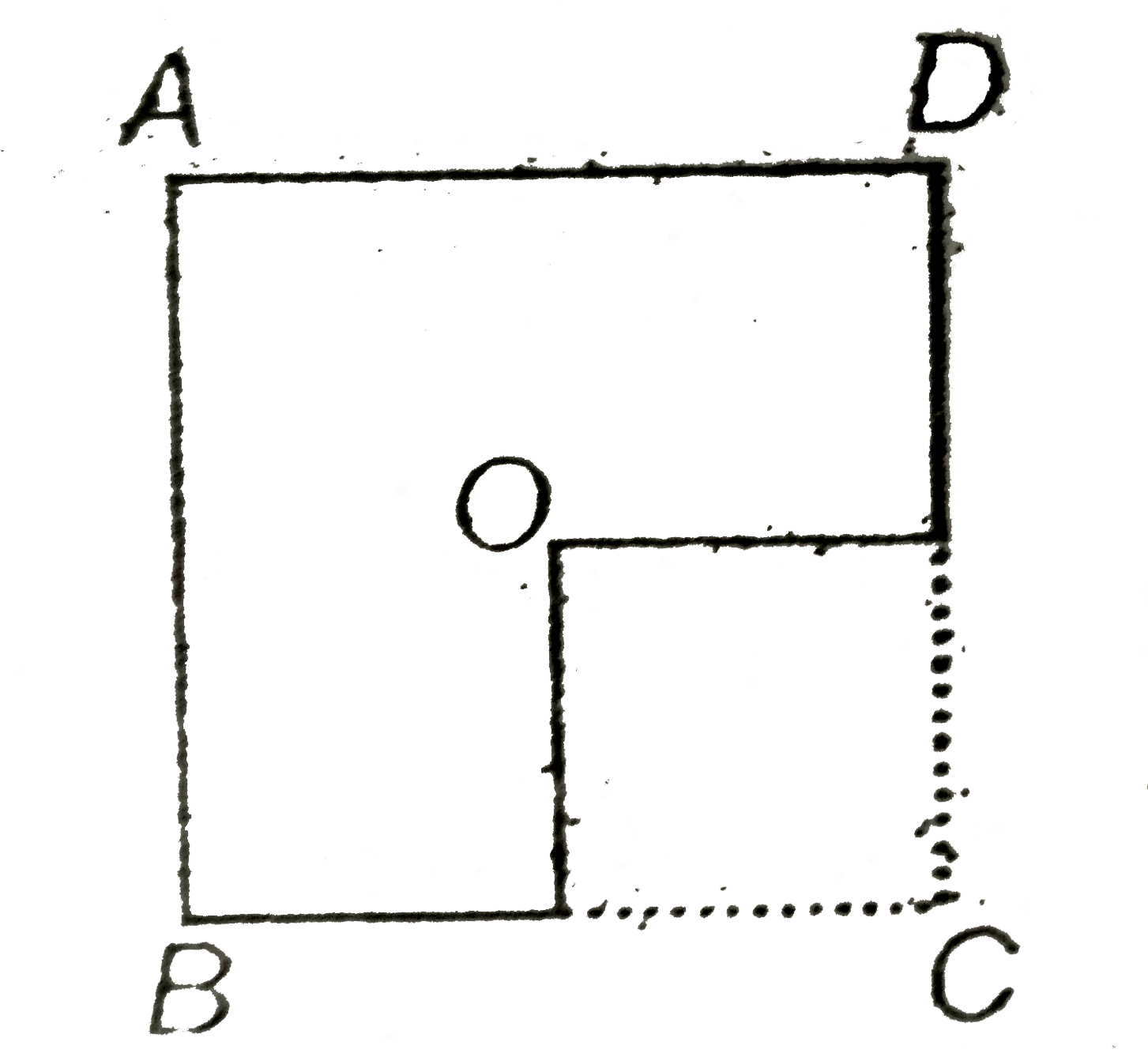
View SolutionFrom a uniform square plate, one-fourth part is removed as shown. The centre of mass of remaining part will lie on
 View Solution
View SolutionFrom a uniform square plate, one-fourth part is removed as shown. The centre of mass of remaining part will lie on
 View Solution
View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :
 View Solution
View SolutionA square of side a2 is removed from a disc having radius a . Find centre of mass of remaing portion.
 View Solution
View SolutionFour holes of radius R are cut from a thin square plate of side 4R and mass M. The moment of inertia of the remaining portion about z-axis is :
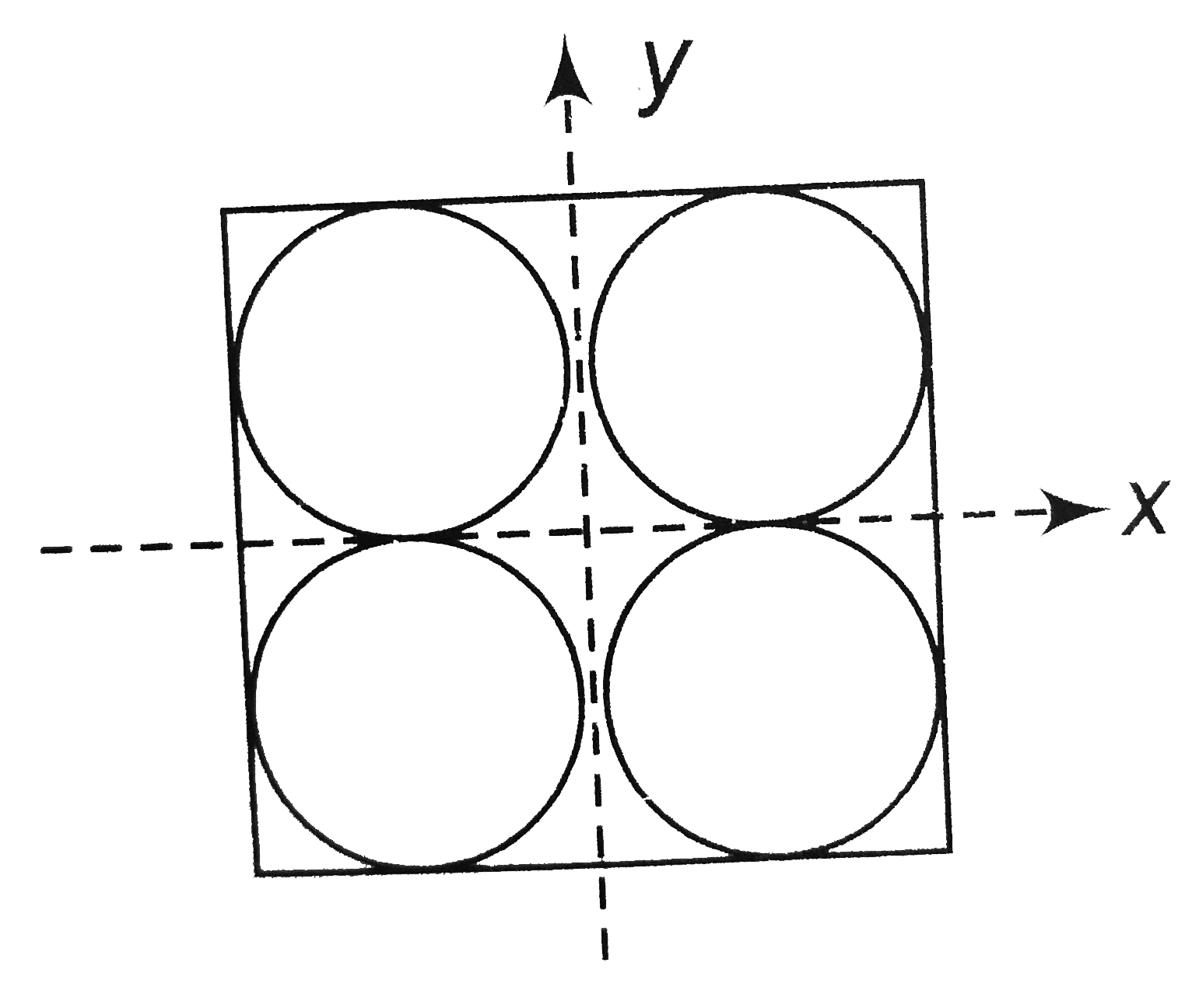 .View Solution
.View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View Solution

