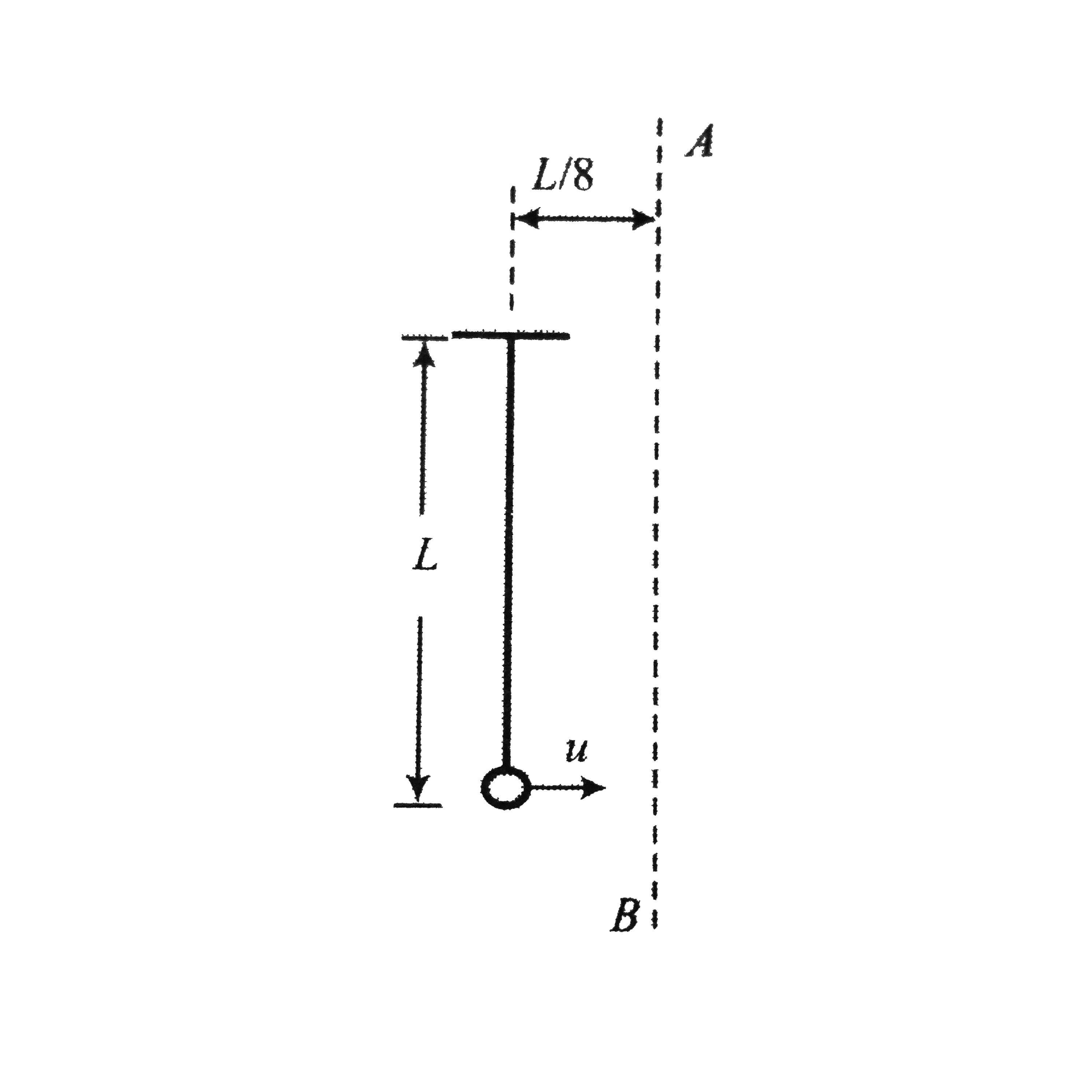
A particle is suspended vertically from a point O by an inextensible massless string of length L. A vertical line AB is at a distance L/8 from O as shown in figure. A horizontal velocity u is imparted to tha particle. At horizontal velocity u is imparted to the particle. At some point, its motion ceases to be circular and eventually the object passes through line AB. At the instant of crossing AN, its velocity is horizontal. Find out the value of u.
The correct Answer is:4
It is clear from the statement of the problem that the particle leaves the circular path before it crosses the line AB second time, during its upward motion.
Let us assume that the particle leaves the circular path at ‘P’ and v is the velocity of the particle at P. Then, conservation of mechanical energy at P and at the lowest point yields :
12mu2=12mv2+mgL(1+sinθ) ....(i)
At point P:T=mgsinθ=mv2L. If T becomes zero. v2=gLsinθ .....(ii)
After leaving the circular path, the particle moves along a parabolic trajectory as a projectile.
As it is given that velocity of the particle when it crosses AB is horizontal, it is clear that, when it is crossing AB, it is passing through its highest point in the parabolic path.
⇒12×Range=Lcosθ−L8
v2sin2(90−θ)2g=Lcosθ−L8 ....(iii)
From (ii) and (iii), cosθ=12⇒θ=60∘
Using this in (i) , we get
u=
⎷[4+3√32gL]

Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS5videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - ASSERTION & REASON TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)53videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
A particle is suspended vertically from a point O by an inextensible mass less string of length L. A vertical line AB is at a distance of L8 from O as shown in figure. The particle is given a horizontal velocity u. At some point, its motion ceases to be circular and eventually the object passes through the line AB. At the instant of crossing AB, its velocity is horizontal. Find u.
 View Solution
View SolutionA particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
View SolutionA particle is projected with velocity V for point O of particle makes 10 revolutions before coming out. Find l.
 View Solution
View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
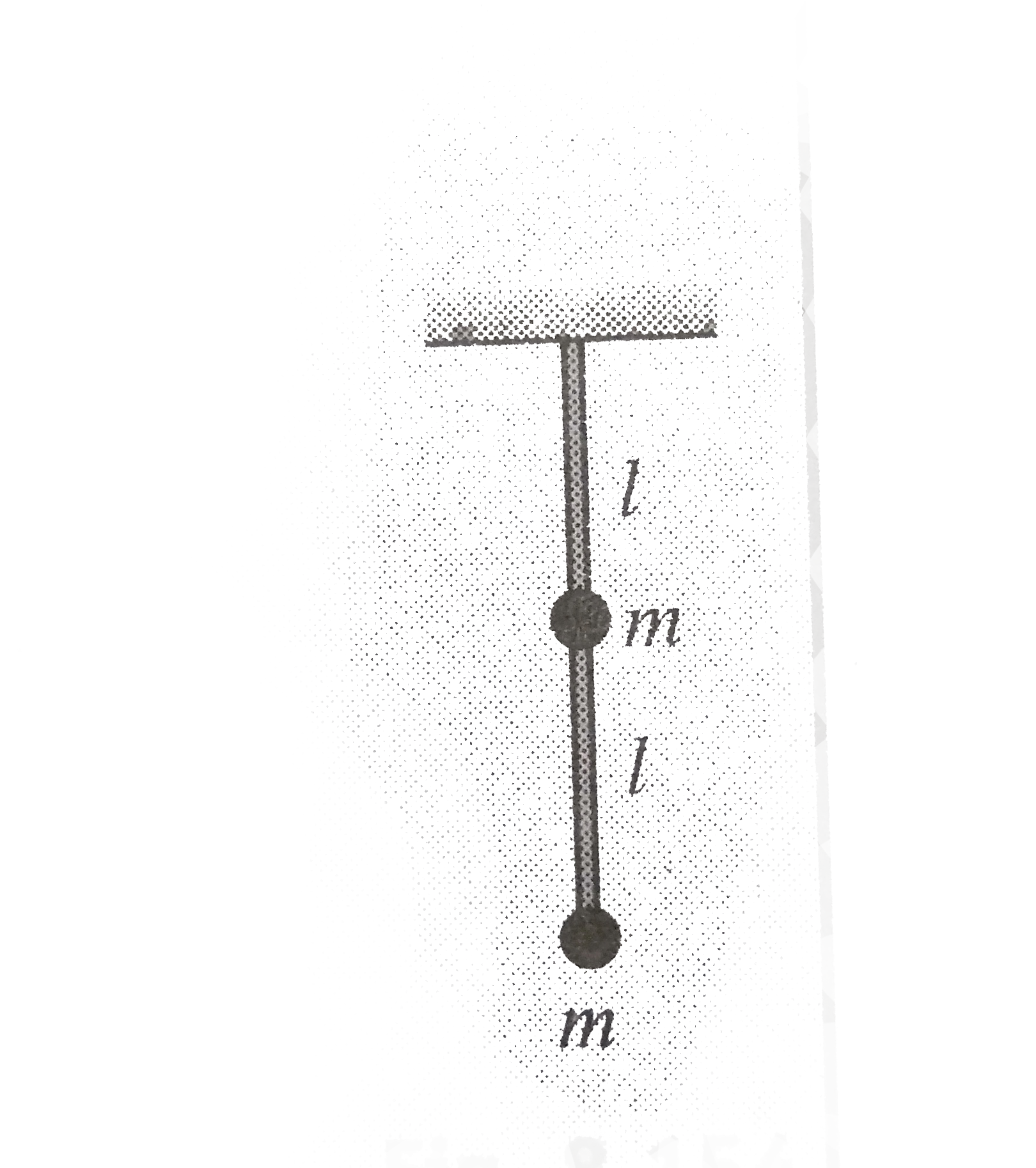 View Solution
View SolutionA sphere is suspended by a thread of length l. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
View SolutionA particle is dropped from a height h. Another particle which is initially at a horizontal distance d from the first is simultaneously projected with a horizontal velocity u and the two particles just collide on the ground. Then
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
 View Solution
View SolutionA horizontal plane supports a fixed vertical cylinder of radius R and a particle is attached to the cylinder by a horizontal thread AB as shown in Fig. The particle initially rest on a horizontal plane. A horizontal velocity v0 is imparted to the particle, normal to the threading during subsequent motion. Point out the false statements:
 View Solution
View SolutionA particle suspended from a fixed point, by a light inextensible thread of length L is projected horizontally from its lowest position with velocity 7gL . The thread will slack after swinging through an angle , such that equal
View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.
 View Solution
View Solution

