Two blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]
![Two blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m//s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m//s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M. [Take sintheta=tantheta=0.05 and g=10m//s^2]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V02_CH11_E01_193_Q01.png)
The correct Answer is:0.84, 15 kg
Considering the motion of block of mass m from A to B. Acceleration of the block.
a=−[mgsinθ+fm]=−[mgsinθ+μmgcosθm]
Here
cosθ=√1−sin2θ=√1−(0.05)2=0.99=1
a=−[gsinθ+μgcosθ]=−[sinθ+μcosθ)g
=−10[0.05+0.25×1]−3m/s2
Let velocity of block A just before collision is v1.
Using v2−u2=2as
v21=(10)2+2(−3)×6⇒v1=8m/s
Now considering situation just after collision
Let v2 be the velocity of mass m after collision and v3 be the velocity of mass M after collision.
The block of mass M moves from B to C (distance 0.5 m) and comes to rest. Now considering the motion of M from B to C. Again using v2−u2=2as
Here u=v3,v=0 and acceleration a=–3m/s2
(here acceleration of M is same as a previous case because all other parameters are the same)
Hence (0)2−v23=2(−3)×0.5⇒v3=√3=1.73m/s
The block of mass m moves from B to A after collision
Using W.E. theorem
Wtotal=ΔK=Wfriction+Wgravity=KA−KB
=(μmgcosθ)s+mgh=12mv2−12mv22
Here s = 6m, h = 0.3 m and v = 1 m/s
Substituting the value in above equation
We get v2=¬5m/s ∴ Coefficient of restitution
e=∣∣∣Relative velocity of seperationRelative velocity of approach∣∣∣=∣∣∣5+1.738−0∣∣∣=0.84
Now for calculating mass apply conservation of linear momentum before and after collision
mv1=Mv3−mv2,M=m(v1+v2)v3=2(8+5)1.73=15.02kg.

Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS5videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - ASSERTION & REASON TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)53videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 N - Question 2 - Select One
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N - Question 3 - Select One
Two blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
Two identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
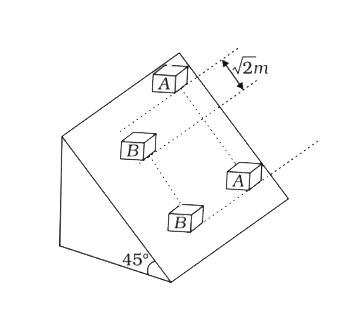 View Solution
View SolutionFind the force required to pull a block of mass 100kg up an incline of 8∘ at a uniform speed of 5m/s. The coefficient of friction between the block and the plane is 0.3.
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View Solution

