A liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is
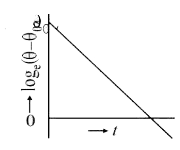


The correct Answer is:A
According to Newton’s law of cooling
dθdt≡k(θ−θ0)
∫dθθ−θ0=−k∫dt
In (θ−θ0)=−kt+C
So graph is straight line.

Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced(Archive) Level - 21videos
PROPERTIES OF MATTER
- BOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 229videos
PROPERTIES OF MATTER
- BOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -250videos
PROPERTIES OF MATTER
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K10videos
MOVING CHARGES & MAGNETISM
- BOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS30videos
QUIZ
Similar Questions
In Newton's law of cooling dθdt=−k(θ−θ0) the constant k is proportional to .
View SolutionTwo liquids of specific heat ratio 1:2 are at temperature 2θandθ
View SolutionThe correct graph between the temperature of a hot body kept in cooler surrounding and time is (Assume newton's law of cooling)
View SolutionThe temperature of water in calorimeter is θ and the temperature of surrounding is θ0(<θ). Observation are recorded for temperature difference (θ−θ0) and time t. The cooling curve is best represented in graph.
View SolutionThemperature of a body θ is slightly more than the temperature of the surrounding θ0 its rate of cooling (R) versus temperature of body (θ) is plotted its shape would be .
View SolutionEvaluate: ∫√tanθ dθ
View SolutionTwo bodies A and B of equal masses, area and emissivity cooling under Newton's law of cooling from same temperature are represented by the graph: If θ is the instantaneous temperature of the body and θ0, is the temperature of surroundings, then relationship between their specific heats is
View SolutionInstantaneous temperature difference between cooling body and the surroundings obeying Newton's law of cooling is θ. Which of the following represents the variation of In θ with time t?
View SolutionA body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newton's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
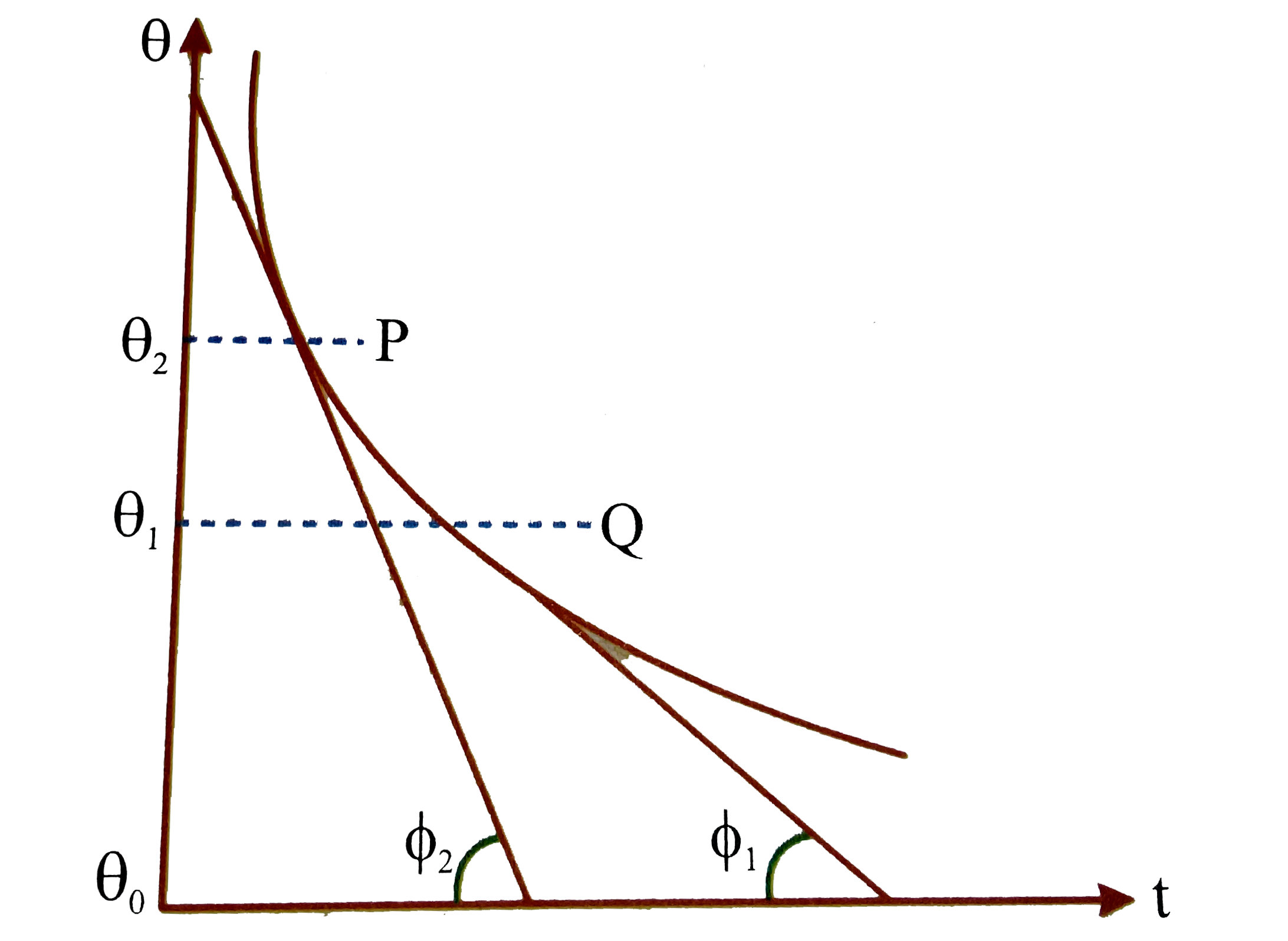 View Solution
View SolutionIf the system were lossing heat according to Newton's cooling law the temperature of the mixture would change with time according to (while heater was on) .
View Solution

