The area of the plates of a capacitor is 50cm2 each and the separation between them is 1mm. The space between the plates is filled with a material of dielectric constant 4. the capacitor, initially uncharged, is connected to a battery of EMF 50 V. the work done by the battery until the capacitor gets completely charged is (in μJ).
0.22
0.44
0.88
1.76
The correct Answer is:C
To solve the problem step by step, we need to calculate the capacitance of the capacitor and then determine the work done by the battery when charging the capacitor. Here’s how to do it:
Step 1: Convert the given values to standard units
- Area A=50cm2=50×10−4m2=5×10−3m2
- Separation d=1mm=1×10−3m
- Dielectric constant K=4
- EMF of the battery V=50V
Hint for Step 1: Always convert units to SI units for consistency in calculations.
Step 2: Calculate the capacitance C
The formula for the capacitance of a parallel plate capacitor filled with a dielectric is given by:
C=Kϵ0Ad
Where:
- ϵ0=8.85×10−12F/m (permittivity of free space)
Substituting the values:
C=4×(8.85×10−12)×(5×10−3)1×10−3
Calculating this gives:
C=4×8.85×5×10−151×10−3=4×8.85×5×10−12=1.77×10−11F
Step 3: Calculate the work done W
The work done by the battery in charging the capacitor is given by:
W=12CV2
Substituting the values of C and V:
W=12×(1.77×10−11)×(50)2
Calculating this gives:
W=12×(1.77×10−11)×2500=2.2125×10−8J
Step 4: Convert work done to microjoules
To convert joules to microjoules:
W=2.2125×10−8J=22.125μJ
Final Answer
The work done by the battery until the capacitor gets completely charged is approximately 22.125μJ.
---
- Area A=50cm2=50×10−4m2=5×10−3m2
- Separation d=1mm=1×10−3m
- Dielectric constant K=4
- EMF of the battery V=50V
The formula for the capacitance of a parallel plate capacitor filled with a dielectric is given by:
- ϵ0=8.85×10−12F/m (permittivity of free space)
The work done by the battery in charging the capacitor is given by:
To convert joules to microjoules:
The work done by the battery until the capacitor gets completely charged is approximately 22.125μJ.
Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - LEVEL 2
40 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Main (Archive) LEVEL-1
36 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - LEVEL 0 (LONG ANSWER TYPE)
3 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
The capacitance of a parallel plate capacitor is C when the region between the plate has air. This region is now filled with a dielectric slab of dielectric constant k. The capacitor is connected to a cell of emfE, and the slab is taken out
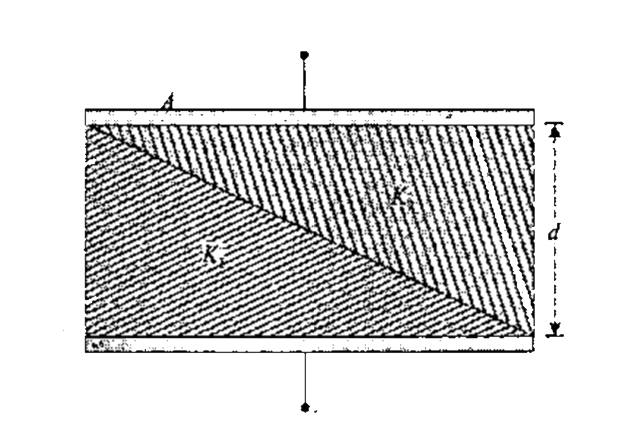
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
View SolutionA 2μF capacitor that was initially uncharged is connected to a battery of EMF 100V and a resistance and the switch is closed. The heat generated in the resistance until the capacitor becomes fully charged is (in mJ):
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionConsider a disconnected plate capacitor of capacity 10μF with air filled in the gap between the plates. Now one-half of the space between the plates is filled with a dielectric of dielectric constant 4 as shown in .The capacity of the capacitor changes to
 .
.
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionA parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
View SolutionA capacitor is connected to a battery. The force of attraction between the plates when the separation between them is halved.
View SolutionAn LR circuit with a battery connected at t =0. Which of the following quantities will be zero just after the connection?
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View Solution